Непозиционные и позиционные системы счисления
Докажем существование представления любого натурального числа в виде
Системы счисления с другими основаниями, их происхождение и применение
Умножение и деление
Перевод чисел из одной системы счисления в другую
ИСПОЛЬЗОВАНИЕ СИСТЕМ СЧИСЛЕНИЯ В КОМПЬЮТЕРНОЙ ТЕХНИКЕ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЯХ
Способы построения двоичных кодов
Навигация
Перевод чисел из одной системы счисления в другую
Системы счисления и основы двоичных кодировок
54749
знаков
16
таблиц
10
изображений
1.6 Перевод чисел из одной системы счисления в другую
Существует много различных способов перевода чисел из одной системы счисления в другую.
Способ деления.
Пусть дано число N=anan-1. . . a1 а0р.
Для получения записи числа N в системе с основанием h следует представить его в виде:
N=bmhm+bm-1hm-1+... +b1h+b0 (1)
где 1<bm<h-1, 0 ≤ bi ≤ h-l (i=0, 1,... ,m-l), тогда
N=bmbm-1... b1boh (2)
Из (1) получаем:
N= (bmhm-1+...+b)*h +b0 = N1h+b0, где 0≤ b0 ≤h (3)
To есть цифра b0 является остатком от деления числа N на число h. Неполное частное Nl= bmhm-1+ . . . +b1 представим в виде:
Nl= (bmhm-2 + ... + b2)h + b1 = N2h+b1, где 0≤ b2 ≤h (4)
Таким образом, цифра bi в записи (2) числа N является остатком от деления первого неполного частного N1 на основание h новой системы счисления. Второе неполное частное N2 представим в виде:
N2 = (bmhm-3+ ... +b3)h+b2, где 0≤ b2 ≤h (5)
то есть цифра b2 является остатком от деления второго неполного частного N2 на основание h новой системы. Так как не полные частные убывают, то этот процесс конечен. И тогда мы получаем Nm= bm, где bm<h, так как:
Nm-1 = bmh+bm.1 = Nmh+bm.1
Таким образом, последовательность цифр bm, bm-1 . . ,b1,b0 в записи числа N в системе счисления с основанием h есть последовательность остатков последовательного деления числа N на основание h, взятая в обратной последовательности.
Рассмотрим пример: Выполнить перевод числа 123 в шестнадцатеричную систему счисления:
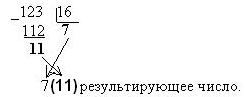
Таким образом, число 12310=7(11)16 либо можно записать как 7B16
Запишем число 340227 в пятеричной системе счисления:
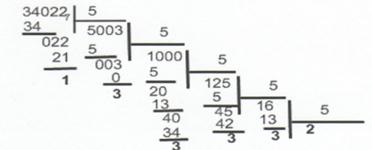
Таким образом, получаем, что 340227=2333315
Перевод с использованием десятичной системы счисления.
Любое число в любой системе счисления представимо в виде:
N = anpn+...+a1p+a0
Таким образом, имея запись числа в таком виде, мы легко можем перевести его в привычную нам десятичную систему счисления. Например
22095=2*53+2*52+0*51+9*50=30910
Так же, число, представленное в десятичной системе счисления, мы можем расписать по степеням любого другого основания:
2208097=2*75+2*74+0*73+8*72+0*71+9*70=388177
Таким способом можно перевести числа из одной системы в другую. Например: переведем число 6257 в 3-ичную систему счисления.
6257=6*72+2*71+5*70=6*49+2*7+5=31310
31310=1*35+0*34+2*33+1*32+2*31+1*30=1*243+2*27+1*9+2*3+1=1021203
Ответ: 625т=1021203
Систематические дроби. Перевод дробей в различные системы счисления.
Известно, что десятичная дробь отличается от целого числа только наличием запятой, отделяющей целую часть от дробной, и такое сходство не случайно.
Можно сказать, что запись дробного числа в виде десятичной дроби представляет собой перенесение общего принципа записи чисел в позиционной десятичной системе счисления на дробные числа.
В самом общем случае смешанное число, содержащее целую и дробную части, представляется в виде суммы степеней десятки и
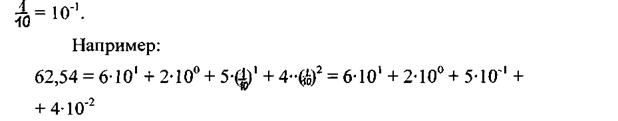
Десятичные дроби являются частным случаем систематических дробей, которые можно строить аналогичным образом для любой позиционной системы счисления.
Например, дробь 5-1 + 6-2 + 3-3 назвать восьмеричной и записать в виде: 0,5638.
Правила арифметических действий над ρ - ичными дробями (основание системы - q) такие же, как и над десятичными, но при действиях с однозначными числами нужно пользоваться таблицами сложения и умножения для данной системы.
Следует заметить, что не всякая простая дробь может быть записана в виде конечной десятичной дроби. Это явление наблюдается и в других позиционных системах счисления. При этом одно и то же число может в одной системе счисления записываться в виде конечной дроби, а в другой - в виде бесконечной.
Например:
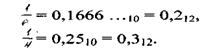
При переводе дробей из одной позиционной системы счисления в другую необходимо иметь в виду возможность получения бесконечных дробей.
Общее правило перевода числа в систему счисления с основанием n:
Для перевода целого числа в систему счисления с основанием n его надо последовательно делить на n (отбрасывая остатки), при переводе дроби, меньшей единицы – последовательно умножить на n (отбрасывая целые). Цифрами числа в n – ичной системе счисления в первом случае будут остатки, записанные в обратном порядке, а во втором – целые части, записанные в порядке их получения. Целые и дробные части в смешанном числе переводятся отдельно.
Пример: 378,835937510 перевести в систему счисления с основанием q=8
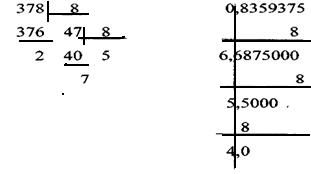
Итак, 378,835937510=572,6548
Быстрый перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно.
Перевод чисел между системами счисления, основания которых являются степенями числа 2, может производиться более простым алгоритмом.
Для записи двоичных чисел используют две цифры, то есть в каждом разряде числа возможны два варианта записи. Для записи восьмеричных чисел используется восемь цифр, то есть возможны восемь вариантов. А для записи шестнадцатеричных чисел используется 16 цифр, то есть 16 возможных вариантов.
Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то нужно его дополнить нулями слева.
Пример:
100 101 000 0102
4 5 0 28
111 111 101 000 010 000 1002
7 7 5 0 2 0 48
А для перевода целого двоичного числа в шестнадцатеричное, число разбивают на группы по 4 цифры и следуют тому же алгоритму, что и с
восьмеричной системой счисления.
Например:
1001 0000 1100 0111 00012
9 0 С 7 116
Например:
1111 1001 1101 0002
F 9 D 016
Данное правило работает и наоборот, то есть любое целое число можно перевести из восьмеричной в двоичную и из шестнадцатеричной в двоичную.
Например:
| 1 | 2 | 3 | 4 | 5 | 6 | 78 |
| 001 | 010 | 011 | 100 | 101 | 110 | 1112 |
| А | B | C | D | E | F | 1 | 2 | 3 | 4 | 5 |
| 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 0001 | 0010 | 0011 | 0100 | 0101 |
| 6 | 7 | 8 | 916 |
| 0110 | 0111 | 1000 | 10012 |
Похожие работы
... также невысока и обычно составляет около 100 кбайт/с. НКМЛ могут использовать локальные интерфейсы SCSI. Лекция 3. Программное обеспечение ПЭВМ 3.1 Общая характеристика и состав программного обеспечения 3.1.1 Состав и назначение программного обеспечения Процесс взаимодействия человека с компьютером организуется устройством управления в соответствии с той программой, которую пользователь ...
... . В случае выбора пункта «выход», необходимо реализовать завершение работы программы и передачу управления операционной системе DOS. 1.3. Требования техническим и программным средствам Программа выполнена на языке ассемблера 8086 процессора, соответственно ей необходим IBM PC – совместимый компьютер с процессором не ниже 8086, также программа может выполняться на компьютерах с ...
... в широкую практику разработки программ объектно-ориентированного программирования, впитавшего в себя идеи структурного и модульного программирования, структурное программирование стало фактом истории информатики. Билет № 9 Текстовый редактор, назначение и основные функции. Для работы с текстами на компьютере используются программные средства, называемые текстовыми редакторами или текстовыми ...
... можно изобразить отдельно. Формирователь выхода «Равенство кодов» Формирователь выхода «Больше» Формирователь выхода «Меньше». Арифметические устройства Другой класс приборов, используемых в дискретной технике предназначен для выполнения арифметических действий с двоичными числами: сложения, вычитания, умножения, деления. К арифметическим устройствам относятся также схемы, ...
0 комментариев