Навигация
Частные производные первого порядка. Полный дифференциал
11164
знака
0
таблиц
0
изображений
3. Частные производные первого порядка. Полный дифференциал
Пусть задана функция двух переменных 
. Дадим аргументу 
приращение 
, а аргумент 
оставим неизменным. Тогда функция 
получит приращение 
, которое называется частным приращением по переменной и обозначается 
:
.
Аналогично, фиксируя аргумент и придавая аргументу прираще-ние 
, получим частное приращение функции по переменной :
.
Величина 
называется полным прира-щениием функции в точке 
.
Определение 4. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю (если этот предел существует). Обозначается частная производная так: 
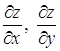или 
, или 
.
Таким образом, по определению имеем:
,
.
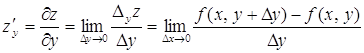Частные производные функции вычисляются по тем же правилам и формулам, что и функция одной переменной, при этом учитывается, что при дифференцировании по переменной , считается постоянной, а при дифференцировании по переменной постоянной считается .
Пример 3. Найти частные производные функций:
а) 
; б)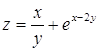 
.
Решение. а) Чтобы найти 
считаем постоянной величиной и дифференцируем как функцию одной переменной :
.
Аналогично, считая постоянной величиной, находим 
:
.
Решение.
б)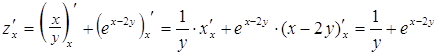 
;
.
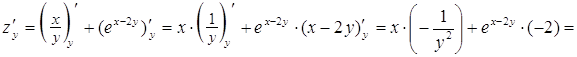
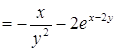Определение 5. Полным дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.
.
Учитывая, что дифференциалы независимых переменных совпадают с их приращениями, т.е. 
, формулу полного дифференциала можно записать в виде
или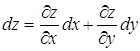 
.
Пример 4. Найти полный дифференциал функции 
.
Решение. Так как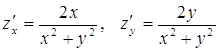 
, то по формуле полного дифференциала находим
.
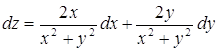Похожие работы
... и градиент функции вычисляется в меньшем числе точек. Описание программы Программа предназначена для нахождения точек минимума функций нескольких переменных – другими словами для минимизации этих функций. В программе реализован один из методов спуска – Градиентный метод спуска с выбором шага. Начальный шаг задается. Изменение шага осуществляется по схеме если ; если Вычисление ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... векторы в силу (6.8) оказались бы линейно зависимыми .Разделив обе части на 0 получим равенство вида (6.9). ч.т.д. Пример №5. Пусть требуется найти экстремум функции u=xyzt при условии x+y+z+t=4c; область изменения переменных определяетссся неравенствовами x>0, y>0, t>0, z>0. Применяя к этой задаче метод Лагранжа, введем вспомогательную ...
0 комментариев