Навигация
Для определения критических точек решаем систему уравнений
11164
знака
0
таблиц
0
изображений
2. Для определения критических точек решаем систему уравнений
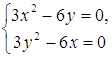или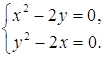 
Из первого уравнения системы находим: 
. Подставляя найденное значение y во второе уравнение, получим
, 
, 
,
откуда
.
Находим значения y, соответствующие значениям 
. Подставляя значения в уравнение , получим: 
.
Таким образом, имеем две критические точки: 
и 
.
3. Находим частные производные второго порядка:
; 
; 
.
4. Вычисляем значения частных производных второго порядка в каждой критической точке. Для точки имеем:
, 
, 
.
Так как
,
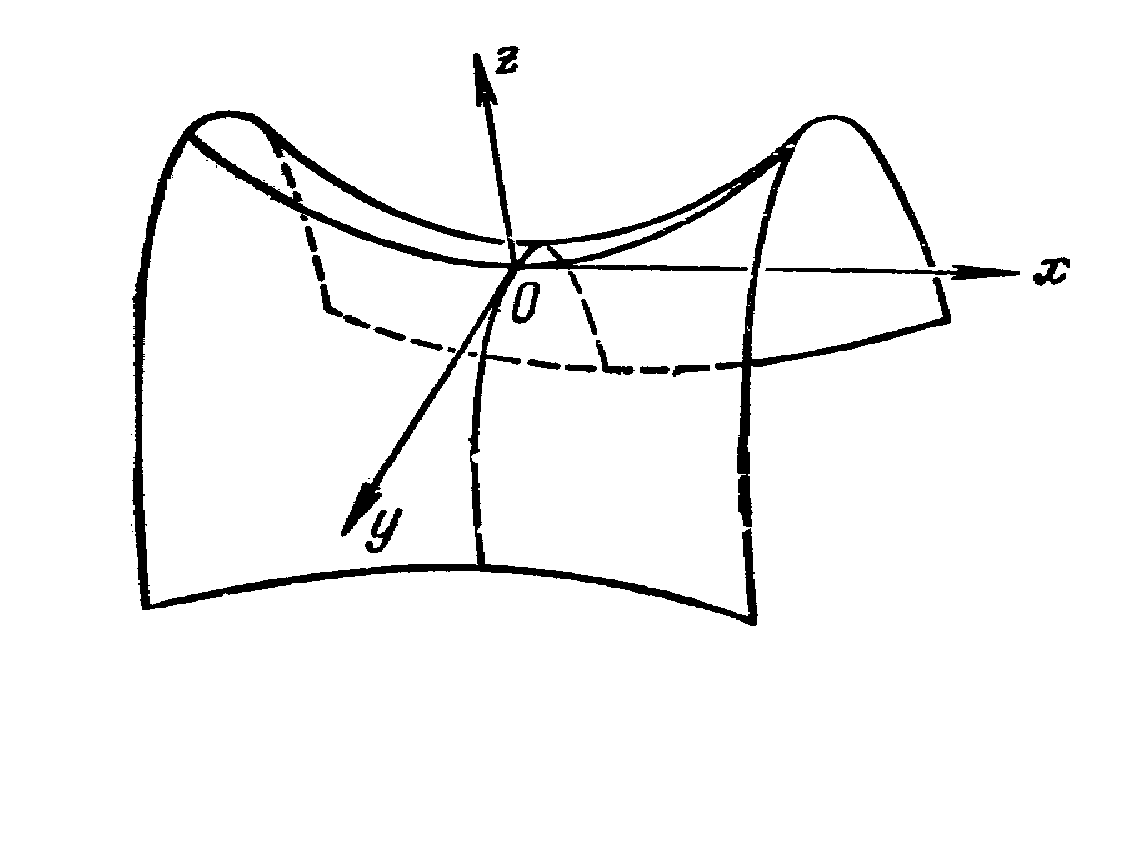
то в точке 
экстремума нет.
В точке :
, 
, 
и, следовательно,
.
Значит, в силу достаточного условия экстремума, в точке 
функция имеет минимум, так как в этой точке 
и 
.
5. Находим значение функции в точке :
.
6. Условный экстремум
В теории функций нескольких переменных иногда возникают задачи, когда экстремум функции нескольких переменных необходимо найти не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
Пусть 
– функция двух переменных, аргументы x и y которой удовлетворяют условию 
, называемому уравнением связи.
Определение 8. Точка 
называется точкой условного минимума (максимума) функции , если существует такая окрестность точки 
, что для всех точек 
из этой окрестности, удовлетворяющих условию , выполняется неравенство 
, (
).
Если уравнение связи можно разрешить относительно одной из переменных (например, выразить y через x: 
), то задача отыскания условного экстремума функции двух переменных сводится к нахождению экстремума функции одной переменной. Для этого подставляют найденное значение в функцию двух переменных. В результате получают функцию одной переменной x: 
. Ее экстремум и будет условным экстремумом функции .
Замечание. В более сложных случаях, когда уравнение связи не разрешимо относительно одной из переменных, для отыскания условного экстремума используется метод множителей Лагранжа.
Пример 7. Найти экстремумы функции 
при условии, что ее аргументы удовлетворяют уравнению связи 
.
Решение. Из уравнения связи находим функцию 
и подставляем ее в функцию z. Получим функцию одной переменной
или
Находим экстремум данной функции:
, 
, 
– критическая точка первого рода (точка, подозрительная на экстремум). Так как 
, то в точке функция 
имеет локальный минимум. Из уравнения связи находим: 
. Следовательно, функция
в точке 
имеет условный минимум:
.
Литература
1. Белько И. В., Кузьмич К. К. Высшая математика для экономистов. I семестр: Экспресс-курс. – М.: Новое знание, 2002. – 140 с.
2. Гусак А. А.. Математический анализ и дифференциальные уравне-ния.– Мн.: ТетраСистемс, 1998. – 416 с.
3. Гусак А. А.. Высшая математика. Учебное пособие для студентов вузов в 2-х томах. – Мн., 1998. – 544 с. (1 т.), 448 с. (2 т.).
4. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Высшая математика для экономистов: Учебник для вузов / Под ред. проф. Н. Ш. Кремера.– М.: ЮНИТИ, 2002. – 471 с.
5. Яблонский А. И., Кузнецов А. В., Шилкина Е. И. и др. Высшая математика. Общий курс: Учебник / Под общ. ред. С. А. Самаля.– Мн.: Выш. шк., 2000. – 351 с.
Похожие работы
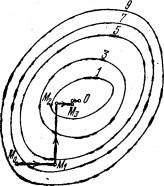
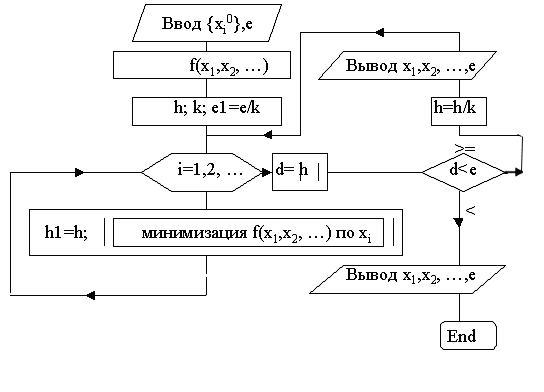
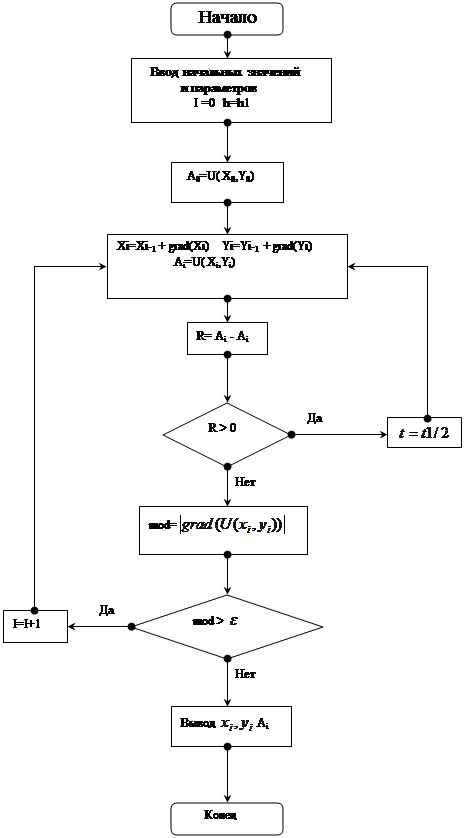
... и градиент функции вычисляется в меньшем числе точек. Описание программы Программа предназначена для нахождения точек минимума функций нескольких переменных – другими словами для минимизации этих функций. В программе реализован один из методов спуска – Градиентный метод спуска с выбором шага. Начальный шаг задается. Изменение шага осуществляется по схеме если ; если Вычисление ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... векторы в силу (6.8) оказались бы линейно зависимыми .Разделив обе части на 0 получим равенство вида (6.9). ч.т.д. Пример №5. Пусть требуется найти экстремум функции u=xyzt при условии x+y+z+t=4c; область изменения переменных определяетссся неравенствовами x>0, y>0, t>0, z>0. Применяя к этой задаче метод Лагранжа, введем вспомогательную ...
0 комментариев