Навигация
Частные производные высших порядков
11164
знака
0
таблиц
0
изображений
4. Частные производные высших порядков
Частные производные 
и 
называют частными производными первого порядка или первыми частными производными.
Определение 6. Частными производными второго порядка функции 
называются частные производные от частных производных первого порядка.
Частных производных второго порядка четыре. Они обозначаются следующим образом:
или 
; 
ил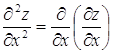и 
;
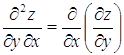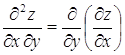или 
; 
или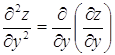 
.
Аналогично определяются частные производные 3-го, 4-го и более высоких порядков. Например, для функции имеем:
, 
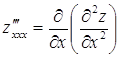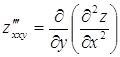и т. д.
Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными. Для функции таковыми являются производные 
. Заметим, что в случае, когда смешанные производные непрерывны, то имеет место равенство 
.
Пример 5. Найти частные производные второго порядка функции
.
Решение. Частные производные первого порядка для данной функции найдены в примере 3:
Дифференцируя и по переменным х и y, получим
,
;
;
.
5. Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
Определение 7. Точка 
называется точкой минимума (максимума) функции , если существует такая окрестность точки 
, что для всех точек 
из этой окрестности выполняется неравенство 
, (
).
Точки минимума и максимума функции называются точками экстремума, а значения функции в этих точках – экстремумами функции (минимумом и максимумом соответственно).
Заметим, что минимум и максимум функции имеют локальный характер, так как значение функции в точке сравнивается с ее значениями в точках, достаточно близких к .
Теорема 1 (необходимые условия экстремума). Если 
– точка экстремума дифференцируемой функции , то ее частные производные и 
в этой точке равны нулю: 
.
Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция может иметь экстремум, а может и не иметь.
Теорема 2 (достаточное условие экстремума). Пусть функция : а) определена в некоторой окрестности критической точки , в которой 
и ; б) имеет непрерывные частные производные второго порядка 
. Тогда, если 
, то функция 
в точке имеет экстремум: максимум, если А<0; минимум, если А>0; если 
, то функция в точке экстремума не имеет. В случае 
вопрос о наличии экстремума остается открытым.
При исследовании функции двух переменных на экстремум рекомендуется использовать следующую схему:
1. Найти частные производные первого порядка: и .
2. Решить систему уравнений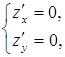 
и найти критические точки функции.
3. Найти частные производные второго порядка: 
, 
, 
.
4. Вычислить значения частных производных второго порядка в каждой критической точке и, используя достаточные условия, сделать вывод о наличии экстремума.
5. Найти экстремумы функции.
Пример 6. Найти экстремумы функции 
.
Решение. 1. Находим частные производные и :
, 
.
Похожие работы
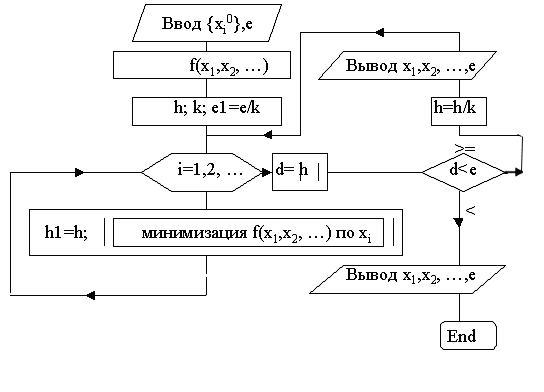
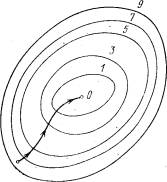
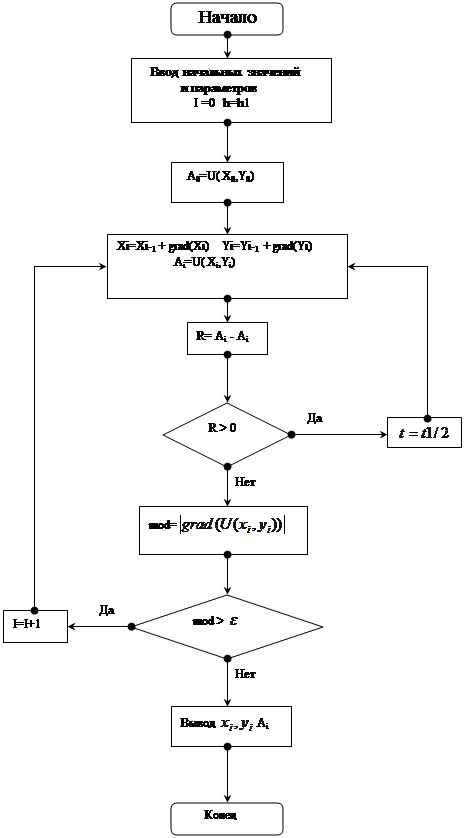
... и градиент функции вычисляется в меньшем числе точек. Описание программы Программа предназначена для нахождения точек минимума функций нескольких переменных – другими словами для минимизации этих функций. В программе реализован один из методов спуска – Градиентный метод спуска с выбором шага. Начальный шаг задается. Изменение шага осуществляется по схеме если ; если Вычисление ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
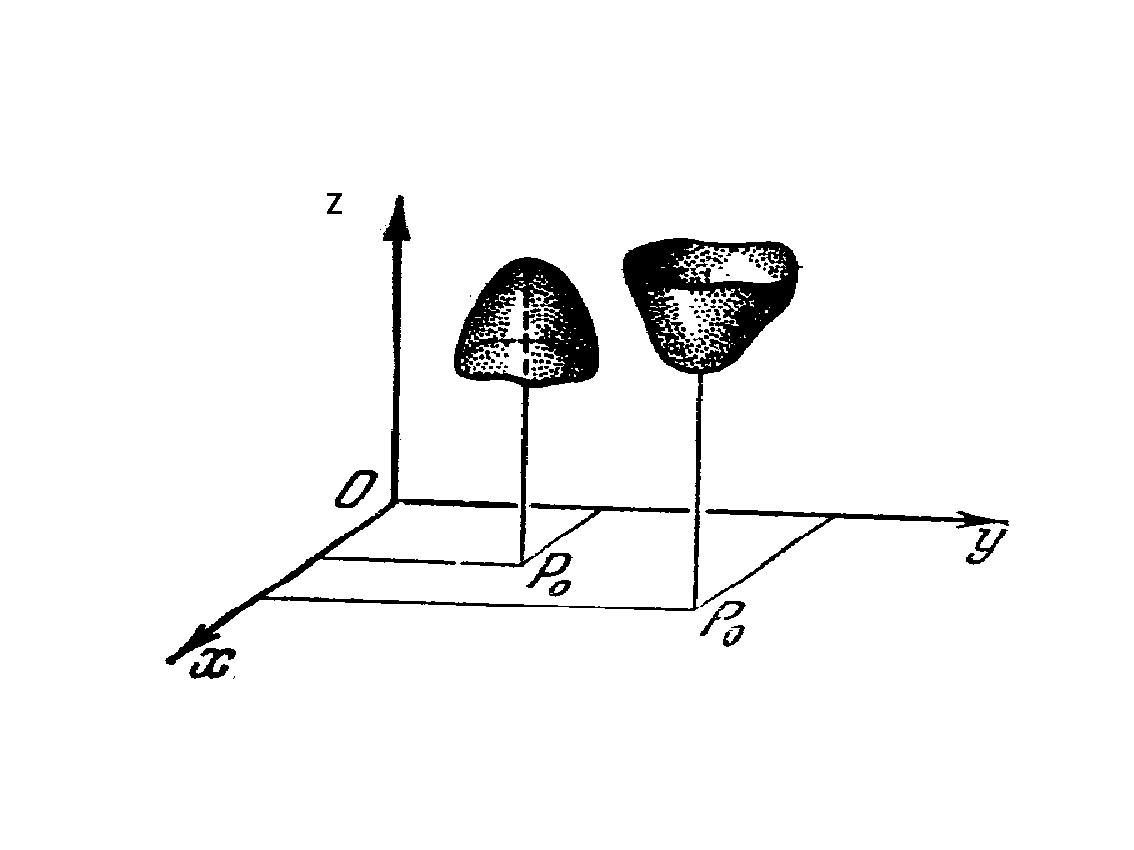
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... векторы в силу (6.8) оказались бы линейно зависимыми .Разделив обе части на 0 получим равенство вида (6.9). ч.т.д. Пример №5. Пусть требуется найти экстремум функции u=xyzt при условии x+y+z+t=4c; область изменения переменных определяетссся неравенствовами x>0, y>0, t>0, z>0. Применяя к этой задаче метод Лагранжа, введем вспомогательную ...
0 комментариев