Метризуемость топологических пространств

Министерство образования и науки Российской Федерации

Вятский государственный гуманитарный университет

Математический факультет

Кафедра математического анализа и МПМ

Дипломная работа

Метризуемость топологических пространств

Выполнила

студентка 5 курса

математического факультета

Побединская Татьяна Викторовна

_______________________________

(подпись)

Научный руководитель

к.ф.-м.н., доцент кафедры математического анализа и МПМ Варанкина Вера Ивановна

_______________________________

(подпись)

Рецензент

_______________________________

(подпись)

Допущена к защите в ГАК

Зав. кафедрой______________________________к.п.н., доцент Крутихина М.В.

(подпись)

«_____» _______________2004 г.

Декан факультета_________________________к.ф.-м.н., доцент Варанкина В.И.

(подпись)

«_____» _______________2004 г.

КИРОВ

2004

Содержание

Введение. 3

Глава I. Основные понятия и теоремы.. 4

Глава II. Свойства метризуемых пространств. 10

Глава III. Примеры метризуемых и неметризуемых пространств. 21

Библиографический список. 24

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Тема дипломной работы – «Метризуемость топологических пространств».

В первой главе работы вводятся основные определения, связанные с понятиями метрического и топологического пространств.

Во второй главе рассматриваются и доказываются следующие свойства метризуемых пространств:

1. Метризуемое  пространство хаусдорфово.

2. Метризуемое  пространство нормально.

3. В метризуемом пространстве выполняется первая аксиома счетности.

4. Метризуемое пространство совершенно нормально.

5. Для метризуемого пространства  следующие условия эквивалентны:

1)  сепарабельно,

2)  имеет счетную базу,

3)  финально компактно.

6. Любое метризуемое топологическое пространство может быть метризовано ограниченной метрикой.

7. Произведение счетного числа метризуемых пространств метризуемо.

В третьей главе рассматриваются примеры метризуемых и неметризуемых пространств.

 

 

 

 

Глава I. Основные понятия и теоремы

Определение. Метрическим пространством называется пара , состоящая из некоторого множества (пространства)  элементов (точек) и расстояния, то есть однозначной неотрицательной действительной функции , определенной для любых  и  из и удовлетворяющей трем условиям:

1)      (аксиома тождества);

2)    (аксиома симметрии);

3)    (аксиома треугольника).

Определение. Пусть – некоторое множество. Топологией в  называется любая система  его подмножеств , удовлетворяющая двум требованиям:

1.   Само множество  и пустое множество принадлежат .

2.   Объединение  любого (конечного или бесконечного) и пересечение  любого конечного числа множеств из  принадлежат .

Множество с заданной в нем топологией , то есть пара , называется топологическим пространством.

Множества, принадлежащие системе , называются открытыми.

Множества , дополнительные к открытым, называются замкнутыми множествами топологического пространства .

Определение. Совокупность  открытых множеств топологического пространства называется базой топологического пространства , если всякое открытое множество в  может быть представлено как объединение некоторого числа множеств из .

Теорема 1. Всякая база  в топологическом пространстве обладает следующими двумя свойствами:

1)   любая точка содержится хотя бы в одном ;

2)   если  содержится в пересечении двух множеств  и из , то существует такое , что .

 

Определение. Открытым шаром или окрестностью точки  радиуса   в метрическом пространстве  называется совокупность точек , удовлетворяющих условию . При этом  – центр шара,  – радиус шара.

Утверждение 1. Для любого , принадлежащего -окрестности точки , существует окрестность радиуса , включенная в -окрестность точки .

Доказательство. Выберем в качестве  :.

Достаточно доказать для произвольного  импликацию . Действительно, если , то

Получаем, что , что и требовалось доказать.

Теорема 2. Совокупность всех открытых шаров образуют базу некоторой топологии.

Доказательство. Проверим свойства базы (теорема 1).

·     Свойство первое очевидно, так как для любого выполняется  для любого .

·     Проверим второе свойство.

Пусть ,  и , тогда, воспользовавшись утверждением 1, найдем такое , что  Теорема доказана.

 

Определение. Топологическое пространство  метризуемо, если существует такая метрика  на множестве , что порожденная этой метрикой топология совпадает с исходной топологией пространства .

Аксиомы отделимости

 

Аксиома . Для любых двух различных точек топологического пространства окрестность хотя бы одной из них не содержит другую.  

 

Аксиома . Каждая из двух произвольных точек пространства имеет окрестность, не содержащую вторую точку.

Предложение.  является - пространством тогда и только тогда, когда для любого множество  замкнуто.

Доказательство.

Необходимость. Пусть . Так как  является -пространством, то существует окрестность , не содержащая .

Рассмотрим

Докажем, что . Применим метод двойного включения:

·     Очевидно, что  по построению множества .

·     .

Пусть  отсюда для любого  отличного от  существует окрестность , значит , тогда .

Множество - открыто, как объединение открытых множеств.

Тогда множество - замкнуто, как дополнение открытого множества.

Достаточность. Рассмотрим . По условию замкнутые множества. Так как , то . Множество -открыто как дополнение замкнутого и не содержит . Аналогично доказывается существование окрестности точки , не содержащей точку

Что и требовалось доказать.

 Аксиома  ( аксиома Хаусдорфа). Любые две точки пространства имеют непересекающиеся окрестности.

 Аксиома . Любая точка и не содержащее ее замкнутое множество имеют непересекающиеся окрестности.

Определение. Пространства, удовлетворяющие аксиомам  () называются -пространствами (-пространства называют также хаусдорфовыми пространствами).

Определение. Пространство называется нормальным или -пространством, если оно удовлетворяет аксиоме , и всякие его два непустые непересекающиеся замкнутые множества имеют непересекающиеся окрестности.

Определение. Система окрестностей называется определяющей системой окрестностей точки , если для любой окрестности  точки  найдется окрестность из этой системы, содержащаяся в .

Определение. Если точка  топологического пространства имеет счетную определяющую систему окрестностей, то говорят, что в этой точке выполняется первая аксиома счетности. Если это верно для каждой точки пространства, то пространство называется пространством с первой аксиомой счетности.

 

Определение. Две метрики  и  на множестве  называются эквивалентными, если они порождают на нем одну и ту же топологию.

Пример. На плоскости  для точек  и  определим расстояние тремя различными способами:

1. ,

2. ,

3. .

·     Введенные расстояния являются метриками. Проверим выполнимость аксиом метрики для введенных расстояний.

1. 1)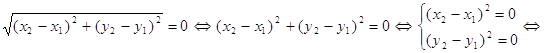

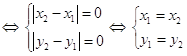
2) так как  и , то вторая аксиома очевидна:

3) рассмотрим точки ,, и докажем следующее неравенство:

 

Возведем это неравенство в квадрат:

.

Так как  и  (поскольку ) и выражение  есть величина неотрицательная, то неравенство  является верным.

2. 1)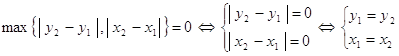

2) так как  и , то вторая аксиома очевидна: .

3) рассмотрим точки ,, и докажем следующее неравенство: .

Тогда и .

3. 1)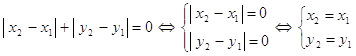

2) так как  и , то вторая аксиома очевидна:

.

3) рассмотрим точки ,,.

Неравенство:  - очевидно.

·     Введенные метрики  и  эквивалентны, то есть задают одну и ту же топологию.

Пусть метрика  порождает топологию , - топологию  и - топологию . Достаточно показать два равенства.

Покажем, что .

Рассмотрим множество,  открытое в  и покажем, что  открыто в . Возьмем некоторую точку и изобразим шар с центром в этой точке, который целиком лежит в . Шар в - квадрат, шар в - круг. А квадрат всегда можно заключить в круг. Тогда  открыто и в .

Аналогично доказывается, что . А тогда и .

 

Глава II. Свойства метризуемых пространств

 

Свойство 1. Метризуемое пространство хаусдорфово.

Доказательство. Пусть . Возьмем . Докажем, что .

Предположим, что , тогда существует , т.е.  и . Тогда, . Получили противоречие. Следовательно, .

Следствие. Метризуемое пространство является  - пространством.

Определение. Расстоянием от точки  до множества  в метрическом пространстве называется .

Утверждение 2. Пусть множество  фиксировано; тогда функция , сопоставляющая каждой точке  расстояние , непрерывна на пространстве .

Доказательство. Воспользуемся определением непрерывности: функция  называется непрерывной в точке , если .

Из неравенства , где , получаем . Аналогично . Из полученных неравенств следует .

Для произвольного  возьмем . Тогда из неравенства  следует . Непрерывность  доказана.

Лемма. – замкнутое множество в метрическом пространстве . Для любого  расстояние от  до множества  положительно.

Доказательство.

Множество  замкнуто, отсюда следует, что множество - открыто. Так как точка  принадлежит открытому множеству , то существует такое, что . Так как , то  для некоторого . Поэтому для любого . Следовательно, , что и требовалось доказать.

Свойство 2. Метризуемое пространство нормально.

Доказательство. По доказанному метризуемое пространство является

-пространством. Остается доказать, что любые непустые непересекающиеся замкнутые множества  и  имеют непересекающиеся окрестности.

Так как  и множество  замкнуто по условию, то для любого  по лемме .

Обозначим  и  для произвольных  и .

Множества и  открыты как объединения открытых шаров в  и содержат соответственно множества  и .

Следовательно,  - окрестность множества ,  - окрестность множества .

Докажем, что .

Предположим, что , то есть . Тогда из условия  следует, что для некоторого . Отсюда .

Аналогично получаем  для некоторого . Для определенности пусть . Тогда .

Получаем , для некоторой точки , что невозможно в силу определения расстояния от точки до множества.

Следовательно . Таким образом,  является -пространством, а, значит, нормальным пространством. Теорема доказана.

Свойство 3. В метризуемом пространстве выполняется первая аксиома счетности.

Доказательство. Пусть - произвольное открытое множество, содержащее точку . Так как открытые шары образуют базу топологии метрического пространства, то  содержится в  вместе с некоторым открытым шаром, то есть  для некоторых  и . По утверждению 1 найдется такое , что .

Возьмем , для которого . Тогда . Таким образом открытые шары ,  образуют определяющую систему окрестностей точки . Очевидно, что множество этих окрестностей счетно. Что и требовалось доказать.

Определение. Множеством типа или просто  - множеством пространства  называется всякое множество , являющееся объединением счетного числа замкнутых (в ) множеств.

Определение. Множеством типа  или просто  - множеством пространства  называется всякое множество , являющееся пересечением счетного числа открытых (в ) множеств.

Очевидно, что множества типа  и  являются взаимно дополнительными друг для друга.

Определение. Нормальное пространство, в котором всякое замкнутое множество является множеством типа , называется совершенно нормальным.

Утверждение 3. Нормальное пространство является совершенно нормальным тогда и только тогда, когда всякое открытое множество, принадлежащее этому пространству, является множеством типа .

Свойство  4. Метризуемое пространство совершенно нормально.

Доказательство. Пусть  - непустое замкнутое множество в . Тогда  для непрерывной функции  (непрерывность ее установлена в утверждении 2). Обозначим , множества  открыты в  как прообразы открытых множеств при непрерывном отображении. Докажем, что .

Пусть , тогда . Так как  для любого , то  для любого . Отсюда .

Обратно. Пусть , тогда  для любого . Отсюда  для любого , поэтому  для любого , тогда , значит . Таким образом множество  является множеством типа .

Определение. Множество  всюду плотно в , если любое непустое открытое в  множество содержит точки из .

Определение. Топологическое пространство  называется сепарабельным, если оно имеет счетное всюду плотное подмножество.

Определение. Семейство γ открытых в  множеств образуют покрытие пространства , если  содержится в объединении множеств этого семейства.

Определение. Топологическое пространство  называется финально компактным, если из любого его открытого покрытия можно выделить счетное подпокрытие.

Свойство 5. Для метризуемого пространства  следующие условия эквивалентны:

1)  сепарабельно,

2)  имеет счетную базу,

3)  финально компактно.

Доказательство.

Пусть - счетное всюду плотное множество в , - метрика в . Множество окрестностей  счетно. Докажем, что  - база топологии в . Пусть - произвольное открытое в  множество, . Тогда  для некоторого . Рассмотрим рациональное число , для которого и точку , для которой .

Докажем, что . Пусть . Так как , то . Тогда . Таким образом, для произвольного  и открытого множества  нашелся элемент из , такой, что . Следовательно - база топологии.

 Пусть  - счетная база в . Рассмотрим произвольное открытое покрытие множества , - открыты для любого  (- индексное множество). Для любого  существует , для которого . Так как - база, то найдется такое , что . Тогда . Поскольку база  счетна, то  покрывается счетным числом соответствующих множеств . Таким образом, - финально компактно.

 Для каждой точки  рассмотрим окрестности , которые образуют покрытие пространства . В силу финальной компактности  из этого покрытия можно выделить счетное подпокрытие . В каждом из этих множеств выберем точку . Множество точек  счетно, докажем, что оно плотно в . Пусть - произвольное открытое множество в , , тогда  для некоторого . Существует элемент подпокрытия . Тогда , то есть любое непустое открытое множество в  содержит точку этого множества. Что и требовалось доказать.

Определение. Диаметром непустого множества  в метрическом пространстве  называется точная верхняя грань множества всех расстояний между точками множества  и обозначается .

.

Если , то множество  называют неограниченным.

Определение. Метрика  метрического пространства  называется ограниченной, если .

Свойство 6. Любое метризуемое топологическое пространство может быть метризовано ограниченной метрикой.

Доказательство. Пусть метрика  порождает топологию топологического пространства . Положим  для любых .

Докажем следующее:

1.   -метрика на ;

2.   метрики  и  эквивалентны;

3.   .