Навигация
Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путем расчетов
1.2. Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путем расчетов
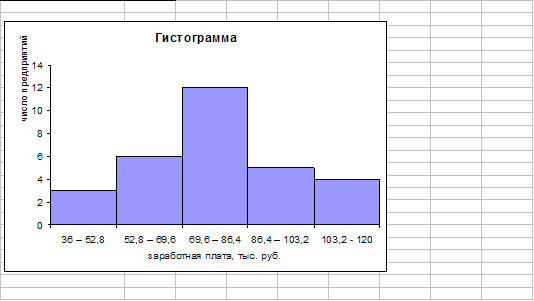
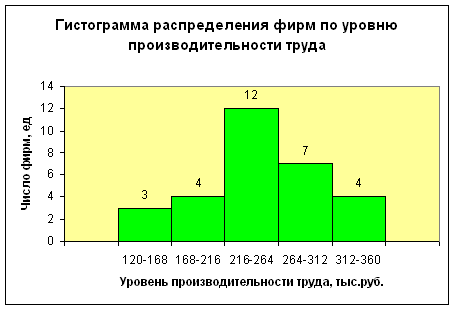
Мода Мо для дискретного ряда – это значение признака, наиболее часто встречающееся у единиц исследуемой совокупности[1]. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту). Более точно моду можно определить графическим методом по гистограмме ряда (рис.1).
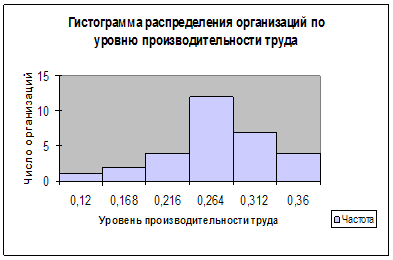
Конкретное значение моды для интервального ряда рассчитывается по формуле:
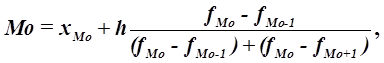 (3)
(3)
где хМo– нижняя граница модального интервала,
h –величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего модальному,
fMo+1– частота интервала, следующего за модальным.
Согласно табл.1.3 модальным интервалом построенного ряда является интервал 0,216 – 0,264 млн. руб., так как его частота максимальна (f3 = 12).
Расчет моды по формуле (3):
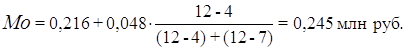
Вывод. Для рассматриваемой совокупности организаций наиболее распространенный уровень производительности труда характеризуется средней величиной 0,245 млн. руб.
Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности.
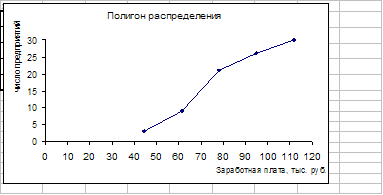
Медиану можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным частотам (табл. 5, графа 5).
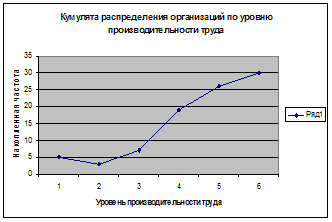
Конкретное значение медианы для интервального ряда рассчитывается по формуле: 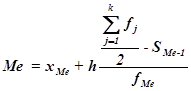 , (4)
, (4)
где хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
![]() – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.
Расчет значения медианы по формуле (4):

Вывод. В рассматриваемой совокупности организаций половина имеют в среднем уровень производительности труда не более 0,26 млн. руб., а другая половина – не менее 0,26 млн. руб.
3. Расчет характеристик ряда распределения
Для расчета характеристик ряда распределения ![]() , σ, σ2, Vσ строится таблица 6 (
, σ, σ2, Vσ строится таблица 6 (![]() – середина j-го интервала).
– середина j-го интервала).
Таблица 6
| Группы организаций по уровню производительности труда, млн руб. | Середина интервала,
| Число организаций, fj |
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0,12 – 0,168 | 0,144 | 3 | 0,432 | -0,104 | 0,011 | 0,033 |
| 0,168 – 0,216 | 0,192 | 4 | 0,768 | -0,056 | 0,003 | 0,012 |
| 0,216 – 0,264 | 0,24 | 12 | 2,88 | -0,008 | 0,00006 | 0,0007 |
| 0,264 – 0,312 | 0,288 | 7 | 2,016 | 0,04 | 0,002 | 0,014 |
| 0,312 – 0,36 | 0,336 | 4 | 1,344 | 0,088 | 0,008 | 0,032 |
| Итого | 30 | 7,44 | 0,092 |
Расчетная таблица для нахождения характеристик ряда распределения
Расчет средней арифметической взвешенной:
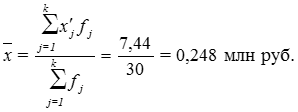 (5)
(5)
Расчет среднего квадратического отклонения:
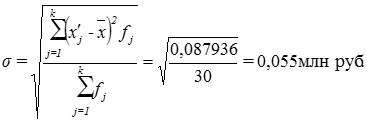 (6)
(6)
Расчет дисперсии:
σ2 =0,0552=0,003
Расчет коэффициента вариации:
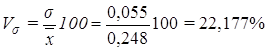 (7)
(7)
Вывод. Анализ полученных значений показателей ![]() и σ говорит о том, что средний уровень производительности труда составляет 0,248 млн. руб., отклонение от среднего уровня в ту или иную сторону составляет в среднем 0,054 млн. руб. (или 22,177%), наиболее характерные значения уровня производительности труда находятся в пределах от 0,194 млн. руб. до 0,302 млн. руб. (диапазон
и σ говорит о том, что средний уровень производительности труда составляет 0,248 млн. руб., отклонение от среднего уровня в ту или иную сторону составляет в среднем 0,054 млн. руб. (или 22,177%), наиболее характерные значения уровня производительности труда находятся в пределах от 0,194 млн. руб. до 0,302 млн. руб. (диапазон ![]() ).
).
Значение Vσ = 22,177% не превышает 33%, следовательно, вариация уровня производительности в исследуемой совокупности незначительна и совокупность по данному признаку качественно однородна. Расхождение между значениями ![]() , Мо и Ме незначительно (
, Мо и Ме незначительно (![]() =0,248млн руб., Мо=0,24млн руб., Ме=0,26млн руб.), что подтверждает вывод об однородности совокупности. Таким образом, найденное среднее значение уровня производительности труда (0,248 млн руб.) является типичной, надежной характеристикой исследуемой совокупности организаций.
=0,248млн руб., Мо=0,24млн руб., Ме=0,26млн руб.), что подтверждает вывод об однородности совокупности. Таким образом, найденное среднее значение уровня производительности труда (0,248 млн руб.) является типичной, надежной характеристикой исследуемой совокупности организаций.
4.Вычисление средней арифметической по исходным данным
Для расчета применяется формула средней арифметической простой:
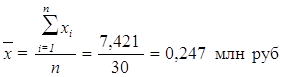 , (8)
, (8)
Причина расхождения средних величин, рассчитанных по формулам (8) и (5), заключается в том, что по формуле (8) средняя определяется по фактическим значениям исследуемого
признака для всех 30-ти банков, а по формуле (5) средняя вычисляется для интервального ряда, когда в качестве значений признака берутся середины интервалов ![]() и, следовательно, значение средней будет менее точным (за исключением случая равномерного распределения значений признака внутри каждой группы).
и, следовательно, значение средней будет менее точным (за исключением случая равномерного распределения значений признака внутри каждой группы).
2.2.Задание 2
По исходным данным (табл. 1) с использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1. Установить наличие и характер корреляционной связи между признаками Уровень производительности труда и Фондоотдача, образовав по каждому признаку четыре группы с равными интервалами, используя методы:
а) аналитической группировки;
б) корреляционной таблицы.
Похожие работы
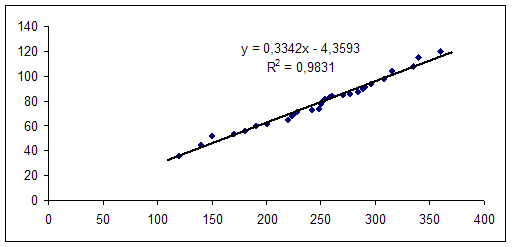
... на зависимую и определение расчётных значений зависимой переменной (функции регрессии). Решение всех названных задач приводит к необходимости комплексного использования этих методов. Корреляционный и регрессионный анализ. Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле ...
... колеблется в пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем больше влияние оказывает факторный признак на результативный. Для изучения взаимосвязи между производительностью труда и заработной платой проведем дисперсионный анализ на основе результатов проведенной аналитической группировки (смотри таблицу 1) Средний уровень производительности труда по 30 предприятиям составляет ...
... . В то же время в рассматриваемой ситуации снижение удельного веса дебиторской задолженности отмечает положительную тенденцию. [5, c.240-242] 1.2. Бухгалтерский учет в системе управления предприятием В бухгалтерии предприятия - в этом центральном звене внутреннего производственного учета и отчетности аккумулируются все фактические издержки и распределяются по местам их возникновения (цехам, ...
... между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной. Решение названных задач опирается на соответствующие приемы, ...
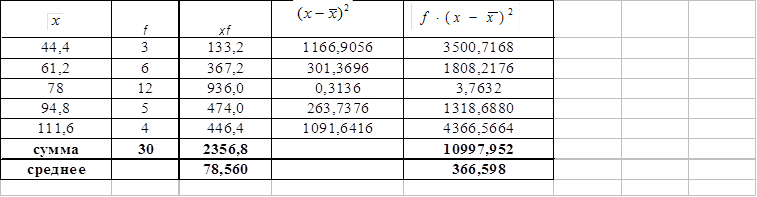
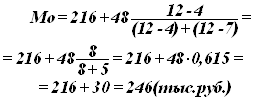
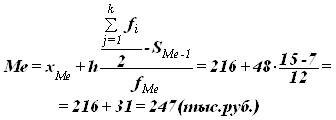
0 комментариев