Навигация
Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения
2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения
Эмпирический коэффициент детерминации ![]() оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель
оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель ![]() рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
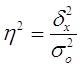 , (9)
, (9)
где ![]() – общая дисперсия признака Y,
– общая дисперсия признака Y,![]()
![]() – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Значения показателя ![]() изменяются в пределах
изменяются в пределах ![]() . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство
. При отсутствии корреляционной связи между признаками Х и Y имеет место равенство ![]() =0, а при наличии функциональной связи между ними - равенство
=0, а при наличии функциональной связи между ними - равенство![]() =1.
=1.
Общая дисперсия ![]() характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
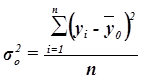 ,
(10)
,
(10)
где yi – индивидуальные значения результативного признака;
![]() – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Общая средняя ![]() вычисляется как средняя арифметическая простая по всем единицам совокупности:
вычисляется как средняя арифметическая простая по всем единицам совокупности:
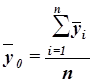 (11)
(11)
или как средняя взвешенная по частоте групп интервального ряда:
 (12)
(12)
Для вычисления ![]() удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.
удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.
Расчет ![]() по формуле (11):
по формуле (11):
![]()
Для расчета общей дисперсии ![]() применяется вспомогательная таблица 12.
применяется вспомогательная таблица 12.
Таблица 12
Вспомогательная таблица для расчета общей дисперсии
| Номер организации п/п | Фондоотдача, млн руб. |
|
|
|
| 1 | 2 | 3 | 4 | 5 |
| 1 | 1,05 | -0,044 | 0,002 | 1,102 |
| 2 | 0,96 | -0,134 | 0,018 | 0,922 |
| 3 | 1,12 | 0,026 | 0,0006 | 1,254 |
| 4 | 1,19 | 0,096 | 0,009 | 1,416 |
| 5 | 1,08 | -0,014 | 0,0002 | 1,166 |
| 6 | 0,98 | -0,114 | 0,013 | 0,96 |
| 7 | 1,3 | 0,206 | 0,042 | 1,69 |
| 8 | 1,16 | 0,066 | 0,004 | 1,346 |
| 9 | 1,065 | -0,029 | 0,0008 | 1,134 |
| 10 | 1 | -0,094 | 0,009 | 1 |
| 11 | 1,1 | 0,006 | 0,00004 | 1,21 |
| 12 | 1,23 | 0,136 | 0,018 | 1,513 |
| 13 | 1,13 | 0,036 | 0,001 | 1,277 |
| 14 | 1,03 | -0,064 | 0,004 | 1,06 |
| 15 | 0,9 | -0,194 | 0,037 | 0,81 |
| 16 | 1,06 | -0,034 | 0,001 | 1,124 |
Продолжение таблицы 12
| 17 | 1,15 | 0,056 | 0,003 | 1,322 |
| 18 | 1,07 | -0,024 | 0,0006 | 1,145 |
| 19 | 1,17 | 0,076 | 0,006 | 1,369 |
| 20 | 0,94 | -0,154 | 0,024 | 0,883 |
| 21 | 1,02 | -0,074 | 0,005 | 1,04 |
| 22 | 1,06 | -0,034 | 0,001 | 1,124 |
| 23 | 1,18 | 0,086 | 0,007 | 1,392 |
| 24 | 0,99 | -0,104 | 0,011 | 0,98 |
| 25 | 1,1 | 0,006 | 0,00004 | 1,21 |
| 26 | 1,28 | 0,186 | 0,035 | 1,638 |
| 27 | 1,09 | -0,004 | 0,00001 | 1,188 |
| 28 | 1,25 | 0,156 | 0,024 | 1,562 |
| 29 | 1,04 | -0,054 | 0,003 | 1,082 |
| 30 | 1,12 | 0,026 | 0,0007 | 1,254 |
| Итого | 32,815 | 0,005 | 0,283 | 36,177 |
Расчет общей дисперсии по формуле (10):
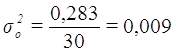
Общая дисперсия может быть также рассчитана по формуле
![]() ,
,
где ![]() – средняя из квадратов значений результативного признака,
– средняя из квадратов значений результативного признака,
![]() – квадрат средней величины значений результативного признака.
– квадрат средней величины значений результативного признака.

![]()
Тогда
![]()
Межгрупповая дисперсия ![]() вычисляется по формуле:
вычисляется по формуле:
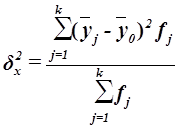 , (13)
, (13)
где ![]() –групповые средние,
–групповые средние,
![]() – общая средняя,
– общая средняя,
![]() –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета
межгрупповой дисперсии ![]() строится
вспомогательная таблица 13.
строится
вспомогательная таблица 13.
Таблица 13
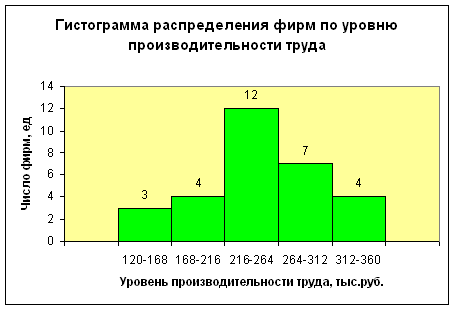
Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы организаций по уровню производительности труда, млн. руб. | Число организаций,
| Среднее значение |
|
|
| 1 | 2 | 3 | 4 | 5 |
| 0,12 – 0,168 | 3 | 0,933 | -0,16 | 0,077 |
| 0,168 – 0,216 | 4 | 0,997 | -0,096 | 0,037 |
| 0,216 – 0,264 | 12 | 1,072 | -0,022 | 0,006 |
| 0,264 – 0,312 | 7 | 1,157 | 0,063 | 0,028 |
| 0,312 – 0,36 | 4 | 1,265 | 0,171 | 0,117 |
| Итого | 30 | 0,265 |
Расчет межгрупповой дисперсии ![]() по формуле (11):
по формуле (11):
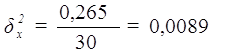
Расчет эмпирического коэффициента детерминации ![]() по формуле (9):
по формуле (9):
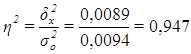 или 94,7%
или 94,7%
Вывод. 94,68% вариации фондоотдачи организаций обусловлено вариацией уровня производительности труда, а 5,3% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение ![]() оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле:
оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле:
 (14)
(14)
Значение показателя изменяются в пределах ![]() . Чем ближе значение
. Чем ближе значение ![]() к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе
к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе ![]() служит шкала Чэддока (табл. 14):
служит шкала Чэддока (табл. 14):
Таблица 14
Шкала Чэддока
| h | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика силы связи | Слабая | Умеренная | Заметная | Тесная | Весьма тесная |
Расчет эмпирического корреляционного отношения ![]() по формуле (14):
по формуле (14):
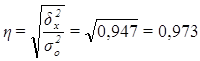 или 97,3%
или 97,3%
Вывод. Согласно шкале Чэддока связь между уровнем производительности труда и фондоотдачей организаций является весьма тесной.
2.3.Задание 3
По результатам выполнения Задания 1 с вероятностью 0,683 необходимо определить:
1) ошибку выборки среднего уровня производительности труда и границы, в которых будет находится средний уровень производительности труда в генеральной совокупности.
2) ошибку выборки доли организаций с уровнем производительности труда 264 тыс. руб. и более, а также границы, в которых будет находиться генеральная доля.
Выполнение Задания 3
Целью выполнения данного Задания является определение для генеральной совокупности коммерческих организаций границ, в которых будут находиться величина среднего уровня производительности труда и доля организаций с уровнем производительности труда не менее 264 тыс. руб.
Похожие работы
... на зависимую и определение расчётных значений зависимой переменной (функции регрессии). Решение всех названных задач приводит к необходимости комплексного использования этих методов. Корреляционный и регрессионный анализ. Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле ...
... колеблется в пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем больше влияние оказывает факторный признак на результативный. Для изучения взаимосвязи между производительностью труда и заработной платой проведем дисперсионный анализ на основе результатов проведенной аналитической группировки (смотри таблицу 1) Средний уровень производительности труда по 30 предприятиям составляет ...
... . В то же время в рассматриваемой ситуации снижение удельного веса дебиторской задолженности отмечает положительную тенденцию. [5, c.240-242] 1.2. Бухгалтерский учет в системе управления предприятием В бухгалтерии предприятия - в этом центральном звене внутреннего производственного учета и отчетности аккумулируются все фактические издержки и распределяются по местам их возникновения (цехам, ...
... между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной. Решение названных задач опирается на соответствующие приемы, ...
0 комментариев