Навигация
Вычисление средней арифметической по исходным данным о среднегодовой заработной плате
4. Вычисление средней арифметической по исходным данным о среднегодовой заработной плате
Для расчета применяется формула средней арифметической простой:
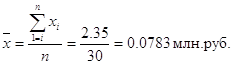 ,
,
Причина расхождения средних величин, рассчитанных по исходным данным (0.0783 млн.руб.) и по интервальному ряду распределения (0.079 млн.руб.), заключается в том, что в первом случае средняя определяется по фактическим значениям исследуемого признака для всех 30-ти предприятий, а во втором случае в качестве значений признака берутся середины интервалов ![]() и, следовательно, значение средней будет менее точным. Вместе с тем, при округлении обеих рассматриваемых величин их значения совпадают (0.079 млн.руб.), что говорит о достаточно равномерном распределении среднегодовой заработной платы внутри каждой группы интервального ряда.
и, следовательно, значение средней будет менее точным. Вместе с тем, при округлении обеих рассматриваемых величин их значения совпадают (0.079 млн.руб.), что говорит о достаточно равномерном распределении среднегодовой заработной платы внутри каждой группы интервального ряда.
Задание 2
По исходным данным (табл. 1) с использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1. Установить наличие и характер корреляционной связи между признаками Уровень производительности труда и Среднегодовая заработная плата, образовав пять групп с равными интервалами по каждому из признаков, используя методы:
а) аналитической группировки; б) корреляционной таблицы.
2. Измерить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения задания 2.
Выполнение задания 2
Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, а также установление направления связи и оценка ее тесноты.
По условию Задания 2 факторным является признак Уровень производительности труда, результативным – признак Среднегодовая заработная плата.
1. Установление наличия и характера корреляционной связи между признаками Уровень производительности труда и Среднегодовая заработная плата методами аналитической группировки и корреляционных таблиц
1а. Применение метода аналитической группировки
Аналитическая группировка строится по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение ![]() результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения ![]() систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х- Уровень производительности труда и результативным признаком Y – Среднегодовая заработная Групповые средние значения ![]() получаем из таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 8:
получаем из таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 8:
Таблица 8 Зависимость среднегодовой заработной платы от уровня производительности труда
| Номер группы | Группы предприятий по уровню производительности труда, млн.руб., x | Число предприятий, fj | Среднегодовая заработная плата, млн.руб. | |
| всего | в среднем на одно предприятие, | |||
| 1 | 2 | 3 | 4 | 5=4:3 |
| 1 | 0.12-0.168 | 3 | 0.133 | 0,044 |
| 2 | 0.168-0.216 | 4 | 0.232 | 0,058 |
| 3 | 0.216-0.264 | 12 | 0.907 | 0,076 |
| 4 | 0.264-0.312 | 7 | 0.631 | 0,090 |
| 5 | 0.312-0.36 | 4 | 0.447 | 0,112 |
|
| ИТОГО | 30 | 2.35 | 0,38 |
Вывод. Анализ данных табл. 8 показывает, что с увеличением уровня производительности труда от группы к группе систематически возрастает и среднегодовая заработная плата по каждой группе предприятий, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.
1б. Применение метода корреляционных таблиц
Корреляционная таблица строится как комбинация двух рядов распределения по факторному признаку Х и результативному признаку Y. На пересечении j-ой строки и k-ой графы таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый интервал по признаку Y. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками - прямой или обратной. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему, обратная - по диагонали от правого верхнего угла к левому нижнему.
Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Для факторного признака Х – Уровень производительности труда построим таблицу:
Таблица 8.1
| № предприятия п/п | уровень производительности труда, млн. руб. | № предприятия п/п | уровень производительности труда, млн. руб. |
|
|
| ||
| 1 | 0,225 | 16 | 0,228 |
| 2 | 0,15 | 17 | 0,284 |
| 3 | 0,26 | 18 | 0,25 |
| 4 | 0,308 | 19 | 0,29 |
| 5 | 0,251 | 20 | 0,14 |
| 6 | 0,17 | 21 | 0,2 |
| 7 | 0,36 | 22 | 0,242 |
| 8 | 0,288 | 23 | 0,296 |
| 9 | 0,248 | 24 | 0,18 |
| 10 | 0,19 | 25 | 0,258 |
| 11 | 0,254 | 26 | 0,34 |
| 12 | 0,315 | 27 | 0,252 |
| 13 | 0,276 | 28 | 0,335 |
| 14 | 0,22 | 29 | 0,223 |
| 15 | 0,12 | 30 | 0,27 |
Определяем величину интервала для результативного признака Y – Среднегодовая заработная плата при k = 5, уmax = 0.12 млн руб., уmin = 0.036 млн .руб.:
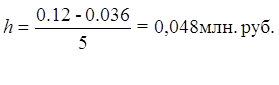
Границы интервалов ряда распределения результативного признака Y имеют вид:
Таблица 9
| Номер группы | Нижняя граница, млн руб. | Верхняя граница, млн руб. |
| 1 | 0.12 | 0.168 |
| 2 | 0.168 | 0.216 |
| 3 | 0.216 | 0.264 |
| 4 | 0.264 | 0.312 |
| 5 | 0.312 | 0.36 |
Подсчитывая для каждой группы число входящих в нее предприятий с использованием принципа полуоткрытого интервала [ ), получаем интервальный ряд распределения результативного признака (табл. 10).
Таблица 10 Интервальный ряд распределения предприятий по признаку среднегодовая заработная плата
| Группы предприятий по признаку среднегодовая заработная плата, млн руб., у | Число предприятий, fj |
| 0.12-0.168 | 3 |
| 0.168-0.216 | 4 |
| 0.216-0.264 | 12 |
| 0.264-0.312 | 7 |
| 0.312-0.36 | 4 |
| ИТОГО | 30 |
Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 11).
Таблица 11 Корреляционная таблица зависимости среднегодовой заработной платы от уровня производительности труда
| Группы предприятий по признаку среднегодовая заработная плата, млн.руб. | Группы предприятий по признаку уровень производительности труда, млн. руб. | ИТОГО | |||||
| 0.036-0.0528 | 0.0528-0.0696 | 0.0696-0.0864 | 0.0864-0.1032 | 0.1032-0.12 | |||
| 0.12-0.168 | 3 | 3 | |||||
| 0.168-0.216 | 4 | 4 | |||||
| 0.216-0.264 | 2 | 10 | 12 | ||||
| 0.264-0.312 | 2 | 5 | 7 | ||||
| 0.312-0.36 | 4 | 4 | |||||
| ИТОГО | 3 | 6 | 12 | 5 | 4 | 30 | |
Вывод. Анализ данных табл. 11 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между уровнем производительности труда и среднегодовой заработной платой.
2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации ![]() и эмпирического корреляционного отношения
и эмпирического корреляционного отношения ![]()
Коэффициент детерминации ![]() характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии
характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии ![]() признака Y в его общей дисперсии
признака Y в его общей дисперсии![]() :
:
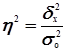
где ![]() – общая дисперсия признака Y,
– общая дисперсия признака Y,
![]() – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Общая дисперсия ![]() характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных) и вычисляется по формуле
характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных) и вычисляется по формуле
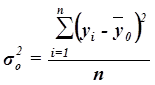 , (10)
, (10)
где yi – индивидуальные значения результативного признака;
![]() – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Межгрупповая дисперсия ![]() измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка) и вычисляется по формуле
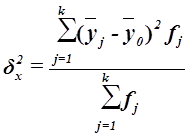 , (13)
, (13)
где ![]() –групповые средние,
–групповые средние,
![]() – общая средняя,
– общая средняя,
![]() –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета показателей ![]() и
и ![]() необходимо знать величину общей средней
необходимо знать величину общей средней ![]() , которая вычисляется как средняя арифметическая простая по всем единицам совокупности:
, которая вычисляется как средняя арифметическая простая по всем единицам совокупности:
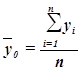
Значения числителя и знаменателя формулы имеются в табл. 8 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую среднюю ![]() :
:
![]() =
= ![]() =0.078 млн руб.
=0.078 млн руб.
Для расчета общей дисперсии ![]() применяется вспомогательная таблица 12.
применяется вспомогательная таблица 12.
Таблица 12 Вспомогательная таблица для расчета общей дисперсии
| № предприятия | Среднегодовая заработная плата, млн. руб. |
|
|
| 1 | 2 | 3 | 4 |
| 1 | 0.07 | 0,019 | 0,0004 |
| 2 | 0.052 | 0,481 | 0,2310 |
| 3 | 0.084 | 0,781 | 0,6094 |
| 4 | 0.098 | 0,681 | 0,4633 |
| 5 | 0.079 | 0,281 | 0,0788 |
| 6 | 0.054 | 0,181 | 0,0326 |
| 7 | 0.12 | 0,381 | 0,1449 |
| 8 | 0.09 | 0,119 | 0,0142 |
| 9 | 0.074 | 0,319 | 0,1020 |
| 10 | 0.06 | 0,381 | 0,1449 |
| 11 | 0.082 | 0,019 | 0,0004 |
| 12 | 0.104 | 0,681 | 0,4633 |
| 13 | 0.086 | 0,481 | 0,2310 |
| 14 | 0.065 | 0,069 | 0,0048 |
| 15 | 0.036 | 0,181 | 0,0326 |
| 16 | 0.071 | 0,719 | 0,5174 |
| 17 | 0.087 | 0,281 | 0,0788 |
| 18 | 0.078 | 0,019 | 0,0004 |
| 19 | 0.091 | 0,219 | 0,0481 |
| 20 | 0.045 | 0,281 | 0,0788 |
| 21 | 0.062 | 0,069 | 0,0048 |
| 22 | 0.073 | 0,169 | 0,0287 |
| 23 | 0.094 | 0,189 | 0,0358 |
| 24 | 0.056 | 0,219 | 0,0481 |
| 25 | 0.083 | 0,319 | 0,1020 |
| 26 | 0.115 | 0,419 | 0,1758 |
| 27 | 0.08 | 0,319 | 0,1020 |
| 28 | 0.108 | 0,719 | 0,5174 |
| 29 | 0.068 | 0,619 | 0,3836 |
| 30 | 0.085 | 0,519 | 0,2697 |
| Итого | 0.0107 |
Рассчитаем общую дисперсию:
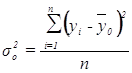 =
=![]()
Для расчета межгрупповой дисперсии ![]() строится вспомогательная таблица 13. При этом используются групповые средние значения
строится вспомогательная таблица 13. При этом используются групповые средние значения ![]() из табл. 8 (графа 5).
из табл. 8 (графа 5).
| Группы предприятий по признаку среднегодовая заработная плата, млн.руб., x | Число предприятий, fj | Среднее значение в группе, млн руб.
|
|
|
| 1 | 2 | 3 | 4 | 5 |
| 0.12-0.168 | 3 | 0.04 | 0.0014 | 1.0042 |
| 0.168-0.216 | 4 | 0.058 | 0.0014 | 1.0016 |
| 0.216-0.264 | 12 | 0.075 | 0.0000 | 0.0001 |
| 0.264-0.312 | 7 | 0.09 | 0.0001 | 0.001 |
| 0.312-0.36 | 4 | 0.11 | 0.001 | 0.004 |
| ИТОГО | 30 | 0.0119 |
Рассчитаем межгрупповую дисперсию:
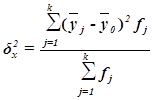
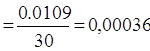
![]() =
= ![]() -
- ![]() ²= 0,0064 – 0,078²= 0,0064 – 0,006 = 0,0004
²= 0,0064 – 0,078²= 0,0064 – 0,006 = 0,0004
Определяем коэффициент детерминации:
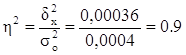
η= ![]() =
= ![]() = 0,95
= 0,95
Вывод. 90% вариации среднегодовой заработной платы предприятий обусловлено вариацией уровня производительности труда.
Связь между признаками весьма высокая, о чем говорит η=0,95 и близкое к 1.
Задание 3
По результатам выполнения Задания 1 с вероятностью 0,954 необходимо определить:
1) ошибку выборки для средней величины среднегодовой заработной платы, а также границы, в которых будет находиться генеральная средняя.
2) Ошибку выборки доли предприятий с уровнем среднегодовой заработной платы 86.4 тыс.руб. и более и границы, в которых будет находиться генеральная доля.
Выполнение Задания 3
Целью выполнения данного Задания является определение для генеральной совокупности предприятий региона границ, в которых будет находиться средняя величина среднегодовой заработной платы.
Похожие работы
... труда. Получая высокую заработную плату, рабочие хорошо питаются, увеличивая свои физические силы, а надежда улучшить свое положение побуждает их к производительной работе. 2. АНАЛИЗ ТРУДА И ЗАРАБОТНОЙ ПЛАТЫ В ЗАО «РММ» 2.1 Финансовый анализ предприятия Закрытое акционерное общество "РММ" образовано на основе решения Общего собрания акционеров (Протокол N ...
... выданных раздатчикам денег на выдачу заработной платы. Однако такая книга в бухгалтерии предприятия не ведется, что тоже следует отметить как недостаток организации бухгалтерского учета труда и заработной платы в организации. Заработную плату выдают в течение трех дней. По истечении этого срока раздатчики против фамилий работников, не получивших заработную плату, делает отметку «депонировано» и ...
... с экономической точки зрения, здесь непременно выходят на свет смежные с экономикой дисциплины, о которых уже упоминалось во введении к данной работе. В самом деле, не может быть однозначных ответов по вопросам заработной платы и доходов в России. Это то же самое, как если бы некто заявил, что знает ответы на два извечных русских вопроса: «Кто виноват?» и «Что делать?». Также при изучении данной ...
... 137 дней. По результатам проведенной оценки финансового состояния можно сделать вывод, что перед предприятием стоит проблема выживания. Глава 3. Исследование путей повышения производительности труда 3.1 Резервы и факторы роста производительности труда на предприятии При анализе и планировании производительности труда важнейшей задачей является выявление и использование резервов ее роста ...


0 комментариев