Утвердить период начисления, выплат и использования средств, направленных на выплаты дотаций сельскохозяйственным производителям
Экономико-статистический анализ доходности производства молока
Определение формы и параметров уравнения связи;
Индексный анализ изменения валового выхода молока в ЗАСТ «Батькивщина» в 2009 г. по сравнению с 2006 г
Анализ показателей рентабельности производства молока в ЗАСТ «Батькивщина»
Анализ себестоимости производства молока и факторов, влияющих на ее изменения в ЗАСТ «Батькивщина» в сравнении за два года
Анализ эффективности использования кормов при производстве молока в ЗАСТ «Батькивщина» в 2009 г. по сравнению с 2008 г
Пути повышения доходности производства молока в ЗАСТ «Батькивщина»
Навигация
Экономико-статистический анализ доходности производства молока
Экономико-статистический анализ и выявление резервов доходности производства молока в ЗАСТ "Батькивщина" п. Бирюково Луганской области
54560
знаков
19
таблиц
0
изображений
3. Экономико-статистический анализ доходности производства молока
3.1 Группировка хозяйств Троицкого района Луганской области по влиянию цены реализации 1 ц молока на изменение уровня окупаемости затрат
Предмет статистических исследований – массовые общественные явления – обладают многочисленными признаками и свойствами. Обобщить статистические данные, раскрыть наиболее существенные особенности, формы движения массового явления в целом и отдельно составляющих невозможно без определенно полученных принципов обработки данных.
Группировка – исходный и необходимый прием, предшествующий исчислению многих статистических характеристик; неправильное ее применение влечет за собой свертывание статистического анализа, превращение показателей сводки в цифры, лишенные смысла и значения. Статистические группировки – один важный этап статистической сводки, позволяющий выделить из массы первичного статистического материала, представляют собой ряды цифр, однородные группы единиц, обладающие общим сходством в качественном и количественном отношениях. Группировка – это не просто один из методов, который можно использовать при статистическом анализе.
Таким образом, группировка – расчленение общей совокупности единиц по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в качественном и количественном отношении и позволяющие выделить социально-экономические типы, изучить структуру совокупности или проанализировать связи между отдельными признаками.
Таблица 6. Группировка хозяйств Троицкого района Луганской области по влиянию средней цены реализации 1 ц молока на изменение уровня окупаемости затрат
| Название хозяйства | Цена реализации 1 ц., грн. | Окупаемость затрат, % |
| 1. «Авангард» 2. «Аграрник» 3. «Араповское» 4. «Артемида» 5. «Батькивщина» 6. «Воеводское» 7. Врубовщик 8. «Дружба» 9. «Злагода» 10. «Лан» 11. «Малоалександровка» 12. «Новознаменское» 13. «Покровское» 14. «Правда» 15. «Приволье» 16. «Проминь» 17. «Распасивка» 18. «Рубин» 19. «Слобожанское» 20. «Тарасивское» 21. «Тополи» 22. «Угольщик» | 60,9 43 58 57 61 49,8 46 55 60,2 46 56,2 50 56 50,2 55,8 51 56,4 53,2 51,2 43,7 51,5 60 | 52,7 20,6 62 122 107 77 65 28 53 68 42 82 46 56 45 20 49 97 52 90 60 103 |
Теперь нам необходимо построить ранжированный ряд распределения хозяйств по цене реализации 1 ц молока в порядке возрастания признака.
Таблица 7. Ранжированный ряд
| Название хозяйства | Цена реализации 1 ц., грн. | Окупаемость затрат, % |
| |
| 1. «Аграрник» 2. «Тарасовское» 3. «Врубовщик» 4. «Лан» 5. «Воеводское» 6. «Новознаменское» 7. «Правда» 8. «Промінь» 9. «Слобожанское» 10. «Тополи» 11. «Рубин» 12. «Дружба» 13. «Приволье» 14. «Покровское» 15. «Малоалександровка» 16. «Распасеевка» 17. «Артемида» 18. «Араповское» 19. «Угольщик» 20. Злагода» 21. «Авангард» 22. «Батькивщина» | 43 43,7 46 46 49,8 50 50,2 51 51,2 52,1 53,2 55 55,8 56 56,2 56,4 57,0 58 60 60,2 60,9 61 | 20,6 19,0 65 68 77 82 56 19,8 52 60 97 28 45 46 42 99,2 122 62 103 53 52,7 107 | ||
При построении ряда распределения возникает вопрос о количестве интервалов и их величине. В данном случае для определения количества интервалов мы можем воспользоваться формулой Стерджесса:
n=1+3.322*lg N, где
N – число единиц совокупности
n = 5
Теперь определим границы (ширину) интервалов по формуле:
;
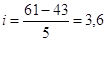
Существует нижняя и верхняя границы интервалов. Нижняя граница первого интервала (х mіn). Если к х min добавить величину интервала (i) – получим верхнюю границу первого интервала. Верхняя граница 1 интервала служит одновременно нижней границей 2 интервала и т.д.
1 интервал 43… 46,6
2 интервал 46,6… 50,2
3 интервал 50,2… 53,8
4 интервал 53,8… 57,4
5 интервал 57,4…. 61
Таблица 8. Интервальный вариационный ряд распределения 21 хозяйств по цене реализации 1 ц молока.
| Номер группы | Границы интервалов по цене реализации | Число хозяйств |
| 1 | 43–46,6 | 4 |
| 2 | 46,6–50,2 | 3 |
| 3 | 50,2–53,8 | 4 |
| 4 | 53,8–57,4 | 6 |
| 5 | 57,4 – 61 | 5 |
Важной характеристикой вариационного ряда распределения по району является средняя величина. Статистическая средняя величина показывает общий уровень вариационного признака и характеризует типический размер признака качественно-однородной совокупности в конкретных условиях места и времени.
Таблица 9. Зависимость уровня окупаемости затрат от цены реализации 1 ц молока в хозяйствах Троицкого района
| Номер группы | Границы интервалов по цене реализации 1 ц молока | Средняя цена реализации 1 ц молока | Средняя окупаемость затрат, грн. |
| 1 | 43–46,6 | 44,7 | 43,15 |
| 2 | 46,6–50,2 | 50 | 71,7 |
| 3 | 50,2–53,8 | 51,9 | 57,2 |
| 4 | 53,8–57,4 | 56,1 | 63,7 |
| 5 | 57,4 – 61 | 60,02 | 75,54 |
Из проведенного нами анализа видно, что влияние средняя цена реализации по району имеет прямое влияние на окупаемость затрат. При росте средней цены реализации 1 ц молока окупаемость затрат также возрастает. Соответственно, чем больше средняя цена реализации, тем выше средняя окупаемость затрат. Самая высокая окупаемость затрат в 5 группе 75,54 грн, на эту же группу приходится и самая высокая цена реализации 1 ц молока 60,02 грн.
Благодаря данной группировке, мы нашли передовое хозяйство, им является СООО «Авангард», так как в этом хозяйстве средняя цена 1 ц молока при реализации самая высокая 61 грн, это касается и окупаемости затрат, она составляет 107 грн. В анализируемом хозяйстве ЗАСТ «Батькивщина» цена реализации составляет 60,9 грн., а окупаемость =52,7 грн.
3.2 Корреляционно-регрессионный анализ изменение уровня окупаемости затрат молока в хозяйствах Троицкого района Луганской области под влиянием цены реализации 1 центнера
Изучение реальной действительности показывает, что практически каждое общественное явление находится в тесной связи и взаимодействии с другими явлениями, какими бы случайными они не казались на первый взгляд. Например, уровень урожайности сельскохозяйственных культур зависит от множества природных и экономических факторов, тесно связанных между собой.
Исследуя связи между признаками, необходимо выделить, прежде всего, два вида связей: 1) функциональная и 2) корреляционная (статистическая) связь.
Функциональной называют тесную связь между признаками, при которой каждому значению одной переменной соответствует строго определенное значение другой переменной.
Но в социально-экономических явлениях функциональные связи встречаются редко. Здесь чаще наблюдаются такие связи между переменными величинами, при которых числовому значению одной из них отвечает несколько значений других. Такая связь называется корреляционной.
Примером корреляционной связи в сельскохозяйственном производстве может выступать изменение уровня окупаемости затрат под влиянием цены реализации 1 ц молока и продуктивности 1 головы.
С помощью корреляционного анализа решают два основных задания:
0 комментариев