Навигация
Математические основы
2. Математические основы
Математическими основами индуктивного и дедуктивного вывода являются математическая логика и ее развитие логика предикатов первого порядка.
Логика используется для того, чтобы доказывать правильность или неправильность тех или иных утверждений или высказываний. Это имеет большое значение при решении задач проектирования и для других вычислительных задач. Так искусственный интеллект во многом опирается на гипотезу символьных систем. Упрощенно эта гипотеза утверждает, что, организовав огромную структуру взаимосвязанных символов, представляющих реальные знания и сложный набор символьных процессов, позволяющий оперировать структурами с целью создания новых структур, можно создать машину, работающую также хорошо в смысле интеллектуальной деятельности, как человек.
2.1 Алгебра высказываний
Одним из основных понятий логики является понятие высказывания, правильность или неправильность которого мы стараемся определить. Попытаемся определить смысл этого термина. Высказыванием называют предложения, про которые разумно говорить, разумно считать, что они являются истинными или ложными. Неуточненность понятий «истинно» и «ложно» делают понятие высказывания расплывчатым. Однако, вводя ограничения можно это понятие уточнить. Фразы «Пойдем в кино?», «Да здравствует президент!» не являются высказываниями (как и любые вопросительные и восклицательные предложения). Фраза «Треугольник называется равносторонним, если все его стороны равны» (как и любое другое определение) также не является высказыванием. Фразы «2*2 = 4» и «3>5» - высказывания (первое истинное, второе ложное). Фраза «В повести “Шинель” 200755 букв» - высказывание, но нам неизвестна его истинность. Фразу «Эта книга хорошая» не следует относить к высказываниям в традиционной логике в силу неопределенности понятия «хороший».
Поэтому, определим, как простое высказывание – высказывание, для которого в определенных условиях времени и места можно делать вывод об его истинности или ложности, причем это высказывание задается простым предложением («Сегодня идет дождь»).
Из простых высказываний с помощью связок можно строить сложные высказывания, и тогда возникает задача определения их истинности в зависимости от истинности простых высказываний, его составляющих.
Переменную, в область значений которой входят только высказывания (а точнее истинностные значения T, F) будем называть высказывательной переменной (двоичной или булевой). В силу определения областью значений этих переменных является двоичный алфавит.
Функции от любого конечного числа двоичных переменных, также способные принимать лишь два значения T и F,принято называть булевыми функциями. Иногда такие функции называют переключательными, так как реализующие такие функции схемы осуществляют переключение входных каналов, подавая на них сигналы, то одного, то другого вида.
Областью определения булевых функций от n – переменных служит совокупность всевозможных n – мерных упорядоченных наборов (векторов размерностью n), компонентами которых являются буквы двоичного алфавита T и F.
Для любого n = 1, 2, . . . среди n – мерных наборов можно ввести естественную лексикографическую упорядоченность. Для этого поставим в соответствие с F – 0, а с T – 1. Тогда набор преобразуется в последовательность 0 и 1. Такой набор уже можно рассматривать как представление целого неотрицательного числа в двоичной системе счисления. Например, TTTF ® 1110 ® 14. Это число будем называть номером набора. Эти наборы называются также кортежами или, используя геометрическую терминологию, точками.
Последнее название связано с тем, что имеется естественная возможность отождествлять различные n – мерные наборы с вершинами n-мерного куба.
Естественную упорядоченность наборов мы получим, если расположим их в порядке возрастания номеров. Первым в таком расположении является нулевой набор, все компоненты которого 0, последним – набор, все компоненты которого 1.
Отсюда, наборы размерности n нумеруются числами от 0 до 2n-1. А отсюда в частности вытекает:
1. Имеется в точности 2n двоичных n-мерных наборов.
Нетрудно также подсчитать число различных булевых функций от n переменных. Для каждого набора значений, независимо от значений других наборов, можно выбрать в качестве значений функции T или F. Следовательно, прибавление каждого нового набора к области определения булевой функции увеличивает число различных булевых функций ровно в два раза.
На одном наборе можно определить две различных булевых функции. На двух – 22 и т. д. Продолжая подобным образом и с учетом 1, получим:
2. Имеется точно ![]() различных булевых функций от n переменных.
различных булевых функций от n переменных.
Следует отметить, что здесь и далее к числу функций от n переменных относятся и такие функции f(x1, x2, . . ., xn), которые не зависят от тех или иных переменных xi. В частности, в числе функций окажутся функции – константы (тождественная истина и тождественная ложь), которые можно рассматривать как функции от нуля переменных.
Условимся называть невырожденными функциями от n переменных такие функции, которые существенно зависят от всех этих переменных. Функции же от n переменных, сводящиеся к функциям от меньшего числа переменных называются вырожденными.
В теории булевых функций особое значение имеют функции одной и двух переменных. Имеется всего ![]() = 4 разных функций одной переменной.
= 4 разных функций одной переменной.
| x f | G1 | G2 | G3 | G4 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
G1, G4 – константы 0 и 1.
G2 = x.
![]() и называется функцией отрицания или инверсии.
и называется функцией отрицания или инверсии.
Число булевых функций от двух переменных равно ![]() . Выпишем сводную таблицу всех этих функций.
. Выпишем сводную таблицу всех этих функций.
| x | y | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Из выписанных функций шесть будут вырожденными, а именно функции F1, F4, F6, F11, F13, F16. Действительно, легко видеть:
![]()
Остальные функции будут невырожденными. Введем для них специальные названия и обозначения.
Функция F2 носит название конъюнкции или произведения или логического И. Для ее обозначения используется либо знак умножения, либо Ù. Отсюда:
![]()
Функция F7 носит название функции неравнозначности или суммы по модулю два. Для ее обозначения будем использовать:
![]()
Функция F8 носит название дизъюнкции или логическое ИЛИ. Для ее обозначения принято использовать знак Ú:
![]()
Функцию F9 будем называть отрицанием дизъюнкции или стрелкой Пирса, и обозначать через:
![]()
Функция F10 носит название функции равнозначности или эквивалентности и обозначается:
![]()
Функции F12 и F14 носят название импликации. Для их обозначения будем использовать:
![]()
Здесь следует отметить, что импликация соответствует высказыванию «Если А, то В». При этом возникает ситуация, что это высказывание с ложным А и истинным В истинно. Прежде всего, это соглашение, причем это соглашение ничему не противоречит. В повседневном языке утверждения с ложным А не употребляются.
Пример типа «Если бы я был космонавтом, я бы полетел на Луну» не опровергает наше утверждение. Здесь 1. Имеем дело не с «Если А, то В», а с «Если бы А, то бы В»; 2. Считать ложным такое утверждение не имеет смысла.
Возникает вопрос, можно ли бы было при ложном А, считать ложным высказывание «Если А, то В». В принципе можно, но математическая практика показывает, что выбранный нами вариант удобнее.
Приведем пример. Известно, что при возведении в квадрат обоих частей уравнения могут появиться новые корни. При этом подразумевается, что при возведении в квадрат корни потеряться не могут. Что это значит. Это значит, что любой корень уравнения:
![]()
является также корнем уравнения
![]()
Это высказывание мы считаем верным, хотя исходное уравнение может вовсе не иметь корней. Ясно, что здесь мы использовали введенное соглашение.
Функция F15 носит название отрицание конъюнкции или штрих Шеффера. Для ее обозначения используется:
![]()
Оставшиеся функции F3 и F5 назовем отрицание импликации:
![]()
Для построения исчисления высказываний важным является вопрос о построении функционально полной системы функций.
Будем говорить, что система логических функций называется функционально полной, если существует алгоритм, позволяющий строить из этих функций любые наперед заданные функции. Функционально полная система называется несократимой, если исключение какой-либо входящей в нее функции лишает систему свойства функциональной полноты.
Можно показать, что: Максимальное число функций в несократимой функционально полной системе булевых функций от двух переменных равно четырем. Таким образом, для булевой алгебры можно построить несколько вариантов функционально полных систем. В частности, стрелка Пирса и штрих Шеффера каждый по отдельности составляют функционально полную систему. Однако наиболее часто в качестве функционально полной системы используются: отрицание, конъюнкция и дизъюнкция.
Функции F7, F9, F15, F5, F3 уже выражены через эти операции. Выразим функции F10, F12, F14.
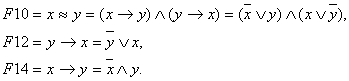
Фактически значение любой функции можно получить по таблице ее истинности. Однако, это значение можно получить, представив функции булевой алгебры с помощью алгебраических функций.
Алгебраически перечисленные выше операции можно выразить следующим образом:
Отрицание (дополнение): ![]()
Конъюнкция: ![]()
Дизъюнкция: ![]()
Тогда:
Сумма по модулю 2: ![]()
Стрелка Пирса: ![]()
Эквивалентность: ![]()
Импликация: ![]()
Штрих Шеффера: ![]()
Отрицания импликации: ![]()
Отметим, что эти формулы справедливы для бесконечнозначных и многозначных логик.
Законы булевой алгебры.
Для удобства разобьем законы на четыре группы.
Первая группа.
1. ![]() (закон коммутативности для дизъюнкции).
(закон коммутативности для дизъюнкции).
2. ![]()
3. ![]() (первый закон поглощения).
(первый закон поглощения).
4. ![]() (второй закон дистрибутивности).
(второй закон дистрибутивности).
5. ![]() (закон идемпотентности для дизъюнкции).
(закон идемпотентности для дизъюнкции).
Следующие пять законов получаются заменой Ù на Ú и наоборот.
1¢. ![]() (закон коммутативности для конъюнкции).
(закон коммутативности для конъюнкции).
2¢. ![]() (закон ассоциативности для конъюнкции).
(закон ассоциативности для конъюнкции).
3¢. ![]() (второй закон поглощения).
(второй закон поглощения).
4¢. ![]() (первый закон дистрибутивности)
(первый закон дистрибутивности)
5¢. ![]() (закон идемпотентности для конъюнкции).
(закон идемпотентности для конъюнкции).
Каждый из законов 1¢ - 5¢ называется двойственным к соответствующему закону 1 – 5.
Вторая группа1. ![]()
![]()
2. ![]()
![]()
![]()
3. ![]()
![]()
4. ![]()
![]()
5. ![]()
![]()
6. ![]()
![]()
1. ![]() (закон двойного отрицания).
(закон двойного отрицания).
2. 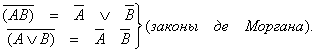
3. ![]()
1. ![]()
2. ![]() (закон контрапозиции).
(закон контрапозиции).
3. ![]()
Сформулируем некоторые полезные следствия из приведенных законов.
С1. Выбрасывая из произвольной дизъюнкции дизъюнктивные элементы равные нулю, мы не изменим величину этой дизъюнкции.
С2. Если в дизъюнкции хотя бы один из элементов равен 1, то вся дизъюнкция равна 1.
С3. Выбрасывая из произвольной конъюнкции все сомножители равные 1, мы не изменим ее величины.
С4. Если в конъюнкции хотя бы один сомножитель равен 0, то все произведение равно 0.
С5. Дизъюнкция или произведение любого числа одинаковых элементов равняется А.
Эти следствия можно доказать по индукции.
С6. Если А(а1, . . ., ап) произвольное выражение булевой алгебры, построенное из выражений а1, . . ., ап с помощью операций отрицания, дизъюнкции и конъюнкции, то отрицание этого выражения равняется ![]() , где В(а1,…,ап) получается из А с помощью замены всех умножений на дизъюнкции, а всех дизъюнкций на умножения, при условии сохранения всех имевшихся в А отрицаний.
, где В(а1,…,ап) получается из А с помощью замены всех умножений на дизъюнкции, а всех дизъюнкций на умножения, при условии сохранения всех имевшихся в А отрицаний.
С7. Если к некоторому выражению А булевой алгебры применено более чем одно отрицание, то, не меняя значения выражения, можно исключить любое четное число отрицаний.
Нормальные формыЭлементарной дизъюнкцией называется выражение,![]() представляющее собой дизъюнкцию любого конечного множества попарно различных между собой переменных, часть которых (возможна пустая) взята со знаком отрицания. К числу элементарных дизъюнкций будем также относить выражения, состоящие из одной переменной (с отрицанием или без), а также константу 0.
представляющее собой дизъюнкцию любого конечного множества попарно различных между собой переменных, часть которых (возможна пустая) взята со знаком отрицания. К числу элементарных дизъюнкций будем также относить выражения, состоящие из одной переменной (с отрицанием или без), а также константу 0.
В силу определения: ![]()
являются элементарными дизъюнкциями, а ![]() не являются.
не являются.
Элементарным произведением называется выражение, представляющее собой произведение любого конечного множества попарно различных между собой переменных, над частью которых (быть может пустой) поставлен знак отрицания. К числу элементарных произведений также относятся выражения с одной переменной с отрицанием или без, а также константа 1. Элементарные произведения: ![]() Неэлементарные произведения:
Неэлементарные произведения: ![]() Переменные и их отрицания называются первичными термами или литералами.
Переменные и их отрицания называются первичными термами или литералами.
Дизъюнкция любого числа первичных термов равна либо 1, либо элементарной дизъюнкции. Произведение любого числа первичных термов равно либо 0, либо элементарному произведению.
Нормальной дизъюнктивной формой (ДНФ) называется дизъюнкция любого конечного множества попарно различных произведений.
Конъюнктивной нормальной формой (КНФ) называется произведение любого конечного множества попарно различных дизъюнкций.
Алгоритм приведения к ДНФ и КНФ заключается в следующем.
Похожие работы
... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п. Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...
... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники 1. Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...
... набор процедур и функций языков программирования Basic и Pascal, позволяют управлять графическим режимом работы экрана, создавать разнооборазные графические изображения и выводить на экран текстовые надписи. ГЛАВА 2. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ ЯЗЫКА ПРОГРАММИРОВАНИЯ В КУРСЕ ИНФОРМАТИКИ БАЗОВОЙ ШКОЛЫ (НА ПРИМЕРЕ BASIC И PASCAL) 2.1 Разработка мультимедиа курса «Графические возможности языков ...
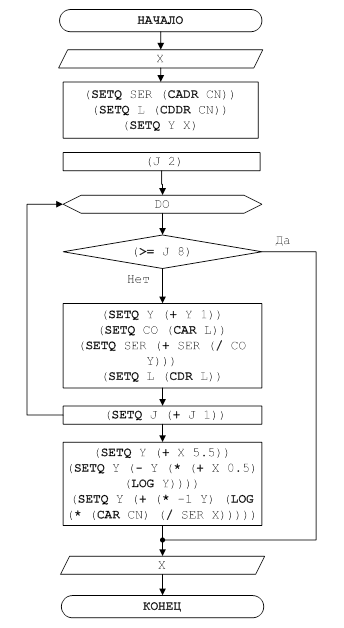
... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...
0 комментариев