Навигация
Практические задания
3.4.1 Практические задания
1.Создать машинное представление для списков:
(a (b c) ( (d) e (f)))
( + a (* b (/ (+ c (/ d e)) f)))
(/ (+ ( a (- (b c)))) (* (/ (d b)) a))
(flat (hd (a) flat (tl (a) b)))
(cons (copy (hd (l) )) copy (tl (l)))))
2.Определить значения списков:
(car ‘(a (b c) ((d) e (f))))
(cdr ‘(a (b c) ((d) e (f))))
(cdadr ‘(a (b c) ((d) e (f))))
(cons nil ‘(суть пустой список))
(cons (car ‘(a b))(cdr ‘(a b)))
(car ‘(car (a b c)))
(cdr (car (cdr ‘(a b c))))
3.Запишите последовательность вызовов CAR и CDR, выделяющих из приведенных списков символ «цель». Упростите эти последовательности с помощью функций C…R.
(1 2 цель 3 4)
((1) (2 цель ) (3 4 цель)))
((1 (2 (3 4 цель))))
4.Определить вид списка, имеющего следующее машинное представление:
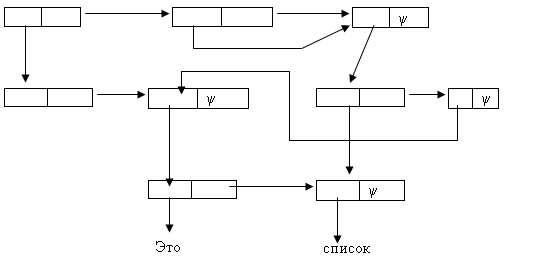
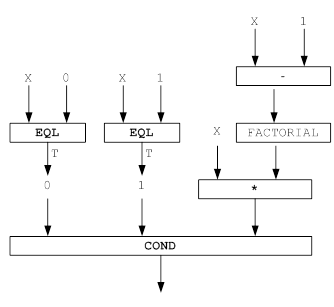
4. Реализовать с помощью COND логические операции: эквивалентность, штрих Шеффера, стрелка Пирса.
5. Реализовать функцию reverse, переставляющую местами элементы списка.
3.4.2 Компьютерное задание
Создать БД для индуктивного вывода и реализовать программу заполнения этой базы для оператора Setq. Возможная структура таблицы для хранения списков:
| Имя поля | Тип | Комментарий |
| List | Text | Наименование списка |
| BeginList | Boolean | Является ли началом списка, если да -TRUE |
| SonPointer | Long | Указатель на сына |
| BrotherPointer | Long | Указатель на брата |
| ValueEl | Text | Значение. Для указателей Nil |
| ValueType | Text | Тип значения: ячейка, список, пустой список, атом, функция |
Пример заполнения:
Пусть последовательно создаются 2 списка:
Setq a (* (+ 2 3) c)
Setq Second ((a) (b))
Структура списков: Список а

Список Second
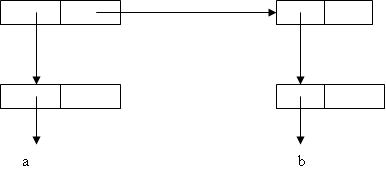
Таблица для этих списков будет иметь вид:
| List | BeginList | SonPointer | Brother Pointer | ValueEl | ValueType |
| a | true | 2 | 4 | Nil | ячейка |
| a | false | 3 | 0 | Nil | ячейка |
| a | false | 0 | 0 | * | функция |
| a | false | 5 | 11 | Nil | ячейка |
| a | false | 6 | 7 | Nil | ячейка |
| a | false | 0 | 0 | + | функция |
| a | false | 8 | 9 | Nil | ячейка |
| a | false | 0 | 0 | 2 | атом |
| а | false | 10 | 0 | Nil | ячейка |
| а | false | 0 | 0 | 3 | атом |
| а | false | 12 | 0 | Nil | ячейка |
| a | false | 0 | 0 | c | Пустой список |
| Second | true | 14 | 16 | Nil | ячейка |
| Second | false | 15 | 0 | Nil | ячейка |
| Second | false | 0 | 0 | a | список |
| Second | false | 17 | 0 | Nil | ячейка |
| Second | false | 18 | 0 | Nil | ячейка |
| Second | false | 0 | 0 | b | Пустой список |
Порядок выполнения
1. Создание таблиц и форм для ввода и хранения списков (1 занятие).
2. Реализация алгоритмов преобразования описания списка в машинное представление и обратно (2 занятия).
3. Реализация операций над списками (2 занятия)
4. Реализация алгоритма Eval (2 занятия).
5. Оформление результатов (1 занятие).
4. Логическое программирование
Логическое программирование основывается на представлении задач в виде теорем, доказываемых в рамках исчисления предикатов первого порядка.
4.1 Модели и опровержения
В доказательстве теорем стараются показать, что определенная ППФ B есть логическое следствие множества ППП S = {A1, …, An}, называемых аксиомами рассматриваемой задачи. Правило вывод есть правило, при помощи которого из ранее полученных выражений можно получить новое. Например, если Ai и Aj истинные ППФ, то запись:
![]()
указывает, что Ak можно получить из Ai и Aj с помощью правила fq . Рассмотрим последовательность S(0), …, S(j+1), образованную из некоторого множества аксиом S по правилу:
S(0) = S,
…
S(j+1) = S(j) È F(S(j),
где F(S) – множество выражений, которое можно получить из множества S, применяя к каждому его элементу все возможные правила fq из конечного множества F={fq}. Говорят, что высказывание B следует из аксиом, принадлежащих S, если B Î S(j) для некоторого j.
Напомним, что терм – это константа, переменная или функция. В качестве своих аргументов n – местная функция должна иметь п термов. Таким образом, термами будут: a, b, c, f(a), g(f(x), y).
Атомом называется предикат со своими аргументами. Литерал – это атом или его отрицание. Предложение C – это дизъюнкция литералов. Множество предложений S интерпретируется как единое высказывание, представляющее конъюнкцию всех его предложений.
Как уже отмечалось, высказывание T следует из множества предложений S, если T есть логическое следствие предложений из S. Предположим для простоты, что T состоит из единственного предложения. Рассмотрим множество предложений:
![]()
Для того, чтобы высказывания SÈT были истинными, все предложения Ci и T должны быть истинными. В свою очередь значения истинности этих предложений будут определяться значениями истинности, содержащихся в них атомов, причем значения истинности должны присваиваться атомам так, чтобы, по крайней мере, один литерал в каждом предложении был истинным.
Отдельное присваивание истинности атомам называется моделью. Если S влечет за собой T, то не существует модели, в которой S истинное, а T – нет. Вместе с тем, если высказывание T истинное, то его отрицание должно быть ложным. Поэтому, если S влечет за собой T, высказывание:
![]() (1)
(1)
должно быть ложным для любой модели.
Этот же вывод можно сделать следующим образом:
![]()
и от противного:
![]()
Предположим, что число атомов конечно. Тогда существует конечное множество моделей, так как k атомам можно присвоить логические значения 2k различными способами. Очевидно, что присваивать значения этим комбинациям можно последовательно и если для всех моделей (1) окажется ложным, то, безусловно, S влечет T. Такое доказательство называется методом от противного и составляет основу методов доказательства теорем.
Доказать противоречивость (1), если число атомов конечно, достаточно просто. Просто ли это на практике зависит от количества атомов и от возможности порождать и проверять модели.
Возникает задача выявления условий, гарантирующих конечное число атомов. Пусть S – это множество высказываний истинных для тех атомов, которые непосредственно входят в S и тех, которые из них можно вывести. Последнее множество может быть бесконечным. В этом можно убедиться на следующем примере. Пусть S – высказывание, содержащее единственный атом S = {R(a, x)}.
Предположим, что определена функция g(x). Тогда можем построить бесконечную последовательность R(a, x), R(a, g(x)), R(a, g(g(x))), … . Эта последовательность перечислимая, так как можно придумать схему перечисления, по которой упорядочиваются высказывания. Например, по уровню вложенности второго аргумента. Можно показать, что всегда можно построить схему перечисления бесконечного множества атомов, полученного из конечного при помощи некоторой подстановки.
Предположим, что S не содержит переменных. Такая ситуация называется основным случаем, а соответствующий универсум (область определения) Эрбрановой базой. В основном случае можно провести перечисление.
Докажем, например, для конкретной пары чисел (a, b) (но не для произвольной пары чисел вообще x, y) истинность высказывания:
a = b ® a > b.
Аксиомами будут:
A1: a > b,
A2: a < b,
A3: a = b.
Соответствующие предложения будут иметь вид:
![]() - выполняется одно из отношений;
- выполняется одно из отношений;
 - одновременно не выполняются никакие два отношения.
- одновременно не выполняются никакие два отношения.
В этих обозначениях наше утверждение имеет вид:
![]()
и его отрицание A3A1. Отсюда получим:
![]()
Обозначим ![]()
Так как в S может быть только 23 = 8 атомарных высказываний, легко построить все возможные модели. Если для каждой из них хотя бы одно предложение в S принимает значение ложь, то высказывание вида (1) будет ложным, и поэтому наше утверждение будет истинным.
| Модель | Предложения, которым присваивается значение ложь |
| A1, A2, A3 | C2, C3, C4 |
|
|
|
|
| C3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Теорема Эрбрана – Сколема – Геделя. В этой теореме утверждается, что можно найти частичное присваивание, приписывающее значение ложь любому противоречивому множеству предложений.
Теорема Эрбрана – Сколема – Геделя. В этой теореме утверждается, что можно найти частичное присваивание, приписывающее значение ложь любому противоречивому множеству предложений.
Похожие работы
... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п. Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...
... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники 1. Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...
... набор процедур и функций языков программирования Basic и Pascal, позволяют управлять графическим режимом работы экрана, создавать разнооборазные графические изображения и выводить на экран текстовые надписи. ГЛАВА 2. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ ЯЗЫКА ПРОГРАММИРОВАНИЯ В КУРСЕ ИНФОРМАТИКИ БАЗОВОЙ ШКОЛЫ (НА ПРИМЕРЕ BASIC И PASCAL) 2.1 Разработка мультимедиа курса «Графические возможности языков ...
... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...
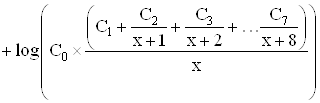
0 комментариев