Если для всех xÎM F оценивается как истина, то истиной является ("x)F(x)

2.         Если для всех xÎM F оценивается как истина, то истиной является ("x)F(x).

3.         Если хотя бы для одного xÎM F оценивается как истина, то ($x)F(x) тоже истина.

Предложения

Когда все переменные предиката являются связанными, то такой предикат называется предложением. Различие между ППФ, являющимися и не являющимися предложениями, состоит в том, что предложениям можно однозначно поставить в соответствие значение True или False, в то время как во втором случае нельзя непосредственно по виду формулы вынести суждение об ее истинности или ложности. Например, предикатная формула подсистема (x, y) не является предложением. Если в нее подставлены определенные значения, например, x = процессор, y = ЭВМ, то выражение подсистема (процессор, ЭВМ) принимает значение True, а при подстановке x = человек, выражение подсистема(человек, ЭВМ) является False. То есть истинность или ложность предикатной формулы можно оценить тогда и только тогда, когда в переменные подставлены некоторые конкретные сущности (в этом случае формула называется высказыванием). Отметим, что значение предикатных формул со связанными переменными можно определить, и не производя такого рода подстановки.

Например,  - у каждого человека имеется отец – является истиной, а  - любой является чьим-то отцом – является ложью.

Предположим, что имеется некоторое множество логических формул S. Если существует такая интерпретация, что все эти формулы принимают значение истина, то подобная интерпретация называется моделью. Например, рассмотрим множество:

Тогда интерпретация вида (человек (Сократ) = True) и (смертен (Сократ) = True) – является моделью так как все логические формулы S есть истина. Не обязательно, что такая модель единственна.

Пусть имеется некоторая группа S логических формул. Если для всех моделей S некоторая логическая формула s есть истина, то принято говорить, что s является логическим заключением (консеквентом) в S. Факт реализации логического консеквента записывается в виде S½=s.

Правила вывода логики предикатов

Вывод представляет собой процедуру, которая из заданной группы выражений выводит, отличное от заданного выражение. Когда группа выражений, образующих посылку, является истиной, то должно гарантироваться, что выражение, выведенное из них в соответствии с правилом вывода, также является истиной.

В логике предикатов в качестве такого правила вывода используется правило, которое из двух выражений A и A®B выводит новое выражение B. Это правило называется правилом дедуктивного вывода.

Для описаний правил вывода во многих случаях используется нотация (как это указывалось выше), при которой над чертой записывается группа выражений, принимаемых за посылку, а под чертой – выражение, которое выводится:

Такой тип правила вывода носит название modus ponens.

Можно многократно использовать одно и тоже правило вывода. Например, если помимо выражений A, A®B существует выражение B®C, то можно вывести C, дважды использовав приведенное правило. Получение выражения s применением конечного числа раз правила вывода к заданной группе выражений S будем записывать в виде:

При этом говорят, что s дедуктивно выводится из S. Очевидно, что из вышеуказанного, легко выводится еще одно правило:

Практические задания

Задание 1. Задан предикат выполнение(x, y) , который задает отношение «y является результатом выполнения программы x». Дать интерпретацию утверждений:

("x)($y)выполнение(x,y);

($x)("y) выполнение(x,y);

("x)("y) выполнение(x,y);

($x)("y) выполнение(x,y);

("y)($x) выполнение(x,y);

($x)($y) выполнение(x,y).

Задан предикат реализация(x, y), который означает «программа x реализована на языке y». Записать утверждения:

А) Существует программа, реализованная на Паскале, имеющая в качестве результата 1000.

Б) Любая программа, написанная на C, дает результат.

3. Функциональное программирование

Функциональное программирование представляет собой модель индуктивного вывода, реализуемую с помощью рекурсивных процедур, l-исчисления и списковых структур.

3.1 Индуктивный вывод

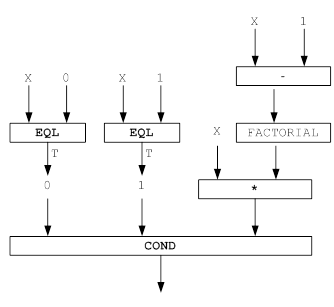
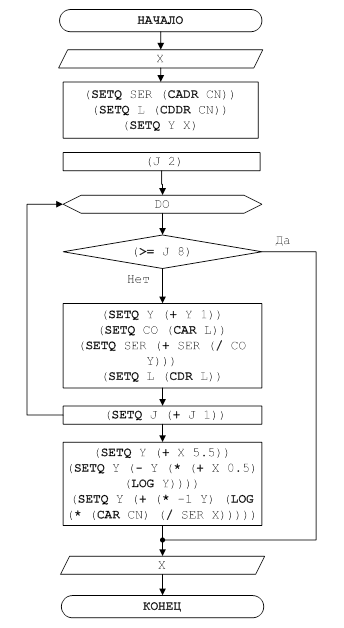
Индуктивный вывод – это вывод из имеющихся данных, объясняющего их общего правила. Например, пусть известно, что есть некоторая функция от одной переменной. Рассмотрим как выводится f(x), если последовательно задаются в качестве данных пары значений (1, f(0)), (1, f(1)). Вначале задается (0, 1) и имеет смысл ввести постоянную функцию f(x) = 1. Затем задается пара (1, 1), которая удовлетворяет f(x)=1. Следовательно, нет необходимости менять вывод. Пусть теперь задается (2, 3). Это не согласуется с нашим выводом. Предположим, что методом проб и ошибок удается найти . Она удовлетворяет заданным до сих пор фактам. Далее, если будут следовать факты (3, 7), (4, 13), (5, 21), …, убедимся в справедливости предшествующего вывода. Таким образом в индуктивном выводе в каждый момент времени объясняются все данные, полученные до этого момента. Если данные, позже, перестанут удовлетворять полученному выводу, то его придется менять. Следовательно, индуктивный вывод – это неограниченно долгий процесс.

Для определения индуктивного вывода необходимо уточнить:

1.   Множество правил объектов вывода.

2.   Метод представления правил.

3.   Способ показа примеров.

4.   Метод вывода.

5.   Критерий правильности вывода.

В качестве правил – объектов вывода можно рассматривать:

-                 функции;

-                 грамматики языков;

-                 программы.

Метод представления удобно организовывать в виде пар (x, f(x)), последовательности действий, вычисляющих f(x) и т.д.

Вывод реализуется благодаря неограниченному повторению процесса:

Запрос входных данных ® предположение ® выходные данные.

Критерием правильности вывода считается идентификация в пределе. Говорят, что машина вывода M идентифицирует в пределе правило R, если при показе примеров правилу R последовательность выходных данных, генерируемых M, сходится к некоторому представлению t, а именно: все выходные данные, начиная с некоторого момента времени, совпадают с t, при этом t называют правильным представлением R. Кроме того, говорят, что множество правил G позволяет сделать индуктивный вывод, если существует некоторая машина вывода M, которая идентифицирует в пределе любое правило R из множества G.

Характерным примером индуктивного вывода является математическая индукция.

Похожие работы

Общая терминология программирования

Скачать

71422

1

0

... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п.   Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...

Программирование и достижения компьютерной техники

Скачать

60551

0

0

... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники   1.         Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...

Графические возможности программирования в курсе информатики

Скачать

110612

10

19

... набор процедур и функций языков программирования Basic и Pascal, позволяют управлять графическим режимом работы экрана, создавать разнооборазные графические изображения и выводить на экран текстовые надписи. ГЛАВА 2. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ ЯЗЫКА ПРОГРАММИРОВАНИЯ В КУРСЕ ИНФОРМАТИКИ БАЗОВОЙ ШКОЛЫ (НА ПРИМЕРЕ BASIC И PASCAL)   2.1 Разработка мультимедиа курса «Графические возможности языков ...

Функциональное и логическое программирование

Скачать

11287

1

10

... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...