Практические задания

3.3.1 Практические задания

1.Определить функцию f(x, y) = iif(x>y, sin(x), cos(x)) в l - исчислении. Дать ее запись для x=t и y=p/2. Осуществить редукцию.

2.Осуществить редукцию следующих l - выражений:

lf.[lg.[lt.[f(g(x)+t(y)]]](sin, cos, tg),

lg.[lt.[lf.[f(g(x)+t(y)]]](sin, cos, tg),

lf.[lt.[lg.[f(g(x)+t(y)]]](sin, cos, tg),

3.4 Использование списков

Введем некоторые определения. Символ - это набор букв, цифр и специальных знаков. Кроме символов будем использовать: числа, Т – истина, Nil – ложь или пустой список. Будем понимать под константами – числа, Т, Nil. Будем понимать под атомами символы и числа. Назовем списком упорядоченную последовательность, элементами которой являются атомы или другие списки (подсписки). Будем заключать списки в круглые скобки, а элементы списка разделять пробелами.

Формально список можно определить следующим образом:

Список :- Nil / (голова Ç хвост)

[Список либо пуст, либо это пара голова и хвост]

голова :- атом / список

[рекурсия в глубину]

хвост :- список

[рекурсия в ширину]

Другой вариант определения:

Список :- Nil / (элемент элемент … )

Элемент :- атом / список

[рекурсия]

Обратим внимание, что атом это не список, хотя символ может идентифицировать список. Каждый символ имеет значение. Им может быть список, в том числе и пустой, константа, функция, которую рассматривают как специальный символ. Для записи функций будем использовать префиксную нотацию, т.е. x + y будем записывать, как (+ x y).

Атомы и списки будем называть S – выражениями.

Для представления списков будем использовать совокупность ячеек памяти, каждая из которых содержит два указателя. Первый указатель играет роль указателя на сына, второй – на брата. Например, список (А В) будет иметь вид.

Отсутствие указателя будем обозначать символом y.

Список (* (+ 2 3) с) будет иметь представление:

Чтобы определить выражение по его машинному представлению, нужно просматривать представление, следуя указателям, расположенным слева, на наибольшую глубину и затем по правым указателям (внешний просмотр).

При записи выражения каждой стрелке, не заканчивающейся на атоме, соответствует открывающаяся скобка, каждому символу y - закрывающаяся скобка, каждому атому – сам атом.

Этой схеме соответствует список ((А)(В)).

Вернемся к определению атома. Фактически атомы являются функциями, аргументы которых представляют собой следующие за ними S – выражения. В свою очередь аргумент сам может быть функцией, которую надо вычислить. Поэтому возникает необходимость определять, что представляет собой данный элемент: значение выражения L или символьное имя L какого-то S – выражения. В первом случае перед выражением ставится‘ или указатель QUOTE. Апостроф запрещает вычисление следующего за ним S - выражения, которое воспроизводится без изменений.

Для задания выражений введем функцию Setq:

(Setq <атом> <S – выражение>)

(Setq <атом> ‘<S – выражение>)

В первом случае выражение должно быть вычислено, во втором – на вычисляется. Кроме того, Setq связывает полученный результат с атомом.

(Setq L1 (+ 4 5))

(Setq L1 ‘(+ 4 5))

В первом случае L1 связано с (9), во втором – с (+ 4 5).

Функция CAR возвращает в качестве значения первый элемент списка, то есть его голову. Функция имеет смысл, только для аргументов, являющихся списками, имеющими голову.

(CAR ‘ (A B C)) ® A

(CAR ‘ A) ® ошибка, А не список.

Функция CDR возвращает хвост списка. Если список состоит из одного элемента, то результатом является Nil.

(CDR ‘ (A B C)) ® (B C)

Комбинация вызовов CAR и CDR выделяет произвольный элемент списка. Для простоты эту комбинацию записывают в виде:

(C…R список)

Вместо многоточия записывается комбинация из букв А (для CAR) и D (для CDR).

(CADDAR L) = (CAR (CDR (CDR (CAR L))))

Функция CONS строит новый список из переданных ему головы и хвоста.

(CONS голова хвост)

(CONS ‘a ‘(b c)) ® (a b c)

(CONS ‘(a b) ‘(c d)) ® ((a b) c d)

(CONS (+ 1 2) ‘(+ 4)) ® (3 + 4)

Здесь первый аргумент без апострофа, поэтому берется как значение.

(CONS ‘(+ 1 2) ‘(+ 4)) ® ((+ 1 2) + 4)

(CONS ‘(a b c) Nil) ® ((a b c))

(CONS Nil ‘(a b c)) ® (Nil a b c)

Предикат ATOM используется для анализа списков, а именно, для идентификации является ли объект атомом или нет.

(ATOM ‘x) ® T

(ATOM (CDR ‘(A B C))) ® Nil. Атом от списка (B C) естественно False.

(ATOM (ATOM (+ 2 3))) ® T.

Результат сложения чисел атом. Т также является атомом.

(EQUAL <S-выр1> <S-выр2>) ® T, если и только если значения обоих выражений равны.

(EQ <S-выр1> <S-выр2>) ® T, если и только если значения обоих выражений равны и представляют один физический список.

(AND <S-выр1> <S-выр2> … <S-вырn>) – если встречается Nil,, возвращается Nil, иначе значение последнего выражения.

(OR <S-выр1> … <S-вырn>) – если при просмотре встречается выражение отличное от Nil, то оно возвращается, иначе Nil.

(NOT <S-выр>) ® T, если и только если значение выражения есть Nil.

Определять функции будем согласно l - исчислению.

(l (x₁, x₂, …, x_n) f)

x_i – формальный параметр.

f – тело функции.

Например, функция вычисляющая сумму квадратов будет определяться следующим образом:

(l (x y) (+ (* x x) (* y y))).

Чтобы произвести вычисления будем осуществлять l - вызов.

(l - выражение a₁, …, a_n),

Здесь a_i – форма , задающая фактические параметры.

((l (x y) (+ (* x x) (* y y))) 2 3) - дает 13.

Для того чтобы определить новую функцию будем использовать запись:

(DEFUN <имя> <l - выражение>).

Для удобства исключим значок l и внешние скобки.

(DEFUN проценты (часть целое) (* (/ часть целое) 100)).

Вызов:

(проценты 4 20)

Результат: 20.

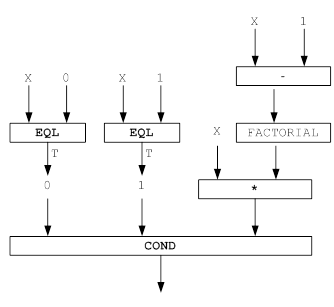
Условное выражение COND имеет следующий вид:

(COND (p1 a1)

(p2 a2)

. . .

(pn an))

Значение COND определяется следующим образом:

1.         Выражения pi вычисляются последовательно слева направо (сверху вниз) до тех пор, пока не встретится выражение, значение которого отлично от Nil.

2.         Вычисляется результирующее выражение ai соответствующее этому pi и полученное значение возвращается в качестве результата.

3.         Если нет ни одного pi, значение которого отлично от Nil, то значение COND равно Nil/

В более общем виде:

(COND (p1 a1)

…

(pj)

…

(pk ak₁ … ak_n)

…)

В этом случае:

-           если условию не ставится в соответствие результирующее выражение, то в качестве результата при истинности предиката выдается само значение предиката;

-           если условию соответствует несколько S – выражений, то при его истинности они вычисляются слева направо и результатом будет значение последнего S – выражения.

Реализуем логические связки И, ИЛИ, ®.

(defun И(x y) (COND (x y) (T Nil)))

(defun ИЛИ (x y) (COND (x T) (T y)))

(defun ® (x y) (COND (x y) (T T)))

С помощью COND можно реализовать различные варианты условных выражений.

(if <условие> <то-выр> <иначе-выр>) º (COND (<условие> <то-выр>) (T <иначе-выр>))

Чтобы говорить о некотором свойстве, связанным с некоторым объектом и его значением, будем использовать функцию:

(PUTPROP <атом1> <список> <атом2>).

Эта функция связывает свойства, выраженные списком <атом2>, с конкретным объектом с именем <атом1>. Конкретные значения свойства задаются в объекте <список>.

(PUTPROP ‘Петр ‘(Иван Ирина) ‘Дети).

Чтобы узнать обладает ли объект данным свойством, будем использовать функцию GET:

(GET <атом1> <атом2>) ® значение свойства.

(GET ‘Петр ‘Дети) ® (Иван Ирина)

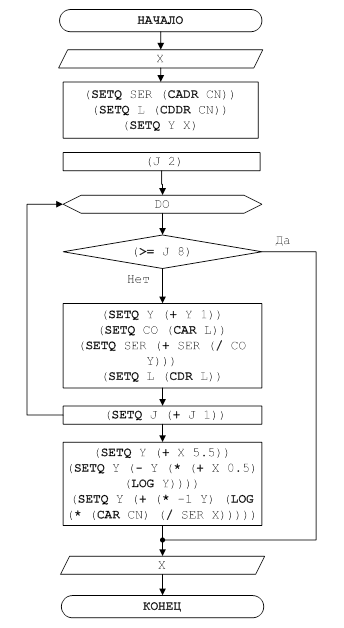
Теперь сформулируем алгоритм для вычисления списков. Алгоритм должен вычислять значение списка в последовательности, задаваемой указателями – «сыновьями», а затем учитывается последний из встреченных указателей «братьев». После этого учитываются указатели «сыновья», связанные с этим последним, и так далее, пока не получается окончательное значение для данной ветви. Затем вычисления повторяются снова, охватывая выражения более высокого уровня, и так до тех пор пока не будет определено значе ние всего списка. Те части всего выражения, которые ожидают вычисления значений их аргументов, называются квазарами.

Этот алгоритм представим в вида процедуры Eval(S), где S – выражение.

Sub Eval(S)

If S есть атом then

Возврат ¬ значение S

Else

If S1 = QUOTE then

Возврат ¬ S2

Else

S1 есть функция

If S1 указывает на специальную обработку, выполнить эту обработку

Else

Применить Eval ко всем элементам S2 последовательно и затем рекуррентно использовать их найденные значения.

Окончательный возврат ¬ S1 (Eval (S2))

End If

End If

End If

S1 – первый сын для S. S2 – элементы выражения S, представляющие собой множество братьев выражения S1.

Похожие работы

Общая терминология программирования

Скачать

71422

1

0

... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п.   Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...

Программирование и достижения компьютерной техники

Скачать

60551

0

0

... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники   1.         Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...

Графические возможности программирования в курсе информатики

Скачать

110612

10

19

... набор процедур и функций языков программирования Basic и Pascal, позволяют управлять графическим режимом работы экрана, создавать разнооборазные графические изображения и выводить на экран текстовые надписи. ГЛАВА 2. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ ЯЗЫКА ПРОГРАММИРОВАНИЯ В КУРСЕ ИНФОРМАТИКИ БАЗОВОЙ ШКОЛЫ (НА ПРИМЕРЕ BASIC И PASCAL)   2.1 Разработка мультимедиа курса «Графические возможности языков ...

Функциональное и логическое программирование

Скачать

11287

1

10

... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...