По различию используемых символов

1.   По различию используемых символов.

2.   По существованию НОУ для двух выражений, в которых удалены одинаковые символы.

Далее все делается рекуррентно.

Пример 1. Милиция разыскивает всех въехавших в страну, за исключением дипломатов. Шпион въехал в страну. Однако, распознать шпиона может только шпион. Дипломат не является шпионом.

Оценим вывод: среди милиционеров есть шпион.

Воспользуемся следующими предикатами:

Въехал(x): x въехал в страну.

Дипломат(x): x – дипломат.

Поиск(x, y): x разыскивает y.

Милиционер(x): x – милиционер.

Шпион(x): x – шпион.

Если выразим через эти предикаты посылку и вывод в форме ППФ, то получим:

для всех x, если x не является дипломатом, но въехал в страну, найдется милиционер y, который его разыскивает.

Если существует шпион x, который въехал в страну, и некоторый y разыскивает его, то он сам шпион.

Для всех x справедливо, что если x является шпионом, то он не дипломат.

Заключение:

Существует x такой, что он является шпионом и милиционером.

Если эти формулы преобразовать в клаузальную нормальную форму, то получим:

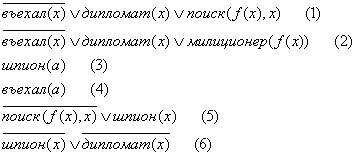
Заключение преобразуем в свое отрицание:

и затем в клаузальную форму без квантора общности.

Последующий процесс доказательства имеет вид:

дипломат(а)Úмилиционер(f(а)) [a/x] из 2,4 (9)

милиционер(f(а)) [a/x] из 8,9 (10)

дипломат(а)Úпоиск(f(а),а) [a/x] из 1,4 (11)

поиск(f(а),а) [a/x] из 8,11 (12)

шпион(f(a)) [a/x] из 12,5 (13)

ð [f(a)/x)] из 10 и 14 (15)

Еще одной возможностью метода резолюции является возможность получать конкретные значения переменных, содержащихся в заключении.

4.2.3.3 Задачи, использующие равенства

Новые предложения получались до сих пор двумя способами: подстановкой и резолюцией. При резолюции пары предложений, отображаются в новые предложения, а подстановка заменяет терм в предложении другим термом той же синтаксической формы. Иногда возникает необходимость заменить терм равным ему термом, который не является термом, для которого возможна подстановка (подстановочным случаем) в первом терме. Рассмотрим простой пример. Положим f(x, y) = x + y. При сравнении предложений:

у нас нет способа обнаружить противоречие, поскольку резолюция не допускает замены термов разных синтаксических форм. Поэтому имеет смысл, включить в программу, использующую принцип резолюции, специальные правило вывода, которое должно применяться, когда возникает необходимость в операции равенства. Чтобы это правило было совместимо с остальной частью программы, оно должно удовлетворять двум условиям:

1.   Работать с предложениями, в которых равенство выражено в виде атомов.

2.   Быть операцией, превращающей два предложения в третье.

Это специальное правило вывода называется парамодуляцией.

Пусть A, B и т.д. будут множествами литералов, а a, b, g - термами, то есть константами, переменными или функциональными выражениями. В дополнении к обычному определению атомов и литералов будем записывать атомы равенства в виде a=b (терм a равен терму b). К таким термам можно применять подстановку.

Если для заданных предложений C1 и C2 = (a’ = b’, B) (или C2’ = (b’ = a’, B)), не имеющих общих переменных в общей части B выполняются условия:

1.   C1 содержит терм d.

2.   У d и a’ есть наиболее общий унификатор:

,

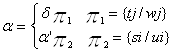где ui и wj – переменные соответственно из a’ и d,

то надо построить предложения =C1p1, а затем C#, заменяя a’ на b’p2 для какого-то одного вхождения a’ в C₁^*. Наконец вывести:

C3=(C#, Bp).

Формулировка весьма сложна, но ее реализация очень проста. В простейшем случае B пусто, так что предложения, содержащие высказывания с равенством, состоят из единственного атома выражающего равенство. Таким образом, из:

C1={Q(a)},

C2={a=b}

можно вывести:

C3={Q(b)}.

Несколько более сложный случай:

C1={Q(x)},

C2={(a=b)}.

Подстановка p = (a/x) дает:

C1^*={Q(a)},

C3={Q(b)}.

При одном применении парамодуляции подстановка a=bp2 применяется в С₁^* только один раз. Таким образом, если заданы предложения:

C1={Q(x), P(x)},

C2={(a=b)},

то одно применение парамодуляции с подстановкой p = (a/x) дает сначала

C₁^*={Q(a), P(a)},

а затем или

C3={Q(a),P(b)},

либо

C3={Q(b), P(a)}.

Для получения C4={Q(b), P(b)} требуется повторное применение парамодуляции.

Рассмотрим пример по сюжету известной сказки Андерсона «Принцесса на горошине», который может служить тестом на наличие королевской крови.

Определения для примера:

1.   x, y, z – переменные, принимающие значения на множестве людей.

2.   M(x): x – мужчина.

3.   C(x): x – простолюдин.

4.   D(x): x может почувствовать горошину через перину.

5.   x = k: x – король.

6.   x = q: x – королева.

7.   d(x,y): дочь x и y.

8.   x = p: x – принцесса.

Исходные предложения:

 - существует мужчина.

 - существует женщина.

 - любой мужчина не простолюдин король.

 - любая королева – женщина и не простолюдинка.

 - дочь короля и королевы – принцесса.

 - принцесса может почувствовать горошину.

Удалим квантор существования из предложений C1, C2, обозначив через f1, f2 сколемовские функции без переменных, так как перед квантором существования нет квантора общности.

 : f1 – мужчина.

 f2 – женщина.

Опускаем кванторы всеобщности в C3, C4. Проводим резолюцию C1 с C3, а затем C2 и C4. Получаем:

 f1 – король или простолюдин.

 f2 – королева или простолюдинка.

Затем осуществляем парамодуляцию C7 и C5. Это дает:

 дочь королевы и f1 – есть принцесса или f1 - простолюдин. Затем осуществляем парамодуляцию C8 и C9. Это дает:

 дочь f1 и f2 есть принцесса, либо f1, либо f2 – простолюдин. Наконец парамодуляция C10 с C6 дает:

 дочь f1 и f2 может почувствовать горошину, либо f1, либо f2 – простолюдин.

4.2.4 Стратегии очищения

Применение принципа резолюции без ограничений может привести к слишком большому количеству предложений, чтобы с ним можно было бы работать на практике. Поэтому надо уметь заранее определять, какие выполнять резолюции и какие производить выводы. На этом и основываются стратегии очищения.

Похожие работы

Общая терминология программирования

Скачать

71422

1

0

... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п.   Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...

Программирование и достижения компьютерной техники

Скачать

60551

0

0

... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники   1.         Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...

Графические возможности программирования в курсе информатики

Скачать

110612

10

19

... набор процедур и функций языков программирования Basic и Pascal, позволяют управлять графическим режимом работы экрана, создавать разнооборазные графические изображения и выводить на экран текстовые надписи. ГЛАВА 2. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ ЯЗЫКА ПРОГРАММИРОВАНИЯ В КУРСЕ ИНФОРМАТИКИ БАЗОВОЙ ШКОЛЫ (НА ПРИМЕРЕ BASIC И PASCAL)   2.1 Разработка мультимедиа курса «Графические возможности языков ...

Функциональное и логическое программирование

Скачать

11287

1

10

... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...