Навигация
В проверке содержит или не содержит S пустое предложение
1. В проверке содержит или не содержит S пустое предложение.
2. В проверке выводится или не выводится пустое предложение из S, если пустое предложение в S отсутствует.
Любое предложение Ci, из которого образуется S, является совокупностью атомарных предикатов или их отрицаний (предикат и его отрицание называются литералами), соединенных символами дизъюнкции, вида:
![]()
Сама же S является конъюнктивной формой, то есть имеет вид:
![]()
Следовательно, условием истинности S является условие истинности всех Ci в совокупности.
Условием ложности S является ложность по крайней мере одного Ci. Однако, условием, что Ci будет ложным в какой-нибудь интерпретации, является то, что множество ![]() будет пустым. Это легко показать. Положим, что это не так, тогда среди всех возможных интерпретаций имеется такая, что какой-нибудь из литералов этого множества или все они будут истиной и тогда Ci не будет ложью. Следовательно, если S содержит пустые предложения, формула (2) является ложью, а это показывает, что B выводится из группы предикатов A1, … , An, то есть из S.
будет пустым. Это легко показать. Положим, что это не так, тогда среди всех возможных интерпретаций имеется такая, что какой-нибудь из литералов этого множества или все они будут истиной и тогда Ci не будет ложью. Следовательно, если S содержит пустые предложения, формула (2) является ложью, а это показывает, что B выводится из группы предикатов A1, … , An, то есть из S.
4.2.3.1 Метод резолюций для логики высказываний
Предикат, который не содержит переменных, совпадает с высказыванием. Для упрощения рассмотрим сначала резолюцию для высказываний.
Предположим, что в множестве предложений есть дополнительные литералы (которые отличаются только символами отрицания L и ![]() ) вида:
) вида:

Исключим из этих двух предложений дополнительные литералы и представим оставшуюся часть в дизъюнктивной форме (такое представление называется резольвентой):
![]()
После проведения этой операции легко видеть, что C является логическим заключением Ci и Cj. Следовательно, добавление C к множеству S не влияет на вывод об истинности или ложности S. Если выполняется Ci = L, ![]() то C пусто. То что C является логическим заключением из S и C пусто, указывает на ложность исходной логической формулы.
то C пусто. То что C является логическим заключением из S и C пусто, указывает на ложность исходной логической формулы.
Приведем простой пример такого доказательства:

Получим доказательство принципом резолюции:

![]() - пустое предложение.
- пустое предложение.
Такой вывод теорем из аксиоматической системы носит название дедукции. Алгоритм дедуктивного вывода удобно представлять с помощью древовидной структуры:

Такая структура называется дедуктивным деревом или деревом вывода.
4.2.3.2 Принцип резолюции для логики предикатов
Поскольку в логике предикатов внутри предикатов содержатся переменные, то алгоритм доказательства несколько изменяется. В этом случае, перед тем как применить описанный алгоритм, будет проведена некоторая подстановка в переменные и вводится понятие унификации с помощью этой подстановки. Унификацию проиллюстрируем следующим простым примером.
Рассмотрим два предиката – L(x) и L(a). Предположим, что x – переменная, a - константа. В этих предикатах предикатные символы одинаковы, чего нельзя сказать о самих предикатах. Тем не менее подстановкой a в x одинаковыми (эта подстановка и называется унификацией).
Целью унификации является обеспечение возможности применения алгоритма доказательства для предикатов. Например, предположим имеем:

В данном случае L(x) и ![]() не находятся в дополнительном отношении. При подстановке a вместо x будут получены, соответственно,
не находятся в дополнительном отношении. При подстановке a вместо x будут получены, соответственно, ![]() и
и ![]() , и поскольку эти предикаты отличаются только символами отрицания, то они находятся в дополнительном отношении. Однако, операцию подстановки нельзя проводить при отсутствии каких-либо ограничений.
, и поскольку эти предикаты отличаются только символами отрицания, то они находятся в дополнительном отношении. Однако, операцию подстановки нельзя проводить при отсутствии каких-либо ограничений.
Подстановку t в x принято записывать как {t/x}. Поскольку в одной ППФ может находиться более одной переменной, можно оказаться необходимо провести более одной подстановки. Обычно эти подстановки записываются в виде упорядоченных пар {t1/x1, …, tn/xn}.
Условия, допускающие подстановку:
- xi – является переменной,
- ti – терм (константа, переменная, символ, функция) отличный от xi,
- для любой пары элементов из группы подстановок, например (ti/xi и tj/xj) в правых чачтях символов / не содержится одинаковых переменных.
Унификация
Обозначим группу подстановок {t1/x1, …, tn/xn} через q . Когда для некоторого представления L применяется подстановка содержащихся в ней переменных {x1, …, xn}, то результат подстановки, при которой переменные заменяются соответствующими им термами t1, …, tn принято обозначать Lq.
Если имеется группа различных выражений на основе предиката L, то есть L1, …, Lm}, то подстановка q, такая, что в результате все эти выражения становятся одинаковыми, то есть L1q = L2q = … = Lmq, q - называется унификатором {L1, …, Lm}. Если подобная подстановка q существует, то говорят, что множество {L1, …, Lm} унифицируемо.
Множества {L(x), L(a)} унифицируемо, при этом унификатором является подстановка (a/x).
Для одной группы выражений унификатор не обязательно единственный. Для группы выражений {L(x, y), L(z, f(x)} подстановка q = {x/z, f(x)/y} является унификатором, но является также унификатором и подстановка q = {a/x, a/z, f(a)/y}. Здесь a – константа, x – переменная. В таких случаях возникает проблема, какую подстановку лучше выбирать в качестве унификатора.
Операцию подстановки можно провести не за один раз, а разделив ее на несколько этапов. Ее можно разделить по группам переменных, проведя, например, подстановку {t1/x1, t2/x2, t3/x3, t4/x4} сначала для {t1/x1, t2/x2}, а затем для {t3/x3, t4/x4}. Допустимо также подстановку вида a/x разбить на две подстановки u/x и a/u. Результат последовательного выполнения двух подстановок q и l также подстановка и обозначается l°q.
Если существует несколько унификаторов, то среди них непременно найдется такая подстановка s, что все другие унификаторы являются подстановками, выражаемыми в виде s°l, как сложная форма, включающая эту подстановку. В результате подстановки переменные будут замещаться константами и описательная мощность ППФ будет ограничена.
Чтобы унифицировать два различных выражения предиката, необходима такая подстановка, при которой выражение с большей описательной мощностью согласуется с выражением с меньшей описательной мощностью. Такую подстановку принято называть «наиболее общим унификатором» (НОУ). Метод отыскания НОУ из заданной группы предикатов выражений называется алгоритмом унификации.
Этот алгоритм состоит в том, что сначала упорядочиваются выражения, которые подлежат унификации. Когда каждое выражение будет упорядочено в алфавитном порядке, среди них отыскивается такое, в котором соответствующие термы не совпадают межде собой.
Положим, что при просмотре последовательно всех выражений в порядке слева направо несовпадающими термами оказались x, t. Например, получено {L(a, t, f(z)), L(a, x, z)}. В этом случае, если:
1. x является переменной;
2. x не содержится в t, к группе подстановок добавляется {t/x}.
Если повторением этих операций будет обеспечено совпадение всех изначально заданных выражений, то они унифицируемы, а группа полученных подстановок является НОУ.
В приведенном примере третий терм в одном случае z, а в другом – f(z), первое условие выполняется, а второе – нарушается. Поэтому подстановка недопустима. Если в группе предикатных выражений остается хотя бы одно такое, для которого никакими подстановками нельзя получить совпадения с другими выражениями, такая группа называется неунифицируемой.
Рассмотрим другой пример:
P1 = L(a, x, f(g(y))),
P2 = L(z, f(z), f(u)).
1. Первые несовпадающие члены: {a, z}.
Подстановка: a/z. Имеем:
P1 = L(a, x, f(g(y))),
P2 = L(a, f(a), f(u)).
2. Первые несовпадающие элементы {x, f(a)}. Подстановка: [f(a)/x]. Имеем:
P1 = L(a, f(a), f(g(y))),
P2 = L(a, f(a), f(u)).
3. Первые несовпадающие элементы {g(y), u}. Подстановка: [g(y)/u]. Получаем совпадение. Следовательно, НОУ: [a/z, f(a)/x, g(y)/u].
Алгоритм доказательства
Пусть заданы:
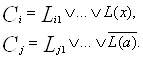
Предикаты ![]() делаются дополнительными с помощью подстановки [a/x]. Суждение о том, становятся ли два выражения дополнительными, выносится:
делаются дополнительными с помощью подстановки [a/x]. Суждение о том, становятся ли два выражения дополнительными, выносится:
Похожие работы
... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п. Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...
... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники 1. Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...
... набор процедур и функций языков программирования Basic и Pascal, позволяют управлять графическим режимом работы экрана, создавать разнооборазные графические изображения и выводить на экран текстовые надписи. ГЛАВА 2. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ ЯЗЫКА ПРОГРАММИРОВАНИЯ В КУРСЕ ИНФОРМАТИКИ БАЗОВОЙ ШКОЛЫ (НА ПРИМЕРЕ BASIC И PASCAL) 2.1 Разработка мультимедиа курса «Графические возможности языков ...
... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...
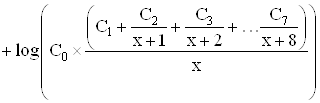
0 комментариев