Навигация
Варианта раскроя ДСП, 8 ч в смене; работа в 1 смену; 22 рабочих дня в месяц
3 варианта раскроя ДСП, 8 ч в смене; работа в 1 смену; 22 рабочих дня в месяц.
3. На складах хранится мука, которую необходимо завезти в хлебопекарни. Номера складов и номера хлебопекарен даны в таблице 1. Текущие тарифы перевозки муки [руб./т], ежемесячные запасы муки [т/мес] на складах и потребности хлебопекарен в муке [т/мес] указаны в табл. 2.
При этом необходимо учитывать, что из-за ремонтных работ временно нет возможности перевозить муку с некоторых складов в некоторые хлебопекарни. В табл. 1это показано в графе "Запрет перевозки" в формате № склада х № хлебопекарни. Например, «2x3» обозначает, что нельзя перевозить муку со склада № 2 в хлебопекарню № 3.
Кроме того, необходимо учесть, что некоторые хлебопекарни имеют договоры на гарантированную поставку муки с определенных складов. В табл. 1 это показано в графе "Гарантированная поставка" в формате № склада х № хлебопекарни = объем поставки. Например, «1x4=40» обозначает, что между складом № 1 и магазином № 4 заключен договор на обязательную поставку 40 т муки.
Необходимо организовать поставки наилучшим образом, учитывая, что мука хранится и транспортируется в мешках весом по 50 кг.
Таблица 1
Номер склада, хлебопекарни, запрещенные или гарантированные поставки
| № Варианта | № Складов | № Хлебопекарен | Запрет перевозки | Гарантированная поставка, т/мес. |
| 4 | 1,2, 3,4 | 3, 4, 5 | 3x3, 4x5 | 3x5=40 |
Таблица 2
Запасы, потребности и тарифы перевозок
| Склады | Хлебопекарни | |||||
| 1 | 2 | 3 | 4 | 5 | Запас, т/мес. | |
| 1 | 400 | 600 | 800 | 200 | 200 | 80 |
| 2 | 300 | 100 | 500 | 600 | 500 | 70 |
| 3 | 500 | 200 | 100 | 600 | 300 | 60 |
| 4 | 300 | 700 | 200 | 400 | 900 | 55 |
| 5 | 200 | 500 | 800 | 200 | 400 | 65 |
| Спрос, т/мес. | 77,86 | 56,78 | 58.88 | 62,44 | 73,92 | |
2. Теоретическая основа линейного программирования
2.1.Постановка задачи
Постановка практической задачи ЛП включает следующие основные этапы:
· определение показателя эффективности, переменных задачи,
· задание линейной целевой функции S(x), подлежащей минимизации или максимизации,
· задание ограничений.
Приведем сейчас общую математическую формулировку основной задачи линейного программирования.
Дана система линейных уравнений с n неизвестными:
a11 x1 + a11 x2 + …… + a11 xn ![]() =
=![]() b1 ,
b1 ,
a21 x1 + a22 x2 + …… + a2n xn ![]() =
=![]() b2 ,
b2 ,
am1 x1 + am2 x2 + …… + amn xn ![]() =
=![]() bm ,
bm ,
и линейная функция
f = c1 x1 + c2 x2 +………+ cn xn (1.2)
Требуется найти такое неотрицательное решение системы
x1 ≥0, x2 ≥0, … … , xn ≥0 (1.3)
при котором функция f принимает наименьшее значение.
Уравнения (1.1) называют системой ограничений данной задачи; функцию f — целевой функцией (или линейной формой).
2.2.Методы решения задач линейного программирования
Похожие работы
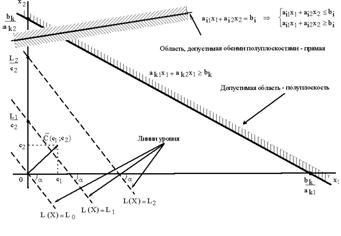
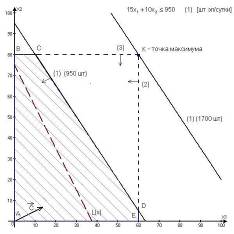
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
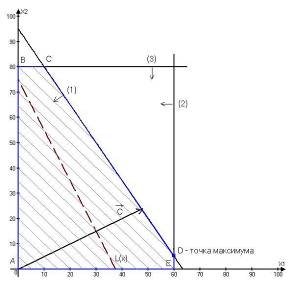
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...





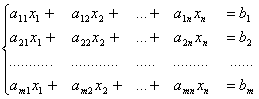
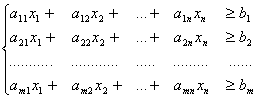
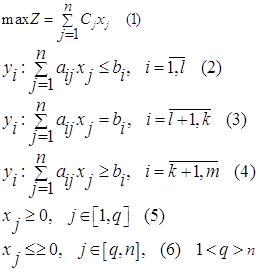
0 комментариев