Навигация
Щелчком на ярлычке Отчет по устойчивости откроем содержимое отчета на рабочем листе (рис. 8)
34424
знака
6
таблиц
3
изображения
2. Щелчком на ярлычке Отчет по устойчивости откроем содержимое отчета на рабочем листе (рис. 8).
Отчет по устойчивости содержит две таблицы.
В первой таблице (Изменяемые ячейки) приводятся следующие значения переменных:
· результаты решения задачи (графа «Результ. значение»);
· нормированная стоимость, т.е. дополнительные двойственные переменные vj, 
, которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;
· коэффициенты целевой функции (графа «Целевой коэффициент»);
· предельные значения приращения коэффициентов Dcj целевой функции (последние две графы), при которых сохраняется набор переменных, входящих в оптимальное решение.
Во второй таблице приводятся значения ограничений:
· значения используемых (графа «Результ. Значение») и заданных (графа «Ограничение, правая часть») ресурсов;
· теневая цена, т. е. двойственные оценки zi, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
· значения приращения ресурсов Δbi (последние две графы), при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
3. Отчёт по переделам (рис.9) показывает, в каких пределах может меняться выпуск продукции, вошедшей в оптимальное решение, при сохранении его структуры:
· приводятся значения хi в оптимальном решении (графа «Значение»);
· даются нижние и верхние пределы изменения хi и соответствующие значения целевой функции (в графах «Целевой результат»).
3.2. Решение одноиндексной задачи линейного программирования
3.2.1. Построение модели
В данной задаче искомыми неизвестными являются количество полок каждого вида, которые будут произведены в текущем месяце. Таким образом, Х1 – количество полок А(шт./мес.); Х2 – количество полок В1(шт./мес.); Х3 – количество полок В2(шт./мес.).
Целевая функция: Прибыль определяется разностью между ценой и себестоимостью, тогда:
L(х) = (192-150)х1+(154-120)х2+(147-134)х3 мах
Руб./шт.* шт./мес. =руб./мес.
Ограничения:
· Ограничения по фонду времени ( с использованием трудоемкости работ)
3,2 х1
27*8*1*22
ч/шт.* шт./мес. чел.* ч/(чел.см.)*см./дн. * дн./мес.
ч/мес. ч/мес.
3,2 ч/шт. (Тр1) – это время, затрачиваемое на столярные работы при производстве одной полки типа А;
27 чел. (Р1) – это количество столяров;
8ч/(чел.*см) – количество часов работы 1 человека в течении смены;
1см./дн. – количество смен в одном рабочем дне;
22 дн./мес. – количество рабочих дней в месяце
Необходимо произвести проверку единиц измерения!
Аналогично – упаковочные работы:
6/60х1+9/60х2+10/60х3 7,4*8*1*22
ч/мес. ч/мес
7 чел. (Р2) – это количество упаковщиков
Ограничение по фонду времени на покрытие лаком полок типа А:
1/2*х1 7,4*1*22
ч/шт.*шт./мес. ч/см.*см./дн.*дн./мес.
ч/мес. ч/мес.
1/2 – коэффициент, показывающий количество часов, приходящихся на покрытие лаком одной полки типа А.
Автомат работает в смену 7,4 ч в смену (ФВ1).
Ограничение по фонду времени на резку стекла для полок типа А и В2:
2/180х1+2/180х3
7,1*1*22
ч/шт.*шт./мес. ч/см.*см./дн.*дн./мес.
ч/мес. ч/мес.
Ограничения по фонду времени на производство комплектующих полок типа В1 и В2:
1/7х2+1/7х37,8*1*22
ч/шт.*шт./мес. ч/см.*см./дн.*дн./мес.
ч/мес. ч/мес.
· Ограничения по запасу расходуемых в производстве материалов (по запасу используемых для производства полок деталей)..
Целесообразно ориентироваться не на количество листов ДСП, а на количество комплектов для полок, которые можно получить из имеющегося запаса ДСП. Поскольку листы ДСП можно раскраивает различными способами и получать при этом различное количество деталей и комплектов, то обозначим месячный запас комплектов в правой части как Yкомпл и рассмотрим способ его численного определения позже.
1х2+1х3 Yкомпл
Компл./шт.*шт./мес. Компл./мес.
Компл./мес. Компл./мес.
Аналогично составляем ограничения по запасу задних стенок из ДВП для полок В1, В2:
1х2+1х3215*6
Задняя стенка/шт.*шт./мес. лист ДВП/мес.*задняя стенка/лист ДВП
Задняя стенка/мес. Задняя стенка/мес.
Где 215 – ежемесячный запас листов ДВП
6 – количество задних стенок полок из каждого листа ДВП.
Ограничения по запасу стекол для полок А и В2:
2х1+2х3240*13
стекло/шт.*шт./мес. лист стекла /мес.*стекло /лист стекла
стекло/мес. стекло/мес.
Где 240 – ежемесячный запас стекол
13 – количество стекол из каждого листа стекла.
· Ограничения по емкости вспомогательных помещений и рынка.
Ограничение по количеству полок А, которые может вместить сушилка:
х1 55*22
шт./мес. шт./дн.*дн./мес.
шт./мес. шт./мес.
где 55 – количество полок, которые могут быть просушены в течение месяца.
Ограничение на количество полок всех видов, которые может вместить склад готовой продукции:
х1+х2+х3370-80+72*22
шт./мес. шт./мес.-шт./мес.+шт./дн.*дн./мес.
шт./мес. шт./мес.
Здесь учитывается, что общая емкость склада уменьшается на остаток полок, которые остались невывезенными с прошлого месяца. Кроме того, в течение месяца каждый день будет освобождаться по N мест для полок.
Ограничение по примерной емкости рынка:
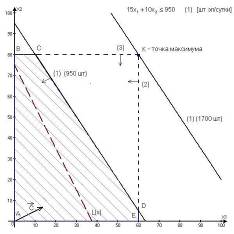
х1+х2+х31100
шт./мес. шт./мес.
1100 – емкость рынка по всем видам полок.
· Ограничение по гарантированному заказу.
х1
5,
х3
12
шт./мес. шт./мес.
Необходимо произвести как минимум 5 полок А и 12 полок В3.
· Ограничения по соотношению объемов продаж различных товаров.
Процентное отношение количество полок А и В1 ко всему объему продаж:
(х1-5)+х20,43[(х1-5)+х2+(х3-12)]
0,57х1+0,57х2-0,43х3 - 2,31
Шт./мес. шт./мес.
· Определение количества комплектов для полок В1 и В2
Похожие работы
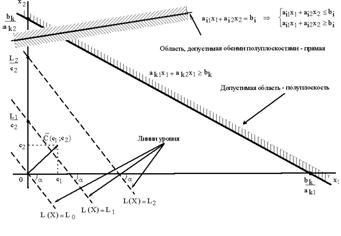
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
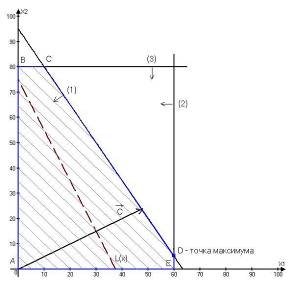
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
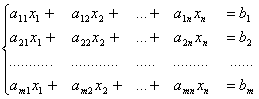
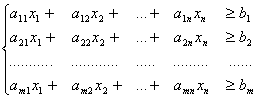
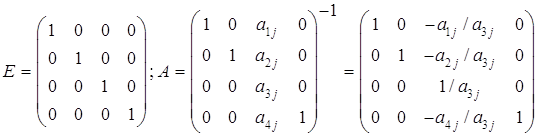
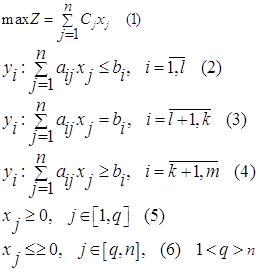
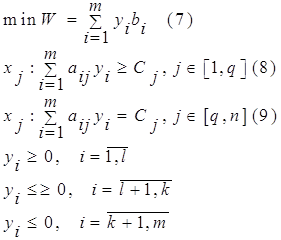
0 комментариев