Навигация
Первый этап решения задачи
34424
знака
6
таблиц
3
изображения
3.2.2. Первый этап решения задачи
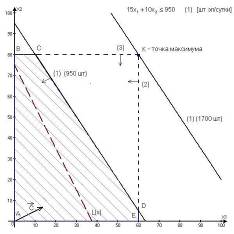
В зависимости от размеров листов ДСП и габаритов полок детали В1 и В2 можно выкроить различными способами. Рассмотрим 3 возможных варианта такого раскроя (рис.10).
L(Y)=Yкомпл мах комппл./мес.
Согласно 1 варианту из одного листа ДСП для полок В1 и В2 можно выкроить 19 деталей верхней и нижней стенок, а также 9 деталей боковых стенок. По 2 варианту раскроя получаем 12 деталей верхней и нижней стенок и 36 деталей боковых стенок. По 3 варианту раскроя получаем 16 деталей верхней или нижней стенок и 18 деталей боковых стенок.
Обозначим количество листов ДСП, раскроенных в течение месяца : по 1-му варранту через у1(лист./мес.); по 2 варианту – у2(лист./мес.); по 3 варианту – у3(лист./мес.). Таким образом, наша цель – укомплектовка максимального количества полок – описывается целевой функцией:
L(Y)=Yкомпл мах
Количество всех раскроенных листов ДСП не должно превышать 415, то есть ежемесячный запас их на складе:
у1+у2+у3
415
лист./мес.
Количество верхних и нижних стенок, получаемых при раскрои:
19у1+12у2+16у3
2Yкомпл
дет,мес. дет./мес.
Ограничение, задающие нижнюю границу количества боковых стенок полок:
9у1+36у2+18у3 2Yкомпл
дет,мес. дет./мес.
Получаем модель задачи, позволяющую раскроить максимальное количество комплектов:
L(Y)=Yкомпл мах
у1+у2+у3 415
19у1+12у2+16у3 2Yкомпл
9у1+36у2+18у3 2Yкомпл
у1,у2,у3,Yкомпл0
Решим данную задачу с помощью функции Поиск решения в MS Excel. Для этого повторим все пункты выполнения работы 3.1.2 – 3.1.3 (рис.11).
3.2.3. Решение исходной одноиндексной задачи
Решив задачу для варианта 0 мы получил значение правой части ограничения Y = 3515 комплектов, после чего решаем исходную задачу, модель которой имеет следующий вид:
L(х) = 42х1+34х2+13х3 мах
3,2х1
4752;
0,1х1+0,15х2+0,167х31232;
0,5х1162,8;
0,011х1+0,011х3156,2;
0,143х2+0,143х3171,6;
х2+х33515;
х2+х31290;
2х1+2х33120;
х11210;
х1+х2+х31874;
х1+х2+х31100;
х15;
х312;
0,57х1+0.57х2+0,43х3-2,31;
х1,х2,х30
Решим задачу с использованием функции Поиск решения в MS Excel аналогично пунктам 3.1.2-3.1.3.
В ячейку Е5 введем целевую функцию, в ячейки В6:В19 – ограничения, переменные будем изменять в ячейках В3:В5 (рис.12).
Решив задачу, получаем:
х1=326шт./мес., х2=762 шт./мес., х3 = 12 шт./мес.,
L(X) = 39753 руб./мес.,
т.е. в текущем месяце необходимо произвести 326 полок А, 762 полки В1, 12 полок В2. После реализации всех произведенных полок комбинат получит прибыль в размере 39753 рублей. Оформим отчеты аналогично п.3.1.4.
Отчет по результатам, состоящий из 3 таблиц:
1. Информация о целевой функции.
2. Информация о значениях переменных, полученных в результате решения задачи.
3. Результаты оптимального решения для ограничений и для граничных условий.
Анализ отчета показывает, что мы можем уменьшить фонд времени фонд времени по производству полок В на 60,86 ч и это никак не повлияет на оптимальное решение. Таким образом, мы снизим время работы автомата, производящего комплектующие полки В1 и В2.
Емкость сушилки может быть снижена до 326 полок.
На основании проведенного анализа можно сделать вывод о том, что существуют причины, не позволяющие мебельному комбинату выпускать большее количество полок и получать большую прибыль. Проанализировать эти причины позволяет отчет по устойчивости.
Отчет по устойчивости
Проанализировав 2 таблицу, мы увидим, что целесообразно увеличить емкость рынка самое большое на 425,6 = 426 полок. Это приведет к новым оптимальным решениям, увеличивающим прибыль по сравнению с найденной. Дальнейшее увеличение емкости рынка сверх указанных пределов не будет больше улучшать решение. Из колонки «Теневая цена» видно, что каждая полка, которая будет размещена на рынке, принесет прибыль равную 34 руб..
Отчет по пределам показывает найденные результаты и пределы, в которых они могут изменяться.
3.3. Решение двухиндексной задачи линейного программирования. Транспортная задача
3.3.1. Определение переменных
Обозначим через хij [меш.] количество мешков с мукой, которые будут перевезены с i-го склада в j-ю хлебопекарню.
3.3.2. Проверка сбалансированности задачи
Прежде чем проверять сбалансированность задачи, надо исключить объем гарантированной поставки из дальнейшего рассмотрения. Для этого вычтем 40 т из следующих величин:
· из запаса третьего склада = 60-40= 20т/мес.;
· из потребности в муке пятой хлебопекарни
b2 = 73,92-40 = 33,92 т/мес.
Согласно условию задачи мука хранится и перевозится в мешках по 50 кг, то есть единицами измерения переменных хij являются мешки муки. Но
запасы муки на складах и потребности в ней магазинов заданы в тоннах. Поэтому для проверки баланса и дальнейшего решения задачи приведем эти величины к одной единице измерения - мешкам. Например, запас муки на
первом складе равен 80 т-мес., или 80т/мес. / 0,050т./меш.= 1600 меш/мес, а потребность третьей хлебопекарни составляет 58,88т/мес, или 58,88т/мес / 0,050 т./меш.= 1178меш./мес. Округление при расчете потребностей надо проводить в большую сторону, иначе потребность в муке не будет удовлетворена полностью.
Для данной ТЗ имеет место соотношение
склады хлебопекарни
1600+1400+400+1100 < 1178+1249+679
4500меш./мес. 3106 меш./мес.
Ежемесячный суммарный запас муки на складах больше суммарной потребности хлебопекарен на 1394 мешков муки, откуда следует вывод: ТЗ не сбалансирована.
Похожие работы
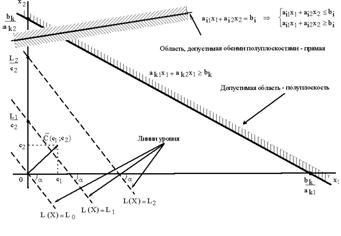
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
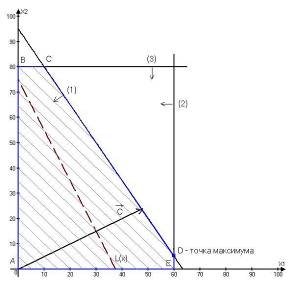
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
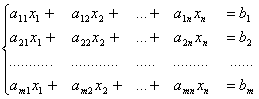
0 комментариев