Идентификация объекта управления по временным трендам

3.  Идентификация объекта управления по временным трендам

 

3.1 Основные понятия теории идентификации

Идентификация (отождествление) в технике связана с процессом построения модели исследуемого объекта. В дальнейшем под идентификацией понимается процесс построения математической модели технического устройства (объекта) по его измеряемым входным и выходным сигналам. При этом под объектом можно понимать любые материальные (физические процессы, технические объекты) и нематериальные (знаковые) элементы и системы Класс рассматриваемых моделей охватывает статические и динамические модели, описываемые соответственно алгебраическими и обыкновенными дифференциальными уравнениями.

С развитием и широким распространением быстродействующих вычислительных машин и аппаратуры дистанционного измерения и передачи данных (телеметрической аппаратуры) наметилась тенденция к полной автоматизации процессов построения математических моделей объектов и созданию адаптивных систем управления, самонастраивающихся микропроцессорных регуляторов для различных технических систем. Так, для идентификации широко привлекаются известные в статистике методы наименьших квадратов, максимального правдоподобия, стохастической аппроксимации и их разновидности [2, 3, 9, 23, 30, 32, 33, 73, 82, 99, 100].

Построение математической модели достаточно сложного объекта представляет собой довольно трудоемкий процесс, включающий этапы выбора вида и структуры модели идентифицируемого объекта, выбора или разработки метода и численных алгоритмов идентификации с учетом возможностей телеметрической аппаратуры и вычислительных средств, предварительной (первичной) обработки результатов телеизмерений, получения оценок характеристик модели, анализа этих оценок и проверки степени идентичности (адекватности) модели и реального объекта. Задача каждого из указанных этапов составляет весьма сложную проблему. Решение ее немыслимо без глубокого знания соответствующих дисциплин и теории. В целом же инженеру, работающему в области идентификации технических объектов, необходимо достаточно свободно ориентироваться в теории вероятностей, современной математической статистике и вычислительной математике, а также иметь представление о теории моделирования, теории управления и принципах построения и функционирования идентифицируемых объектов.

В настоящее время проблемы, связанные с созданием математических моделей объектов технологических процессов, экономики и живой природы, формируют одно из основных направлений науки и техники – моделирование. Это объясняется тем, что математические модели объектов широко применяются как при создании систем управления этими объектами, так и при их эксплуатации.

Объекты и системы представляют собой совокупность материальных тел, находящихся в непрерывном взаимодействии друг c другом и с окружающей средой. Построение математической модели объекта может производиться несколькими методами: аналитическим, экспериментальным и экспериментально-аналитическим [49, 57, 73, 100].

Аналитический метод предусматривает получение математического описания объекта на основе законов физики, механики, химии и т. д. Такой подход дает положительный результат, если рассматриваемый объект достаточно прост по структуре и хорошо изучен. Если же объект изучен недостаточно или же настолько сложен, что аналитическое описание его математической моделью практически невозможно, прибегают к экспериментальным методам, суть которых сводится к статистической обработке технологических данных. При экспериментально-аналитическом методе априорная модель, полученная аналитическим путем, уточняется в соответствующих экспериментах.

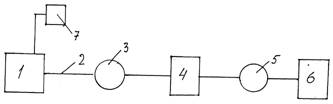
Взаимодействие объекта с окружающей средой поясним с помощью простейшей схемы (рис. 3.1). Воздействия внешней среды на объект в обобщенном виде изображены стрелками, направленными к объекту и обозначенными через x и v. Объект, в свою очередь, воздействует на окружающую среду. Это воздействие показано стрелкой, направленной от объекта и обозначенной через y. Величину y принято называть выходным воздействием или выходной величиной объекта.

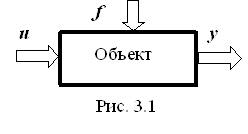
Рассмотрим более подробно воздействие среды на объект. Совокупность таких воздействий окружающего мира на объект можно разделить на две группы в соответствии с характером влияния среды на переменные состояния (фазовые координаты) объекта. В первую группу входят те воздействия, которые в точке приложения изменяют переменные состояния аддитивно. Это означает, что сигналы, пропорциональные этим воздействиям, суммируются с сигналами, пропорциональными соответствующим переменным состояния.

Эти воздействия называют «входными», или «внешними», воздействиями. В дальнейшем будем называть эти воздействия «входными». Входные воздействия могут быть полезными (управляющими сигналами u) и помехами (возмущающими воздействиями f).

Вторая группа воздействий внешней среды изменяет переменные состояния объекта косвенно, обычно не аддитивно. Эти воздействия приводят к изменению оператора объекта (системы) А, под которым понимают закон преобразования входных воздействий в выходные переменные объекта. Вторую группу воздействий будем называть операторной, а воздействия – операторными.

Так, например, повышение температуры электродвигателя приводит к падению мощности и даже выходу его из строя.

В общем случае входные и выходные воздействия могут описываться определенными функциями (обычно функциями времени). Математически соответствие между входной и выходной функциями можно записать в виде выражения

(3.1)

где A(f) – оператор, зависящий от возмущений (операторных воздействий);  – вектор выходных координат объекта;  – вектор управления (входа).

Оператор объекта является его математической характеристикой, т. е. математической моделью объекта.

Примерами операторов могут быть:

– оператор дифференцирования p:

;  (3.2)

– дифференциальный оператор D(y) :

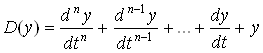, (3.3)

– оператор обыкновенного линейного дифференциального уравнения n-го порядка L(y)

 

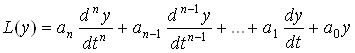 , (3.4)

– линейный интегральный оператор

, (3.5)

где  – функция веса объекта;

Математически операторы определяются в соответствующих пространствах, т. е. на множествах элементов, над которыми совершаются преобразования. Примерами таких пространств являются пространства: непрерывных функций; непрерывных функций, имеющих непрерывные производные до n-го порядка (n > 0); функций с суммируемым квадратом и т. д. Множества входных и выходных сигналов объектов и систем могут рассматриваться как те или иные метрические пространства [4,12, 13, 37, 44].

Формально оператор характеризуется структурой и параметрами. Так, структура дифференциального оператора (1.3) определяется его порядком n. Для оператора дифференциального уравнения (1.4) структура задается его порядком n, а параметрами служат величины ai(t), [i = 0, n]. Таким образом, задачу идентификации в общем виде можно ставить как задачу определения оператора объекта, преобразующего входные воздействия в выходные.