Структурированные модели

4.2 Структурированные модели

Реальные объекты управления представляют собой совокупность отдельных элементов и блоков соединенных между собой посредством связей. Поэтому в практике гораздо удобнее бывает представлять математическую модель всей системы, как совокупность относительно простых математических моделей отдельных элементов и блоков объекта, т.е. структурированную модель. Такая форма математического описания в отличии от (4.6) отражает не только физические, но и технические принципы построения системы управления и позволяет исследовать процессы происходящие не только в системе в целом, но и процессы в отдельных ее элементах.

Структурированные модели, учитывающие техническую организацию систем управления, создаются на основе следующих допущений:

1. Все элементы системы являются простейшими звеньями, т.е. имеют один вход и один выход. Если звено характеризуется несколькими обобщенными координатами, то в качестве выходной величины выбирается та координата, которая является выходной или регулируемой величиной звена.

2. Все звенья, из которых состоит система, является детектирующими. В детектирующем звене выходная величина зависит только от входной. Если выходная величина звена оказывает влияние на входную, то звено называется недетектирующим.

Допущения о том, что в состав системы управления должны входить только детектирующие звенья не сужает область применения структурированных моделей, так как недетектирующее звено может рассматривать как совокупность детектирующих звеньев охватываемых обратной связью.

Таким образом, структурированная модель системы управления разбивается на ряд взаимосвязанных математических моделей отдельных звеньев. Тогда, последовательно, исключая из рассмотрения все внутренние переменные, являющиеся входными или выходными сигналами внутренних звеньев, можно найти дифференциальное уравнение описывающее взаимосвязь входной и выходной величины системы в виде.

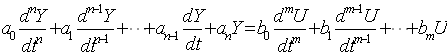, (4.8)

где - постоянные коэффициенты;

n - порядок системы.

Для реальных физически реализуемых систем управления m < n .

Подвергая (4.8) преобразованию Лапласа при нулевых начальных условиях получим алгебраическое уравнение, связывающее изображения по Лапласу от входной X(p) и выходной Y(p) величины объекта

, (4.9)

где p – оператор Лапласа

Последнее уравнение можно представить в виде:

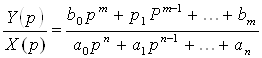. (4.10)

Это отношение называется передаточной функцией объекта и обозначается символом W(p).

Передаточной функцией системы называется отношение выходной величины к входной, преобразованных по Лапласу при нулевых начальных условиях и возмущениях. Зная передаточную функцию системы или звена можно легко получить дифференциальное уравнение в форме (4.8), справедливо также и обратное утверждение.

Введение векторных переменных при рассмотрении многомерных объектов позволяет для линейных систем использовать привычный аппарат передаточных функций и структурных схем, однако понятие передаточной функции значительно расширяется.

Пусть имеется многомерный объект управления со структурной схемой рис. 4.1 б. По аналогии с одномерными системами (4.9) можно записать:

, (4.11)

где Q(p)-квадратная матрица операторных коэффициентов размера

,

R(p)- прямоугольная матрица операторных коэффициентов размера

,

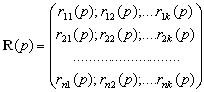S(p)- прямоугольная матрица операторных коэффициентов размера

.

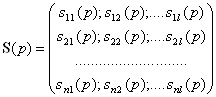Для получения системы дифференциальных уравнений необходимо перемножить прямоугольную или квадратную матрицы на матрицы - столбцы соответствующих переменных объекта. Взаимосвязь уравнений состояния (4.6) с уравнениями системы в виде (4.11) определяется из следующих соотношений. Из второго уравнения (4.6) выразим переменную  через

 (4.12)

и подставим это выражение в первое уравнение (4.6)

. (4.13)

Преобразовывая по Лапласу (4.13) и группируя подобные члены, получим выражение аналогичное (4.11).

, (4.14)

где  - единичная матрица.

Полагая , а  найдем взаимосвязь параметров структурированной модели и модели в пространстве состояний

, , . (4.15)

По аналогии с одномерными системами, используя основные правила теории матриц, можно ввести понятие матрицы передаточной функции.

Если умножить (4.14) на обратную матрицу , то получим:

 (4.16)

Отсюда можно получить выражение для матриц передаточных функций системы по управлению

 (4.17)

и возмущению

 (4.18)

Как для одномерных, так и для многомерных систем одной и той же матрице передаточной функции может соответствовать несколько вариантов структурных схем и уравнений состояния. Т.е. по уравнениям состояния матрица передаточной функции может быть получена однозначно, обратное утверждение будет неверным. Это связано с тем, что при получении выражения передаточной функции исключаются из рассмотрения все внутренние переменные структурированной модели, которые нельзя уже восстановить по выражению передаточной функции.

Похожие работы

Орская ТЭЦ

Скачать

143711

9

3

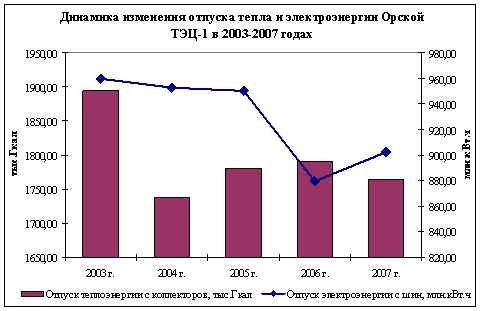
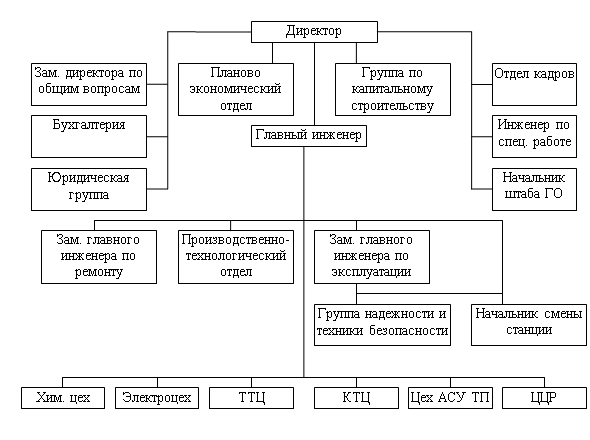
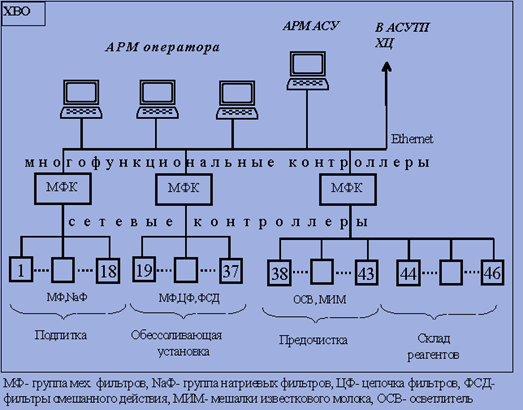
... функционирующий элемент технологического оборудования: механический фильтр, осветлитель, цепочку фильтров блока обессоливания, группу баков и насосов и т.п.   3. Технологическая схема приготовления топлива В котлах Орской ТЭЦ-1 сжигается природный газ, представляющий собой механические смеси различных газов.Состав газа ( в %)а) метан - 97,37б) ...

Квалификационная работа для сотрудников Газпрома

Скачать

10865

1

0

... VS 24 ат.д.о и после задвижки, медленно открыть ее полностью, также медленно полностью открыть отсечную задвижку VB после турбины. 1.14. Параллельно с началом прогрева турбины включить в работу конденсаторы осевшего пара для чего: - прогреть п/провод до эжектора; - включить по воде конденсатор осевшего пара; - включить в работу эжектор и создать давление в линии отсоса пара уплотнений 0,3 ...

Разработка ресурсосберегающих технологий и режимов на городском электрическом транспорте

Скачать

241230

29

12

... состава, введенным согласно закону «О городском пассажирском транспорте», договорных отношений между местными властями и транспортными предприятиями. 3. РЕСУРСОСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ НА ГОРОДСКОМ ЭЛЕКТРИЧЕСКОМ ТРАНСПОРТЕ 3.1. Регенерация масел Установки для регенерации отработанных масел и схемы технологического процесса Проводимые исследования кафедрой городского электрического транспорта ( ...

Система питания двигателей автобусов ПАЗ

Скачать

44550

2

13

... , что в условиях повышенных требований к защите окружающей среды и расходу топлива дизели остаются наиболее перспективными двигателями. В настоящее время в ФРГ на 14 % автомобилей установлены дизели, во Франции — на каждом третьем автомобиле, а в Австрии — на каждом втором.   2. Система питания автомобиля ПАЗ 4230   2.1 Описание конструкции, принципа работы системы и основных элементов.   ...