Навигация
Нелинейные или позиционные регуляторы
2. Нелинейные или позиционные регуляторы.
К ним относятся:
- двухпозиционные регуляторы, у которых регулирующая величина принимает два фиксированных значения «включено – выключено»;
- трехпозиционные регуляторы, у которых регулирующая величина принимает три фиксированных значения «включено - выключено –реверс»;
Наиболее широко распространенным является ПИД-регулятор, реализующий закон регулирования в функции от ошибки регулирования е.
![]() , (5.4)
, (5.4)
или в операторной форме
![]() , (5.5)
, (5.5)
где Wp (p) передаточная функция регулятора равная
![]() . (5.6)
. (5.6)
Иногда используют модифицированный закон регулирования, которому соответствует следующее выражение передаточной функции
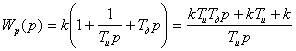 . (5.7)
. (5.7)
Для фильтрации высокочастотных помех возникающих в цепях управления в ПИД-регулятор дополнительно включается низкочастотный фильтр. В этом случае передаточная функция регулятора будет выглядеть
![]() . (5.8)
. (5.8)
ПИД-регулятор позволяет реализовать более простые законы регулирования путем исключения той или иной составляющей из закона регулирования. Дополнительно кроме ПИД-регулятора используются П - регулятор, И - регулятор ПИ - регулятор.
Широкое распространение таких регуляторов обусловлено простой схемной или программной реализацией закона регулирования, невысокой чувствительностью параметров настройки регулятора к изменению параметров объекта (грубостью или робастностью), сравнительно простой настройкой регулятора под конкретный объект. Недостатком этих регуляторов является не очень высокое качество регулирования особенно для сложных объектов имеющих в своем составе нелинейные элементы и звенья запаздывания. Более высокое качество регулирования обеспечивают регуляторы состояния, у которых закон управления представляет собой линейную функцию от переменных состояния объекта
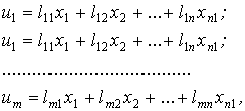 (5.9)
(5.9)
В матричном виде эти уравнения запишутся
![]() . (5.10)
. (5.10)
В том случае если не все компоненты вектора состояния x доступны измерению, используют специальные устройства (наблюдатели состояния), позволяющие восстановить вектор состояния x по измеренному вектору регулируемых величин y.
Если замыкать обратную связь по регулируемым величинам то закон управления (5.9) преобразуется к виду аналогичному (5.5):
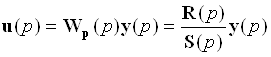 . (5.11)
. (5.11)
где Wp(p) – матричная передаточная функция регулятора состояния отличная от передаточной функции ПИД-регулятора.
В отличие от ПИД-регулятора регулятор состояния применим для многомерных объектов и обеспечивает лучшее качество регулирования. Однако он сложен в настройке и не обладает свойством грубости (робастности).
Для объектов не требующих высокой точности регулирования можно использовать регуляторы по возмущению. Структурная схема подключения такого регулятора к объекту приведена на рис. 5.1.

Рис. 5.1. Структурная схема системы с регулятором по возмущению.
Если известны передаточные функции объекта по правлению Wu(p) и возмущению Wf(p), то передаточная функция регулятора Wp(p) находится из условия полной компенсации возмущения.
![]() . (5.12)
. (5.12)
Откуда 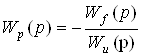 . (5.13)
. (5.13)
Недостатком регуляторов по возмущению является низкая точность регулирования, так как такой регулятор компенсирует действие на объект только контролируемых возмущений.
Достоинства обеих принципов регулирования по отклонению (ошибке) и возмущению совмещаются в комбинированных регуляторах. Рассмотрим структурную схему системы с комбинированным регулятором, компенсирующим динамическую ошибку системы, возникающую от изменения задания
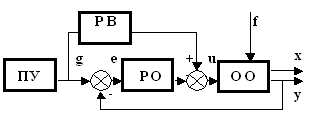
Рис. 5.2. Структурная схема системы с комбинированным регулятором.
Найдем передаточную функцию Wg(p) регулятора по возмущению РВ, обеспечивающую компенсацию задания g в системе условия. Для этого запишем передаточную функцию замкнутой системы по ошибке
![]() . (5.14)
. (5.14)
Откуда следует, что ошибка будет равна нулю, если We(p)=0, тогда
 . (5.15)
. (5.15)
Позиционные регуляторы, реализующие нелинейные законы регулирования имеют статическую характеристику релейного элемента (рис. 5.3).

Рис. 5.3. Статическая характеристика позиционного регулятора.
Изменяя настройки позиционного регулятора можно получать различные законы регулирования:
- двухпозиционный закон регулирования, имеющий статическую характеристику идеального реле:
- двухпозиционный закон регулирования, имеющий статическую характеристику идеального реле с гистерезисом;
- трехпозиционный закон регулирования, имеющий статическую характеристику идеального реле: с зоной нечувствительности;
- трехпозиционный закон регулирования, имеющий статическую характеристику идеального реле: с зоной нечувствительности и гистерезисом;
Достоинством позиционных регуляторов является простота конструкции и настройки, высокое быстродействие. К недостаткам относятся невысокая точность регулирования и возможность возникновения в системе режима автоколебаний.
Проведем расчет настроек ПИД –регулятора для системы заданной структурной схемой рис. 5.4.
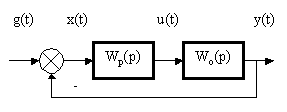
Рис. 5.4.
Передаточные функции регулятора Wp(p) и объекта Wo(p) имеют следующие выражения ; (5.16)
; (5.16)
 . (5.17)
. (5.17)
Если выбрать параметры настройки регулятора из условия равенства числителя передаточной функции регулятора знаменателю передаточной функции объекта
![]() , (5.18)
, (5.18)
то передаточные функции разомкнутой W(p) и замкнутой Wз(p) системы примут вид
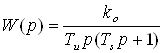 ; (5.19)
; (5.19)
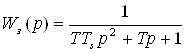 , (5.20)
, (5.20)
где постоянная времени замкнутой системы 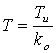 .
.
Характер переходных процессов в системе будет определяться корнями характеристического уравнения, которые в свою очередь зависят от его дискриминанта D
 (5.21)
(5.21)
Проведем настройку регулятора на границе апериодического и колебательного процесса, которая достигается при D=0. Откуда следует, что
![]() (5.22)
(5.22)
Из условия (5.18) вытекают следующие уравнения, связывающие параметры объекта и регулятора
![]() (5.23)
(5.23)
![]() (5.24)
(5.24)
Для разрешимости системы уравнений (5.22) – (5.23) дополним их условием предельно допустимого значения управления Umax при подаче на вход единичной ступенчатой функции. Значение управления на выходе регулятора найдем из условий теоремы о предельном значении передаточной функции
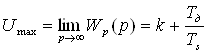 (5.25)
(5.25)
Решая систему уравнений (5.22) - (5.25) найдем неизвестные параметры настройки регулятора
 (5.26)
(5.26)
Ниже приведен расчет настроек регулятора и показателей качества системы регулирования.
Параметры регулятора
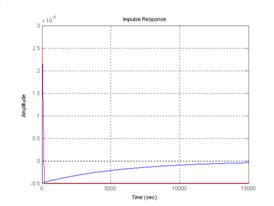
Рис. 5.5. Функция веса объекта и системы с ПИД – регулятором
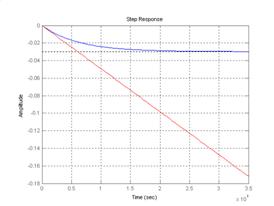
Рис. 5.6. Переходная характеристика объекта и системы с ПИД – регулятором.
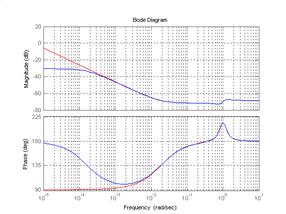
Рис. 5.7. ЛАЧХ и ФЧХ объекта и разомкнутой системы с ПИД – регулятором.
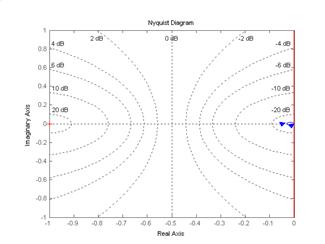
Рис. 5.8. АФЧХ объекта и системы с ПИД – регулятором.
6. Разработка структурной схемы системы
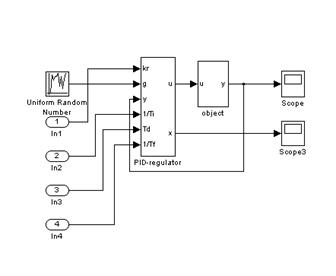
Рис. 6.1. Структурная схема системы
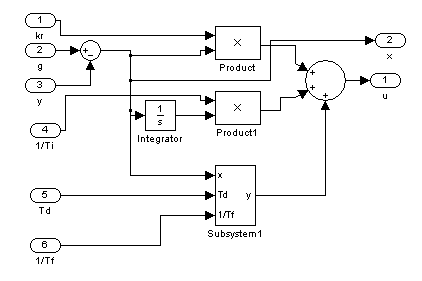
Рис. 6.2. Структурная схема ПИД - регулятора.
Заключение
Таким образом, подводя итог работе, можно отметить, что в ходе её выполнения были определены параметры регулирования системы, включающей в себя нелинейный теплоэнергетический объект (котел для подогрева воды). Были достигнуты следующие результаты:
1. По временным трендам с помощью программы Matlab проведена идентификация данного объекта.
2. Построены все необходимые графики.
3. Рассчитаны показатели качества.
Приложение
clear
% 19-20 Температура смазки dan=xlsread('opertrend');
y=dan(:,19);
u=dan(:,20);
n=length(y);
t=0:3:3*(n-1);
%Вычисление коэффициента передачи
my(1)=y(1);mu(1)=u(1);
for i=2:n
my(i)=my(i-1)+(y(i)-my(i-1))/i;
mu(i)=mu(i-1)+(u(i)-mu(i-1))/i;
ko(i)=my(i)/mu(i);
end
plot(t,ko),grid
%title ('Изменение коэффициента
передачи объекта')
xlabel ('Time, s')
ylabel ('К')
pause
yc=(y-my');
uc=u-mu';
subplot(2,1,1),grid
plot(t,u),grid
title ('Centeres input signal')
ylabel ('U')
subplot(2,1,2),grid
plot(t,y),grid
title ('Centeres output signal')
xlabel ('Time, s')
ylabel ('Y')
pause
% Анализ сигналов объекта
du=std(u)^2;
dy=std(y)^2;
ru=xcorr(uc,'biased');
ry=xcorr(yc,'biased');
ruy=xcorr(uc,yc,'biased');
tau=-n+1:1:n-1;
subplot (3,1,1)
plot(3*tau,ru),grid
title ('Correlation functions')
ylabel ('Ruu')
subplot(3,1,2)
plot(3*tau,ry),grid
ylabel ('Ryy')
subplot(3,1,3)
plot(3*tau,ruy),grid
xlabel ('Time, s')
ylabel ('Ruy')
pause
[S,f]=psd(uc,n,1/3);
subplot(2,1,1)
plot(f(1:10),S(1:10)/max(S)),grid
title ('Spectrs')
ylabel ('Suu')
[S,f]=psd(yc,n,1/3);
subplot(2,1,2)
plot(f(1:10),S(1:10)/max(S)),grid
xlabel ('Frequencies, Hz')
ylabel ('Syy')
pause
subplot(2,1,1)
hist(u,20),grid
title ('Histograms')
ylabel ('Hu')
subplot(2,1,2)
hist(y,20),grid
xlabel ('Intervals, mm')
ylabel ('Hy')
pause
subplot(1,1,1)
% RMNK
m=2;
clear Tp
P=1000*eye(2*m,2*m);
Q=zeros(2*m,1);
F=Q;
for i=1:n-m
F=[-yc(i+m-1:-1:i);uc(i+m-1:-1:i)];
ch=P*F;
zn=1+F'*P*F;
gm=ch/zn;
P=(eye(2*m)-gm*F')*P;
Q=Q+gm*(yc(m+i)-F'*Q);
kf(i,1:2*m)=Q';
Tp(i)=F'*Q;
end
% Анализ ошибки моделирования
e=yc(m+1:end)-Tp';
de=std(e);
plot(t(100:n-m),kf((100:end),:)),grid
title ('Model parametres')
xlabel ('Time, s')
ylabel ('Km')
pause
sr=[yc(m+1:end),Tp'];
plot(t(1:n-m),sr),grid
title ('Model and object outputs')
xlabel ('Time, s')
ylabel ('Y, Yм')
pause
plot (t(1:n-m),e),grid
title ('Model error')
xlabel ('Time, s')
ylabel ('Em')
pause
re=xcorr(e,'biased');
plot(3*tau,ru),grid
title ('Error correlation function')
xlabel ('Time, s')
ylabel ('Ree')
pause
[S,f]=psd(e,n,1/3);
plot(f,S/max(S)),grid
title ('Error spector')
xlabel ('Frequncy, Hz')
ylabel ('Suu')
pause
hist(e,20),grid
title ('Error histogram')
xlabel ('Interval, mm')
ylabel ('Hu')
pause
% Модели объекта
nun=[kf(end,m+1:2*m) 0];
den=[1 kf(end,1:m)];
wod=tf(nun,den,3)
[z,p,k]=zpkdata(wod,'v')
if abs(p(1)-1)<.05
p(1)=1;
end
wodf=zpk(z,p,k,3)
wo=d2c(wodf)
sm=ss(wo)
impulse(wo),grid
pause
step(wo,wodf),grid
pause
bode(wo),grid
pause
nyquist(wo),grid
pause
wonz=zpk(wo)
ym=lsim(wo,uc,t);
f=yc-ym;
%Wc=gram(sm,'c')
%Wo=gram(sm,'o')
K=lqry(sm,100000000,1)
[A,B,C,D]=ssdata(sm);
P=ss(A,[B B],C,[D D]);
Kest=kalman(P,du,0.01)
G=lqgreg(Kest,K);
clsm=feedback(sm,G,+1);
q1=tf(Kest);
q2=tf(G);
impulse(sm,'r-',clsm,'b-'),grid
pause
step(sm,'r-',clsm,'b-'),grid
pause
bode (sm,'r-',clsm,'b-'),grid
pause
nyquist(sm,'r-',clsm,'b-'),grid
save('f','f')
save('wo','wo')
Литература
1. Математическое моделирование: Методы описания и исследования сложных систем. – М.: Наука, 1989.
2. Методы классической и современной теории автоматического управления: Учебник в 3-х т. Т1: Синтез регуляторов и теория оптимизации систем автоматического управления / под ред Н.Д. Егупова. - М.: Изд-во МГТУ им Баумана, 2000. – 736 с.
3. Советов Б.Я., Яковлев С.А. Моделирование систем. – М.: Высшая школа. 1988 (Дополнительная).
4. Александров А.Г. Оптимальные и адаптивные системы. – М: Высшая школа . 1986.
5. Изерман Р. Цифровые системы управления / Пер. с англ. – М.: Мир, 1984. – 541 с.
6. Кашьян Р. Л., Рао А. Р. Построение динамических стохастических моделей по экспериментальным данным. – М: Мир, 1983. 384 с.
7. Ивахненко А. Г., Юрачковский Ю. Г. Моделирование сложных систем по экспериментальным данным. - М.: Радио и связь, 1987. - 120 с.
8. Кендал М. Временные ряды. – М.: Радио и связь, 1981. – 198 с.
Похожие работы
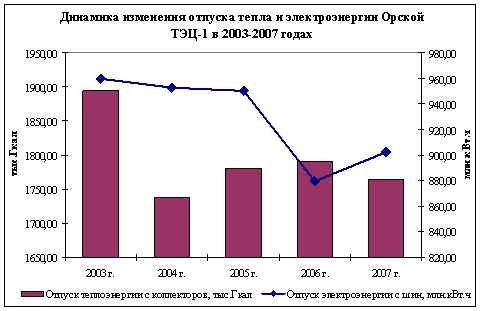
... функционирующий элемент технологического оборудования: механический фильтр, осветлитель, цепочку фильтров блока обессоливания, группу баков и насосов и т.п. 3. Технологическая схема приготовления топлива В котлах Орской ТЭЦ-1 сжигается природный газ, представляющий собой механические смеси различных газов.Состав газа ( в %)а) метан - 97,37б) ...
... VS 24 ат.д.о и после задвижки, медленно открыть ее полностью, также медленно полностью открыть отсечную задвижку VB после турбины. 1.14. Параллельно с началом прогрева турбины включить в работу конденсаторы осевшего пара для чего: - прогреть п/провод до эжектора; - включить по воде конденсатор осевшего пара; - включить в работу эжектор и создать давление в линии отсоса пара уплотнений 0,3 ...
... состава, введенным согласно закону «О городском пассажирском транспорте», договорных отношений между местными властями и транспортными предприятиями. 3. РЕСУРСОСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ НА ГОРОДСКОМ ЭЛЕКТРИЧЕСКОМ ТРАНСПОРТЕ 3.1. Регенерация масел Установки для регенерации отработанных масел и схемы технологического процесса Проводимые исследования кафедрой городского электрического транспорта ( ...
... , что в условиях повышенных требований к защите окружающей среды и расходу топлива дизели остаются наиболее перспективными двигателями. В настоящее время в ФРГ на 14 % автомобилей установлены дизели, во Франции — на каждом третьем автомобиле, а в Австрии — на каждом втором. 2. Система питания автомобиля ПАЗ 4230 2.1 Описание конструкции, принципа работы системы и основных элементов. ...




0 комментариев