Описание объекта управления
Математическое ожидание случайного процесса
Идентификация объекта управления по временным трендам
Основные задачи идентификации
Расчет характеристик математической модели объекта управления
Структурированные модели
Дискретные модели
Выбор и описание закона регулирования
Нелинейные или позиционные регуляторы
Навигация
Расчет характеристик математической модели объекта управления
Разработка системы регулирования температуры смазочного масла турбины
62018
знаков
0
таблиц
34
изображения
4. Расчет характеристик математической модели объекта управления
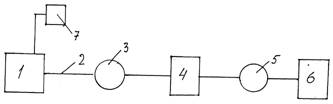
4.1 Математические модели в пространстве состоянийМатематическая модель (образ) представляет собой абстрактное отражение реального объекта (оригинала, прообраза). В зависимости от типа объекта и целей, ради которых строится и используется модель, формальное описание может быть различным. Для моделирования объектов могут быть использованы структурные схемы, операторные уравнения, алгебраические уравнения, дифференциальные, интегральные и интегро-дифференциальные уравнения, Марковские цепи, передаточные функции, частотные характеристики, весовые функции, графы и т. д. Все эти методы функционально связывают входные и выходные сигналы объекта. По количеству входов и выходов объекты и соответствующие им модели разделяют на одномерные и многомерные. Одномерными называют объекты, имеющие один вход и один выход, многомерными – объекты, имеющие несколько входов и выходов, причем число входов не обязательно равно числу выходов. Блок-схемы одномерного и многомерного объектов изображены соответственно на рис. 4.1,а и рис. 4.1,б. Причем число входов не обязательно равно числу выходов.
Рис. 4.1.
Наиболее полно идентифицируемый объект описывается в терминах пространства состояний. Под состоянием объекта понимается совокупность величин xi, полностью определяющих его положение в данный момент времени.
Наиболее употребительной моделью динамических объектов являются дифференциальные уравнения. Будем рассматривать только объекты с сосредоточенными параметрами, которые описываются обыкновенными дифференциальными уравнениями. Порядок системы дифференциальных уравнений, описывающей модель объекта, непосредственно не определяется количеством входов и выходов, а зависит от операторов, преобразующих входные сигналы в выходные.
Для динамических систем, в которых физические процессы протекают непрерывно во времени, скорости изменения переменной состояния объекта можно также задать вектором
, (4.1)
где 
, 
– скорости изменения компонент многомерной переменной состояния.
В свою очередь эти скорости определяются текущими значениями переменной состояния 
, управлениями 
и возмущениями 
, действующими на объект
, (4.2)
где g = (g1, ..., gn)T – вектор функция; x10 , x20. .., xn0 – начальные условия.
Если g( ) – нелинейная функция, то решение уравнения (4.2) усложняется, так как сводится к интегрированию системы нелинейных ДУ. Так как методы интегрирования систем ДУ хорошо разработаны только для линейных систем, то перед работой с ними необходимо линеаризовать g( ) в окрестности рабочей точки, которой соответствует установившейся режим работы объекта.
Для линеаризованной функции g( ) ДУ вида (4.2) с учетом воздействия среды можно представить в векторной форме:
, (4.3)
где A(t); B(t); E(t) – матрицы преобразования, элементы которых в общем случае являются функциями времени.
Элементы xi в уравнении (4.3) называются переменными состояния объекта или фазовыми координатами. Переменные состояния 
(фазовые координаты) образуют вектор состояния, переменные управления и возмущения образуют векторы управления и возмущения. Множество этих векторов составляет пространство состояний (фазовое пространство) X, пространство управлений U и возмущений F.
Во многих физических объектах регулируются, измеряются и передаются по информационным каналам не значения вектора состояния , а другие значения – функции составляющих вектора фазовых координат, называемые управляемыми или выходными величинами. Обозначим измеряемые величины через y1(t), y2(t),..., ys(t), причем обычно s £ n. Тогда уравнение измерения, связывающее регулируемые и фазовые координаты объекта примет вид
. (4.4)
Для линейного объекта это соотношение линейное:
. (4.5)
Матрица С(t) называется матрицей измерения. Она показывает, как изменяются значения вектора состояний при измерении. При измерениях, описываемых выражениями (4.4) и (4.5), вектором выходных сигналов (или просто вектором выхода) является вектор 
. Отметим, что между векторами входа, выхода и состояния существует принципиальное различие. Если все составляющие вектора входа и вектора выхода являются вполне конкретными физическими величинами, то элементами вектора состояния могут быть некоторые абстрактные переменные, физическая природа которых не всегда определена.
Векторно-матричная запись модели линейного динамического объекта с учетом уравнения измерения принимает вид:
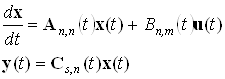. (4.6)
Если матрицы A(t), B(t) и C(t) не зависят от времени, то объект называется объектом с постоянными коэффициентами, или стационарным, объектов. В противном случае объект будет нестационарным.
При наличии погрешностей при измерении, выходные (регулируемые) сигналы задаются линеаризованным матричным уравнением:
, (4.7)
где – вектор регулируемых (измеряемых) величин; C(t) – матрица связи вектора измерений с вектором состояний; v(t) – вектор ошибок измерений (помехи).
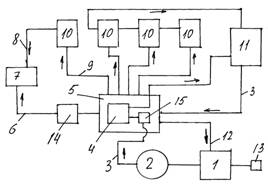
Структура линейной непрерывной системы, реализующая уравнения (4.6) и (2.7) приведена на рис. 4.2.
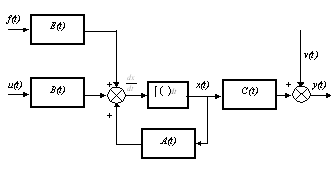
Рис. 4.2.
Данная структура соответствует математической модели объекта построенной в пространстве состояний его входных x(t), u(t), выходных y(t) и внутренних, или фазовых координат x(t).
Похожие работы
... функционирующий элемент технологического оборудования: механический фильтр, осветлитель, цепочку фильтров блока обессоливания, группу баков и насосов и т.п. 3. Технологическая схема приготовления топлива В котлах Орской ТЭЦ-1 сжигается природный газ, представляющий собой механические смеси различных газов.Состав газа ( в %)а) метан - 97,37б) ...
... VS 24 ат.д.о и после задвижки, медленно открыть ее полностью, также медленно полностью открыть отсечную задвижку VB после турбины. 1.14. Параллельно с началом прогрева турбины включить в работу конденсаторы осевшего пара для чего: - прогреть п/провод до эжектора; - включить по воде конденсатор осевшего пара; - включить в работу эжектор и создать давление в линии отсоса пара уплотнений 0,3 ...
... состава, введенным согласно закону «О городском пассажирском транспорте», договорных отношений между местными властями и транспортными предприятиями. 3. РЕСУРСОСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ НА ГОРОДСКОМ ЭЛЕКТРИЧЕСКОМ ТРАНСПОРТЕ 3.1. Регенерация масел Установки для регенерации отработанных масел и схемы технологического процесса Проводимые исследования кафедрой городского электрического транспорта ( ...
... , что в условиях повышенных требований к защите окружающей среды и расходу топлива дизели остаются наиболее перспективными двигателями. В настоящее время в ФРГ на 14 % автомобилей установлены дизели, во Франции — на каждом третьем автомобиле, а в Австрии — на каждом втором. 2. Система питания автомобиля ПАЗ 4230 2.1 Описание конструкции, принципа работы системы и основных элементов. ...
0 комментариев