Движение твердого тела в жидкости

1.3. Движение твердого тела в жидкости

При движении тел в вязкой жидкости возникают силы сопротивления. Происхождение этих сил можно объяснить двумя разными механизмами. При небольших скоростях, когда за телом нет вихрей (ламинарное течение или обтекание), сила сопротивления обуславливается только вязкостью жидкости. Слои жидкости, прилегающие к телу, неподвижны относительно тела. Граничащие с ними слои увлекаются ими по описанному выше механизму вязкого трения в жидкостях. Так создаются силы, тормозящие относительное движение твердого тела и жидкости. Величину этих силы трения можно рассчитать с использованием формулы Ньютона (1).

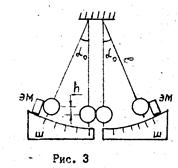
Второй механизм сил сопротивления связан с образованием вихрей (рис.3). Давление в жидкости меняется в зависимости от скорости потока так, что в области вихрей оно существенно уменьшается (уравнение Бернулли: p₁+rv₁²/2=p₂+rv₂²/2 ). Разность давлений Dp=r(v₁² –v₂²)/2 в областях перед телом и за ним создает силу «лобового» сопротивления и тормозит движение тела. Часть работы, совершаемой силами трения при движении тела в жидкости, идет на образование вихрей, энергия которых пере­ходит затем в теплоту.

Если движение тела в жидкости происходит медленно, без образования вихрей, то сила сопротив­ления создается только по первому из описанных механизмов. Для тел сферической формы ее величину определяют по формуле Стокса:

F_c=6phrv (2)

где г - радиус шарика; v - скорость его равномерного движения; h - вязкость жидкости.

2. Экспериментальная часть

Часть I. Определение вязкости жидкости по методу Стокса

Теория метода

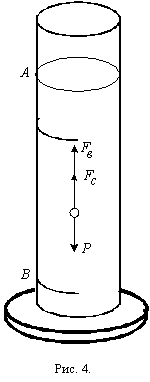
На движущийся шарик в жидкости действуют три силы: сила тяжести - Р, выталки­вающая сила F_A и сила сопротивления Fc. Силу тяжести и выталкивающую силу можно определить через объем шарика, плотность r шарика и плотность r₀ жидкости:

P=4pr³rg/3 (3)

F_A =4pr³r_o g/3 (4)

Сила тяжести и выталкивающая сила постоянны. При малой скорости падения шари­ка сила сопротивления прямо пропорциональна этой скорости и поэтому на начальном этапе он движется равноускоренно. Затем наступает момент, когда все три силы уравновешиваются, и шарик начинает двигаться равномерно:

P=F_A + F_c  или 4pr³rg/3= 4pr³r_o g/3+6phrv, (5)

 откуда

(6)

Экспериментальная установка

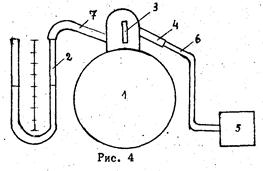
Для определения вязкости жидкости по методу Стокса берется высокий цилиндрический сосуд с исследуемой жидкостью (рис.4). На сосуде имеются две кольцевые метки А и В. Метка А соответствует той высоте, где силы, действующие на шарик, уравновешивают друг друга и движение становится равномерным. Нижняя метка В нанесена для удобства отсчета времени в момент падения шарика.

Бросая шарик в сосуд, отмечают по секундомеру время t прохождения шариком расстояния l = АВ между двумя метками.

Если в формулу (6) подставить выражение для скорости движения v=l/t и вместо радиуса r ввести диаметр шарика d, то окончательная расчетная формула приобретает вид:

( 7)

Ход выполнения работы

1. Измерьте расстояние между метками А и В.

2. При необходимости измерьте с помощью ареометра плотность жидкости r₀.

3. Измерьте микрометром или штангенциркулем диаметр d шарика.

4. Бросив шарик в сосуд с жидкостью, измерьте время t прохождения шариком рас­стояния между метками А и В.

5. По формуле (7) вычислите вязкость жидкости h.

6. Аналогичные измерения проделайте с пятью шариками. Результаты измерений и вычислений заносите в таблицу 1 отчета.

7. По результатам всех опытов найдите среднее значение вязкости h.

8. Для оценки систематической погрешности измерения вязкости используйте расчетную формулу (7). Выведите формулу для вычисления относительной погреш­ности измерения. При этом условно считается, что табличные величины, входящие в формулу, не имеют погрешностей, а погрешности измеренных величин /, d, r опре­деляются точностью приборов, использованных для их измерения.

9. Полученное значение вязкости сравните с табличной величиной для дан­ной жидкости. При объяснении причин расхождения укажите какой из используемых измерительных приборов вносит в окончательный результат наибольшую погрешность.

Часть II. Определение вязкости воздуха по методу Пуазейля

Теория метода

При ламинарном движении жидкостей и газов по гладким цилиндрическим трубам расход (объем жидкости или газа, протекающих через поперечное сечение трубы за одну секунду), зависит от ее вязкости, диаметра трубы, ее длины и разности давления на ее концах. Соответствующее соотношение было выведено Пуазейлем и носит его имя.

V=Dp pr²Dt/hl ,

куда входят перепад давления, радиус трубы, длительность течения, коэффициент вязкости, длина трубы.

На основании этого соотношения разработан и широко применяется метод измерения вязкости жидкостей и газов - метод Пуазейля.

Для газов он состоит в измерении скорости ламинарного протекания газов в тонком капилляре с известными размерами и при контролируемой разности давлений. В данной работе по методу Пуазейля определяется вязкость воздуха. На величину вязкости газов большое влияние оказывают посторонние примеси. Для атмосферного воздуха, например, следует учитывать содержание водяных паров. В установках для точных измерений воздух перед поступлением в капилляр осушают различными, чаще всего химическими осушителями. Важно также помнить, что вязкость газов в большой степени зависит от их температуры, что также предусмотрено в лабораторных приборах.

Экспериментальная установка

Экспериментальная установка для определения воздуха (рис. 4) состоит из сосуда 1 со сливным шлангом 2, капилляра 3, мерительного стакана 4 и жидкостного манометра 5. Перед опытом сосуд заполняется водой. При опущенном шланге 2 уровень воды в со­суде уменьшается и возникает перепад давлений воздуха на концах А и В капилляра 3, который измеряется манометром 5. Освободившийся объем занимает воздух, прони­кающий в сосуд через капилляр. При этом объем вытекшей воды равен объему воздуха, прошедшему через капилляр.

Расчетная формула для определения коэффици­ента вязкости по методу Пуазейля имеет вид:

(8)

где d- диаметр капилляра, / - его длина, V- объем прошедшего через капилляр воздуха (объем вы­текшей из сосуда жидкости), Dр - перепад давле­ний на концах капилляра (показание манометра), t - время протекания воздуха через капилляр.

Ход выполнения работы

1. Закрепите сливной шланг в вертикальном по­ложении. Заполните сосуд 7 водой до начала его конической части. Плотно закрепите пробку с капилляром в горловине сосуда.

2. Опустите сливной шланг вниз, подставив под него мерный сосуд. Измерьте секундомером время t, в течение которого из сосуда вытечет объем V=200 см³ воды.

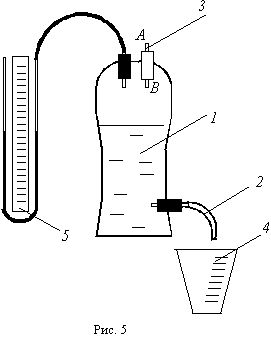3. Измерьте в это же времени перепад давлений Dр по манометру.

Примечание: При постепенном понижении уровня воды в сосуде скорость истечения уменьшается. Это приводит к изменению перепада давлений воздуха на концах капил­ляра. Поэтому необходимо брать среднее за время опыта значение Dр.

4. По формуле (8) вычислите вязкость воздуха.

5. Опыт повторите не менее трех раз. Результаты занесите в таблицу 2 отчета.

6. Оцените относительную погрешность измерения вязкости воздуха. Погрешности измерений диаметра и длины капилляра возьмите из «паспорта» прибора.

9. В выводе сравните полученное значение вязкости воздуха с табличным значением (h= 1,8×10^-5 Па×с при 18^оС)

Дополнительное задание

1. Вычислите плотность воздуха по формуле , где М = 0,029 кг/моль – молярная масса воздуха, R - универсальная газовая постоянная, давление и температура - нормальные.

2. Вычислите среднюю арифметическую скорость молекул воздуха при данных условиях .

3. Вычислить среднюю длину свободного пробега  молекул воздуха при нормаль­ных условиях, исходя из формулы Максвелла .

Похожие работы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ (МЕХАНИКА И ТЕРМОДИНАМИКА)

Скачать

89077

4

25

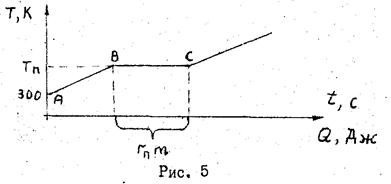
... изменение. 3. Что такое термодинамическая вероятность состояния (статис­тический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...

Уровневый подход к физике

Скачать

8952

1

0

... случайность, спонтанность непредсказуемость развития процесса (своего рода физический экзистенциализм), и в силу этого он далек от парадигмы абсолютности. Рассмотрим уровневый подход на примере энергии. Сегодня основные виды энергии в физике рассматриваются по парам: потенциальная – кинетическая, электрическая – магнитная, тепловая – механическая, причем каждая пара рассматривается автономно, ...

Механика, молекулярная физика и термодинамика

Скачать

121629

26

25

... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...

Программа вступительных экзаменов по физике в 2004г. (МГУ)

Скачать

13869

0

0

... . Фронт волны. Интерференция волн. Принцип Гюйгенса. Дифракция волн. Уравнение бегущей волны. Стоячие волны. Звуковые волны. Скорость звука. Громкость и высота звука. II. Молекулярная физика и термодинамика II.1. Основы молекулярно-кинетической теории Основные положения молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Массы и размеры молекул. Моль вещества. ...