Эффективный диаметр молекул воздуха: d = … м

6. Эффективный диаметр молекул воздуха: d = … м

Цель работы:

Углубление теоретических представлений об энтропии, экспериментальное наблюдение процесса плавления и кристаллизации и получение навыков измерения изменения энтропии.

1. Теоретическая часть

Термодинамический процесс обратим, если, протекая в обратном направлении, он возвращает систему в исходное состояние без затрат энергии (упругий удар, колебания маятника в отсутствии сопротивления, идеализированный цикл Карно). Большинство процессов в технике – необратимы или, по крайней мере, содержат этапы, являющиеся необратимыми (неупругий удар, процессы с трением, диффузия, теплообмен). Энтропия является количественной мерой степени необратимости процесса.

Из равенства КПД тепловых двигателей и термического КПД обратимого цикла Карно

(1)

можно получить выражение

(2)

Это выражение означает, что количество теплоты, полученное или отданное телом при обратимом процессе, пропорционально температуре. Отношение Q/T называется приведенным количеством теплоты. Сумма приведенных количеств теплоты при любом обратимом процессе равна нулю, что в дифференциальной форме имеет вид

,  (3)

причем интеграл берется по замкнутому контуру (круговой процесс). В каждом цикле кругового процесса все термодинамические параметры принимают исходные значения, т.е. их изменение равно нулю. В этом случае равна нулю и сумма приведенных количеств теплоты, что позволяет ввести термодинамический параметр состояния энтропию S, как некоторую функцию состояния, дифференциал которой

(4)

Если некоторая термодинамическая система обратимо переходит из состояния 1, характеризующегося параметрами р₁, V₁, Т₁, в состояние 2 с параметрами р₂, V₂, Т₂, то изменение энтропии системы при таком переходе может быть вычислено по формуле

, (5)

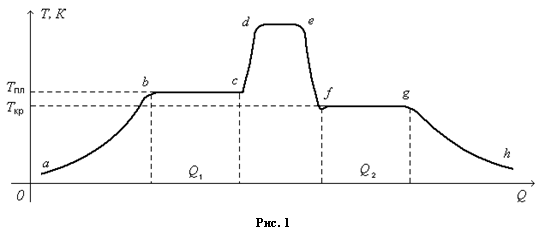
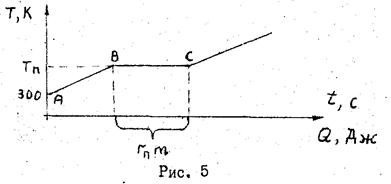
где dQ — элементарный приток теплоты в систему, Т - термодинамическая температура всей системы. Интеграл берется вдоль «траектории» процесса, например абс при нагревании и плавлении, как показано на рисунке 1.

Возможны следующие три случая:

а) DS=0 – процесс обратим, может протекать как в прямом, так и в обратном направлениях;

б) DS>0 - процесс необратим, самопроизвольно протекает только в одном направлении

в) DS<0 - процесс самопроизвольно протекать не может, необходим подвод энергии извне.

2-й закон термодинамики с использованием понятия энтропии формулируется так:

Все процессы в природе протекают в направлении увеличения энтропии, энтропия замкнутой системы не может самопроизвольно уменьшаться.

В статистической физике энтропию связывают с термодинамической вероятностью состояния системы – с числом способов, которыми может быть реализовано данное состояние макроскопической системы. Согласно Больцману энтропия системы и термодинамическая вероятность связаны между собой следующим соотношением

S=klnW, (6)

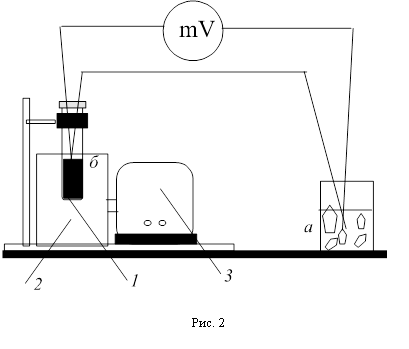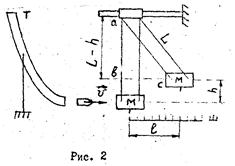
где k – постоянная Больцмана. Энтропия является мерой неупорядоченности системы. 2. Экспериментальная часть Установка собрана по схеме, показанной на рисунке 2. Она состоит из электронагревателя малой мощности 2 (трубчатая муфельная печь), питание которого осуществляется через понижающий трансформатор 3. В стеклянной пробирке находится небольшой кусочек олова известной массы 1. Пробирка закреплена в штативе и может опускаться в нагреватель или подниматься из него. Температуру олова измеряют дифференциальной термопарой. Она состоит из двух термопар, включенных «навстречу» так, что милливольтметр показывает разность термоЭДС. При этом температура t₁ «холодного спая» термопары должна быть постоянной и вполне определенной, для чего этот спай термопары рекомендуется погружать в тающий лед. Искомая температура t₂  определяется по градуировочному графику этой термопары или с помощью градуировочного коэффициента. Используемая в данной работе термопара в требуемом интервале температур имеет градуировочный коэффициент a =19,5 град/мВ.

Если «холодный» спай термопары находится не в тающем льду, а в воздухе, то к полученным из градуировки результатам необходимо приплюсовать комнатную температуру. В качестве электроизмерительного прибора используется мультиметр, который включается на измерение постоянного напряжения на пределе 200 мV.

В данной лабораторной работе определяется изменение энтропии, происходящее при нагревании и плавлении (или при охлаждении и затвердевании) определенной массы олова.

Возрастание энтропии при нагревании можно объяснить возрастанием энергии колебательного движения атомов олова в кристаллической решетке, что приводит к увеличению возможных микросостояний и, следовательно, к росту энтропии, как меры неупорядоченности системы. При плавлении энтропия системы возрастает дополнительно за счет неупорядоченности пространственного распределения атомов в жидкой фазе.

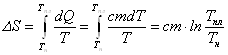
Если первоначально температура олова равна комнатной, то при подведении теплоты олово сначала нагревается до температуры плавления, потом плавится при постоянной температуре. Изменение энтропии на первом этапе – в процессе нагревания, равно:

(7)

где Т_пл - температура плавления, Т_н—начальная температура кристаллической фазы, с - удельная теплоемкость олова: с = 2,3 • 10² Дж/(кг ×К), m - масса олова.

На втором этапе - при плавлении, изменение энтропии определяется по формуле:

 (8)

 

где l — удельная теплота плавления (для олова l=5,85×10⁴ Дж/кг).

Полное изменение энтропии равно:

(9)

Эта величина положительна DS >0, если рассматриваемый процесс сопровождается притоком теплоты в систему, т.е. при нагревании и плавлении. При кристаллизации и охлаждении DS<0. Для вычисления DS надо знать параметры, входящие в (9), в частности, необходимо измерить температуру плавления и температуру кристаллизации олова.

Измерения и обработка результатов

1. Изучите описание экспериментальной установки. При работе особое внимание уделить технике безопасности:

·  Включайте нагреватель только с разрешения преподавателя.

·  Не касайтесь металлических деталей установки во время его работы. Опасайтесь ожогов.

·  Прежде, чем производить любые манипуляции с прибором выньте вилку трансформатора из розетки.

2. Подготовьте прибор к работе. Для этого опустите пробирку с оловом в горловину печи. Подключить мультиметр к гнездам термопары, выставив его на 200mV постоянного напряжения.

3. Включите прибор (с разрешения преподавателя). Через каждые 20 –30 секунд записывайте показания мультиметра. Данные заносите в таблицу 1 отчета. Когда милливольтметр покажет 12 – 13 мВ, процесс нагревания остановите, отключив электропечь.

4. Для охлаждения образца поднимите его и отведите в сторону от электропечи. Для этого отверните винт крепления муфты штатива, поверните держатель пробирки и закрепить его в новом положении.

5. Произведите измерения температуры в процессе охлаждения образца. Для этого вновь необходимо отмечать показания милливольтметра через каждые 20-30 секунд. Этот процесс завершите при показаниях милливольтметра 4 – 5 мВ. (таблица 2)

6. Пользуясь градуировочным коэффициентом, переведите показания милливольтметра в градусы Цельсия с учетом комнатной температуры. Заполнить соответствующую строку в таблицах 1 и 2.

7. По полученным результатам постройте графики изменения температуры олова со временем t^о=f(t). Желательно, чтобы в верхней части графики нагревания и охлаждения кончались и начинались из одной точки.

8. Вновь включите электропечь и повторно снимите данные для построения кривых нагревания-плавления и кристаллизации-охлаждения олова. Заполнить таблицы 3 и 4. Постройте на прежней координатной сетке новые графики t^о=f(t). По горизонтальным участкам всех четырех кривых определите среднее значение температуры фазовых переходов: плавления Т_пл и кристаллизации Т_кр (по шкале Кельвина).

9. По данным эксперимента, используя выражения (7-9), вычислите:

·  Изменение энтропии DS₁ данного образца олова при изменении температуры от комнатной до температуры плавления олова.

·  Изменение энтропии этого образца DS₂ при плавлении олова.

·  Полное изменение энтропии в процессе нагревания и плавления образца.

·  Изменение энтропии DS₃ данного образца олова при кристаллизации образца.

·  Изменение энтропии DS₄ данного образца олова при охлаждении образца от температуры кристаллизации до конечной температуры.

·  Полное изменение энтропии образца при его кристаллизации и охлаждении.

Контрольные вопросы

1.  Какими энергетическими превращениями сопровождается процесс плавления? Процесс кристаллизации?

2.   Приведите примеры обратимых и необратимых термодинамиче­ских процессов.

3.  Каков физический смысл «приведенной теплоты»? Почему в необратимых процессах сумма приведенных количеств теплоты не равна нулю?

4.  Почему имеет смысл изменение энтропии, а не ее значение?

5.   Каков вероятностный смысл понятия энтропия? Приведите примеры.

6.  Как рассчитать изменение энтропии при нагревании? При фазовом переходе в веществе?

7.   Каков принцип действия термопары? Дифференциальной термопары?

Отчет по лабораторной работе № 5

«Изучение изменения энтропии в неизолированной системе»

выполненной студент . . . . . курса, ...... Ф. И. ...........

группа …. «…»…………. 200...г.

Цель работы: .............................................................................................................................

Масса образца m = .... кг

Удельная теплоемкость олова  с = .... Дж/кг×К

Удельная теплота плавления олова l = ... Дж/кг

Комнатная температура t_к = ... °С

Таблица 1

t, c

U, мВ

t°C

Таблица 2

t, c

U, мВ

t°C

Таблица 3

t, c

U, мВ

t°C

Таблица 4

t, c

U, мВ

t°C

Расчет изменения энтропии

При нагревании образца: Т_н = ... К, Т_пл = ... К, DS₁ = ... Дж/К

При плавлении образца: Т_пл = ... К DS₂ = ... Дж/К

Полное изменение при нагревании и плавлении: DS = ... Дж/К

При кристаллизации образца: Т_кр = ... К, Т_к = ... К, DS₃ = ... Дж/К

При охлаждении образца: Т_кр = ... К, Т_к = ... К, DS₄ = ... Дж/К

Полное изменение при кристаллизации и охлаждении: DS = ... Дж/К

Выводы: ………………………………………………………………………………………..

[1] Анализ формулы (13) показывает наличие минимума у периода колебаний при ml²=J₀.

[2] Оценка погрешности измерения производится по данным первого опыта с указанием погрешностей всех величин, входящих в расчетную формулу. В окончательный результат вносится среднее по всем опытам значение вязкости.