Исследование зависимости ускорения от силы при постоянной массе
Исследование зависимости ускорения от массы при постоянной силе
Экспериментальная установка
Зависимость углового ускорения e от действующего момента
Зависимость углового ускорения от момента действующих сил при J = const
Зависимость углового ускорения от момента инерции при M = const
Теоретическая часть
Теоретическая часть
Теоретическая часть
Теоретическая часть
Движение твердого тела в жидкости
Исходя из формулы р = nkT , вычислить концентрацию п молекул воздуха при нормальных условиях (k - постоянная Больцмана)
Эффективный диаметр молекул воздуха: d = … м
Навигация
Теоретическая часть
Физика: механика и термодинамика
67410
знаков
17
таблиц
19
изображений
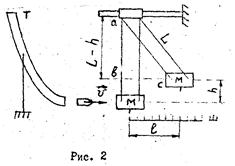
2.1. Теоретическая часть Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О, не проходящей через центр масс С тела (рис.2).
Если маятник выведен из положения равновесия на некоторый угол j, то составляющая
силы тяжести 
уравновешивается силой реакции оси О, а составляющая 
стремится возвратить маятник в положение равновесия. Все силы приложены к центру масс тела. При этом
. (7)
Знак минус означает, что угловое смещение j и возвращающая сила имеют противоположные направления. При достаточно малых углах отклонения маятника из положения равновесия sinj »j, поэтому сила Ft» -mgj и она ведет себя подобно упругим силам.
Поскольку маятник в процессе колебаний совершает вращательное движение относительно оси О, то оно может быть описано основным законом динамики вращательного движения
, (8)
где М – момент силы Ft относительно оси О, J – момент инерции маятника относительно оси О, 
- угловое ускорение маятника.
Момент силы в данном случае равен
M = Ft×l = -mgj×l , (9)
где l – расстояние между точкой подвеса и центром масс маятника.
С учетом (9) уравнение (8) можно записать в виде
(10)
или
, (11)
где 
Решением дифференциального уравнения (11) является функция
j =j0×cos(w0t+a) , (12)
позволяющая определить положение маятника в любой момент времени t. Из выражения (12) следует, что при малых колебаниях физический маятник совершает гармонические колебания с амплитудой колебаний j0, циклической частотой 
, начальной фазой a
и периодом
T=2p/w0= 2p{J0+ml2)/mgl}1/2, (13)
Анализ формулы (13) позволяет сформулировать следующие закономерности колебаний физического маятника:
При малой амплитуде и в отсутствие сторонних сил
1. период колебаний физического маятника зависит от момента инерции маятника относительно оси вращения (качания);
2. период колебаний физического маятника при малых смещениях не зависит от амплитуды колебаний;
3. период колебаний физического маятника сложным образом зависит от положения центра масс маятника относительно точки подвеса[1].
2.2. Экспериментальная часть
Применяемые в данной работе физические маятники представляют собой:
1) однородный стержень, достаточно длинный, чтобы момент инерции относительно центра его массы можно было рассчитывать по формуле J0 = ml2/12;
2) плоские тела правильной геометрической формы, момент инерции которых может быть рассчитан исходя из их геометрии и массы.
Стержни закрепляются в специальной оправе с призматическим основанием, и после установки на платформу превращаются в маятники.
Плоские тела имеют отверстия для подвешивания на ось вращения.
Период колебаний маятника измеряют с помощью секундомера.
Задание 1. Изучение зависимости периода колебаний физического маятника от его
момента инерции и расстояния между осью качаний и центром тяжести
маятника
1. Закрепите оправу на конце стержня и установите его на вилку. Измерьте расстояние l1 от оси качаний до центра тяжести стержня.
2. Отклоните стержень на 5 -6° и измерьте время 5-10 полных колебаний. Определите период колебаний.
3. Переместите оправу ближе к центру тяжести стержня. Измерьте расстояние l2. Снова измерьте период колебаний стержня.
4. Тем же образом необходимо провести 5-6 опытов, постепенно перемещая опорную призму к середине стержня. Все результаты измерений занесите в таблицу 2.1. отчета.
4. По результатам опыта вычислите величины l2 и (T2l).
5. Следует построить два графика. Первый график зависимости T=f(l) отображает сложную зависимость периода колебаний физического маятника от его момента инерции и расстояния до оси качания. Второй график – линеаризация той же зависимости. Если точки на втором графике ложатся на прямую с небольшим разбросом, что объясняется погрешностями измерений, то можно сделать вывод о правильности формулы (13) для периода колебаний физического маятника.
Задание 2. Определение моментов инерции тел различной формы методом
колебаний.
1. Из набора тел к работе возьмите (по указанию преподавателя) одно и измерьте период его колебаний относительно произвольной оси.
2. С помощью формулы (16) вычислите момент инерции тела относительно оси качаний.
3. Произведите необходимые геометрические измерения и, зная массу тела, вычислите момент инерции тела относительно центра масс. С помощью теоремы Гюйгенса – Штейнера рассчитайте момент инерции тела относительно оси, проходящей через ось качаний.
4. Величину моментов инерции, полученных при измерении, сравните с рассчитанными теоретически. Для корректного заключения следует оценить погрешности измеренного и вычисленного моментов инерции. Относительная погрешность измеренного момента инерции находится по формуле:
(14)
Относительная погрешность вычисленного момента инерции определяется из расчетной формулы для заданного вам тела и погрешностей, входящих в нее величин.
Контрольное задание. Определение ускорения свободного падения и длины стержня
С помощью полученного графика зависимости (T2l) = f(l2), можно определить ускорение свободного падения и длину стержня, используемого в опыте. Для этого следует определить угловой коэффициент наклона прямой и величину отрезка, отсекаемого прямой от оси OY:
(15)
При вычислении длины стержня используйте экспериментально полученное значение ускорения свободного падения.
В выводе сравните полученные величины g и d с их действительными значениями.
Часть III. Крутильный маятник
Похожие работы
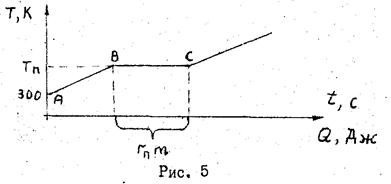
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... случайность, спонтанность непредсказуемость развития процесса (своего рода физический экзистенциализм), и в силу этого он далек от парадигмы абсолютности. Рассмотрим уровневый подход на примере энергии. Сегодня основные виды энергии в физике рассматриваются по парам: потенциальная – кинетическая, электрическая – магнитная, тепловая – механическая, причем каждая пара рассматривается автономно, ...
... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...
... . Фронт волны. Интерференция волн. Принцип Гюйгенса. Дифракция волн. Уравнение бегущей волны. Стоячие волны. Звуковые волны. Скорость звука. Громкость и высота звука. II. Молекулярная физика и термодинамика II.1. Основы молекулярно-кинетической теории Основные положения молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Массы и размеры молекул. Моль вещества. ...
0 комментариев