Зависимость углового ускорения e от действующего момента

2.1. Зависимость углового ускорения e от действующего момента

силы М при постоянном моменте инерции системы J = const

1. Заранее измерьте высоту h падения груза, которая может быть оставлена во всех последующих опытах одинаковой.

2. Укрепите цилиндры m₁на стержнях на минимальном расстоянии от оси вращения. Сбалансируйте маятник.

3. Первый опыт проводится при минимальном значении массы груза m. Намотайте нить на шкив. Расположите нижний край груза на уровне верхней метки. Отпустите груз, предоставив ему возможность падать. Засеките время падения груза. Измерения повторите трижды. Значения m, r, h и среднее значение времени заносите в таблицу 1 отчета.

4. Измените значение момента сил М_н, увеличив массу груза. Снова трижды измерьте времени падения. (Момент силы можно также изменить, перенеся нить на шкив другого радиуса).

5. Проведите еще не менее трех опытов, постепенно увеличивая момент силы М_н.

6. Пользуясь формулами (4), (5), (8), определите для каждого опыта значения линейного ускорения а, углового ускорения e и момента силы натяжения нити М_н. Завершите заполнение таблицы 1.

Обсуждение результатов, полученных в опытах 2.1

Постройте график зависимости углового ускорения e от момента силы М_н при постоянном моменте инерции J=const. (график 1).

Поскольку e= f(М_н) – линейная функция (см. (3)), то ее графики в координатных осях [М,e,] - прямые линии. Если экспериментальные точки не ложатся на прямую, график надо провести так, чтобы «разброс» точек был приблизительно одинаков по обе стороны прямой. Если «разброс» мал, то это свидетельство того, что угловое ускорение действительно прямо пропорционально моменту сил, приложенных к вращающемуся телу, что подтверждает закон динамики вращательного движения.

Если разброс велик и это затрудняет построение графика, обработайте результаты методом наименьших квадратов или проделайте новую серию измерений.

2.2. Зависимости углового ускорения e от момента

инерции J системы при постоянном моменте силы М=const.

1. Все измерения в данном опыте должны проводятся при неизменном значении момента силы M_н, который зависит не только от массы груза m, радиуса шкива R, но и от ускорения падения груза (формула (10)). Но поскольку ускорение а оказывается гораздо меньше ускорения свободного падения g (что видно по результатам первого опыта), момент силы М_н можно считать приблизительно постоянным, если не менять значения m и R. При этом его можно вычислять по формуле:

(12)

Таким образом, масса груза и радиус шкива во всех последующих опытах берутся одинаковыми.

2. Укрепите цилиндры m₁на стержнях на минимальном расстоянии от оси вращения. Сбалансируйте маятник. Измерьте расстояние r от середины подвижных цилиндров до оси вращения. Вычислите по формуле (10) момент инерции маятника в данном случае.

2. Трижды проведите измерение времени падения груза. Используя среднее значение времени падения, рассчитайте по формулам (4) и (5) линейное и угловое ускорение.

3. Переместите цилиндры m₁ на стержнях на несколько сантиметров. Проверьте балансировку маятника. Измерьте расстояние r и вычисляют момент инерции маятника. Измерьте время падения груза.

4. Вновь переместите цилиндры на стержне, сбалансируйте маятник, вычислите момент инерции и измерьте время падения груза. Шаг перемещения цилиндров должен быть выбран таким образом, чтобы получить еще 3-4 значения момента инерции маятника. Заполните таблицу 2 отчета.

Обсуждение результатов, полученных в опытах 2.2.

В соответствии с законом динамики угловое ускорение обратно пропорционально моменту инерции, т. е. график зависимости e = f(J) представляет собой гиперболу и визуально не идентифицируется. Поэтому проверку зависимости e =f(J) лучше провести в координатных осях [e,J^-1]. В этом случае график должен представлять собой прямую линию, проходящую через начало координат. Поэтому следует вычислить величины J^-1 = 1/J и построить соответствующий график 2.

Если построенный по вашим измерениям график e = f(J^-1) представляет собой прямую линию, то этот факт подтверждает справедливость второй части закона динамики вращательного движения – угловое ускорение обратно пропорционально моменту инерции вращающегося тела.

Если разброс велик и это затрудняет построение графика, обработайте результаты методом наименьших квадратов или проделайте новую серию измерений.

Дополнительная проверка достоверности результатов

Определение момента силы трения, действующей в системе

1. В идеальном случае все графики e=f(M_н) должны проходить через начало координат. Однако реальные прямые отсекают некоторое значение момента сил – существует некоторое минимальное значение момента сил, которое соответствует началу движения маятника. Координата этой точки дает величину момента силы трения скольжения в подшипнике маятника.

Определите по графику 1 значение момента силы трения и сравните полученный результат с М_тр, измеренном ранее в задании 1.

2. Угловой коэффициент наклона графика 1 равен моменту инерции маятника в данной его конфигурации: J=DM/De.

Определите момент инерции системы по графику и сравните с его значением, рассчитанным по формуле (10) для этой конфигурации. Если между ними есть различие, то объясните причину и укажите границу погрешности измерений.

3. Угловой коэффициент наклона графика 2 равен моменту приложенных к маятнику сил: .

Определите по графику момент сил, приложенных к маятнику, и сравните его со значением, рассчитанным по формуле (12.)

Контрольные вопросы и упражнения

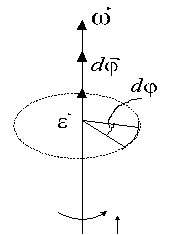
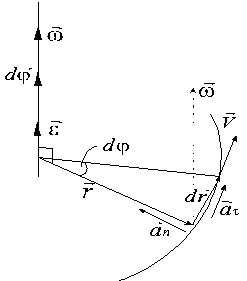
1. Назовите основные характеристики вращательного движения, укажите их обозначения, дайте им определения и назовите единицы измерения. Выделите из них векторные.

2. Запишите уравнения, свзывающие угловую и линейную скорости, угловое и линейное ускорение, период и частоту.

3. Дайте определение момента инерции материальной точки. Назовите единицы измерения момента инерции.

4. Дайте определение момента силы, укажите его направление и назовите единицы измерения.

5. Что исследовалось в данной работе? Из каких заданий состоит вся работа? Как выполняется задание 1? Задание 2? Задание 3?

6. Каковы погрешности использованной в работе экспериментальной установки?

7. Какие выводы сделаны вами на основании анализа экспериментальных результатов?

8. Выполните дополнительно следующие задания контрольного характера.

8.1. Момент силы трения: По результатам задания 1

По графику 1

8.2. Момент инерции системы: По результатам вычислений

По графику 1

8.3. Момент силы:  По результатам вычислений

По графику 2

Отчет по лабораторной работе № 2

«Изучение вращательного движения»

выполненной студент . . . . . курса, …...... Ф. И. ...........

группа …. «…»…………. 200...г.

Цель работы: .............................................................................................................................

Задание 1. Определение момента силы трения

m₀ = …. кг, R = … м, М_тр = Н×м

Задание 2. Проверка основного уравнения динамики вращательного движения

Похожие работы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ (МЕХАНИКА И ТЕРМОДИНАМИКА)

Скачать

89077

4

25

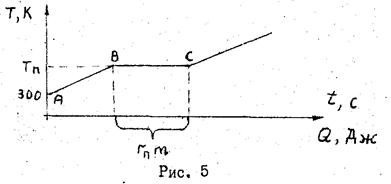
... изменение. 3. Что такое термодинамическая вероятность состояния (статис­тический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...

Уровневый подход к физике

Скачать

8952

1

0

... случайность, спонтанность непредсказуемость развития процесса (своего рода физический экзистенциализм), и в силу этого он далек от парадигмы абсолютности. Рассмотрим уровневый подход на примере энергии. Сегодня основные виды энергии в физике рассматриваются по парам: потенциальная – кинетическая, электрическая – магнитная, тепловая – механическая, причем каждая пара рассматривается автономно, ...

Механика, молекулярная физика и термодинамика

Скачать

121629

26

25

... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...

Программа вступительных экзаменов по физике в 2004г. (МГУ)

Скачать

13869

0

0

... . Фронт волны. Интерференция волн. Принцип Гюйгенса. Дифракция волн. Уравнение бегущей волны. Стоячие волны. Звуковые волны. Скорость звука. Громкость и высота звука. II. Молекулярная физика и термодинамика II.1. Основы молекулярно-кинетической теории Основные положения молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Массы и размеры молекул. Моль вещества. ...