Навигация
Теоретическая часть
3.1. Теоретическая часть
Крутильный маятник представляет собой стержень, шнур или проволоку, один, (как правило – верхний) конец которой закреплен. К нижнему концу подвешивается тело произвольной формы. Если повернуть на некоторый угол груз с проволокой вокруг ее длинной (вертикальной) оси, и отпустить, то в системе возникнут крутильные колебания. Дифференциальное уравнение малых крутильных колебаний в отсутствие трения имеет привычный вид
![]() (16)
(16)
По аналогии с пружинным маятником, для которого ![]() (k – коэффициент упругости, m – масса, как мера инертности), для крутильного маятника может быть записано
(k – коэффициент упругости, m – масса, как мера инертности), для крутильного маятника может быть записано ![]() , где f – коэффициент упругости кручения подвеса, J – момент инерции груза.
, где f – коэффициент упругости кручения подвеса, J – момент инерции груза.
Таким образом, если масса проволоки ничтожна в сравнении с грузом, то период гармонических колебаний крутильного маятника зависит от момента инерции подвешенного тела и от упругих свойств материала подвеса:
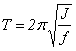 (17)
(17)
Между коэффициентом f упругости кручения образца и модулем сдвига G материала этого образца существует следующее соотношение
![]() , (18)
, (18)
где d – диаметр цилиндрической проволоки, L – ее длина.
3.1. Экспериментальная часть
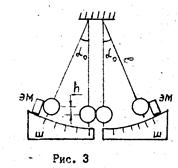
В данной работе крутильный маятник (рис 3) представляет собой шнур или проволоку длиной до 1 м, верхний конец которой закреплен в зажиме, например, прибит к верхней части проема двери. На нижнем конце имеется легкая горизонтальная платформа, в которой закрепляется груз. Грузы имеют правильную геометрическую форму (стержни) и известную массу, что облегчает расчет их моментов инерции.
Задание 1. Определение зависимости периода колебаний
крутильного маятника от момента инерции груза.
1. Штангенциркулем измерьте диаметр проволоки, а линейкой ее длину.
2. Измерьте длину стержня и, по известной массе, рассчитайте его момент инерции.
3. Укрепите стержень в платформе так, чтобы он располагался горизонтально, а центр его тяжести совпадал с линией подвеса.
4. Сообщите маятнику вращательный импульс так, чтобы он совершал крутильные колебания с небольшой амплитудой. Измерьте суммарное время 5-10 колебаний маятника. Вычислите период колебаний.
5. Проделайте подобные измерения и расчеты с другими телами из набора. Результаты занесите в таблицу 3.1 отчета.
6. Постройте график зависимости T(J) в координатных осях [J,T2].
7. По виду графика сделайте вывод о характере зависимости T(J) для крутильного маятника.
Задание 2. Определение модуля сдвига материала методом крутильных колебаний
1. Используя вычисленный ранее момент инерции стержня и период колебаний по формуле (17) рассчитайте коэффициент упругости кручения f подвеса.
2. По формуле (18) рассчитайте модуль сдвига G материала проволоки.
3. Замените проволоку (материал – по указанию преподавателя) и, проделав необходимые измерения, определите коэффициент упругости кручения f и модуль сдвига G ее материала.
4. Рассчитайте абсолютную и относительную погрешности измерений величин f и G.
5. Сравните полученные значения модуля сдвига с табличными значениями и сделайте вывод о точности проделанных измерений. В выводе следует также проанализировать, какая из измеряемых величин вносит наибольшую погрешность в результат измерения.
Задание 3. Определение моментов инерции тел методом крутильных колебаний
1. Подвесив исследуемое тело (кольцо с указанной на нем массой) к проволоке и известным коэффициентом упругости кручения, измерьте период колебаний.
2. По формуле 15 рассчитайте момент инерции исследуемого тела относительно оси, совпадающей с осью проволоки.
3. Рассчитайте момент инерции кольца по его массе и радиусу относительно этой же оси вращения.
4. Сравните экспериментальный и теоретический результаты.
Контрольные вопросы
1. Дайте определение гармонических колебаний и приведите примеры.
2. Какие величины характеризуют гармонические колебания?
3. Запишите дифференциальное уравнение свободных гармонических колебаний.
4. Дайте строгое определение математического маятника и опишите закономерности его колебаний.
5. Какие упражнения были выполнены вами с этим маятником?
6. Дайте строгое определение физического маятника и опишите закономерности его колебаний.
7. Какие упражнения были выполнены вами с физическим маятником?
8. Дайте строгое определение крутильного маятника и опишите закономерности его колебаний.
9. Какие упражнения были выполнены вами с крутильным маятником?
10. Исходя из графика T= f(l) для физического маятника, определите при каком отношении (l/d) период колебаний стержня минимальный.
Отчет о выполнении лабораторной работы № 1
«Изучение колебательного движения»,
выполненной студент …...... курса, …...... Ф. И. …........
группа …. «…»…………. 200…г.
Цель работы: ……………………………………………………………………………………
Часть I. Математический маятник
Задание 1. Проверка влияния массы математического маятника на его период
колебаний
Длина маятника l =…м.
Первоначальное отклонение j =…
Таблица 1.1.
| № п/п | m, кг | N | t,с | T,с |
| 1 | ||||
| 2 | ||||
| 3 |
Вывод: …………………………………………………………………………………………….
Задание 2. Изучение зависимости периода колебаний математического маятника
от его длины
Первоначальное отклонение j =…
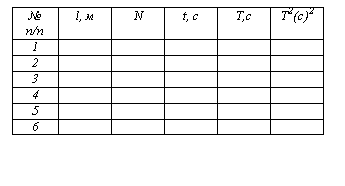 Таблица 1.2.
Таблица 1.2.
График зависимости T2=f(l)
Таблица 1.3. МНКОбозначения: l = x , T2 = y
| № п/п | xi |
|
| yi |
|
|
| |||||
| 1 |
|
|
|
|
|
|
| |||||
| 2 |
|
|
|
|
|
|
| |||||
| 3 |
|
|
|
|
|
|
| |||||
|
| ||||||||||||
|
|
| S = | S = |
| S = | S = | S = | |||||
Коэффициенты: ![]() = … ,
= … , ![]() =
=
Уравнение прямой: (T2) = …×l + …
Вычисление погрешностей измерений
![]() = … ,
= … , ![]() = … ,
= … , ![]() = … .
= … .
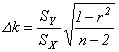 =…,
=…, ![]()
Контрольное задание. Определение ускорения свободного падения
k =…. g = 4p2/k=…. g =…±… м/с2 , dg =… %
Выводы: …………………………………………………………………………………………..
Часть II. Физический маятник
Задание 1. Изучение зависимости периода колебаний физического маятника от его
момента инерции и расстояния между осью качаний и центром тяжести
маятника
Первоначальное отклонение j =…
Таблица 2.1
| № п/п | l , м | N | t , c | T , c | l2, c2 | T2l , c2×м |
| 1 |
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
| И т. д. | ||||||
График зависимости T = f(l). График зависимости T2l =f(l2)
Выводы: ……………………………………………………………………………………………
Контрольное задание. Определение ускорения свободного падения и длины стержня
![]()
Выводы: …………………………………………………………………………………………..
Задание 2. Определение моментов инерции тел различной формы методом
колебаний
Форма тела: ………….
Масса тела: m = … ± …. кг
Расстояние от центра тяжести до оси качания: l = … ± … м
Период колебаний тела: Т = …±… с
Измеренный момент инерции тела относительно оси качания: J = … кг×м2
Формула для расчета погрешности измеренного момента инерции и расчет погрешности: ………………………………………………………………………………………………………
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = … ± …. кг× м2 ; dJ = … %
Геометрические размеры тела (с погрешностями измерений): …………………………….
Вычисленный момент инерции тела относительно центра тяжести: J = … кг×м2
Вычисленный момент инерции тела относительно оси качания: J = … кг×м2
Формулы для расчета погрешностей вычисленных моментов инерции и расчет погрешностей: ……………………………………………………………………………………………….
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = … ± …. кг× м2 ; dJ = … %
Выводы: ……………………………………………………………………………………………
Часть III. Крутильный маятник
Задание 1. Определение зависимости периода колебаний крутильного маятника от
момента инерции груза
Таблица 3.1.
| № стерж. |
m, кг |
l, м |
J, кгм2 |
N |
t, c
|
T, с |
T2, с2 |
| 1 |
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
График зависимости T2 =f(J)
Вывод: ……………………………………………………………………………………………..
Задание 2. Определение модуля сдвига материала методом крутильных колебаний
Материал подвеса: ............
Диаметр проволоки: d = ... ± .... мм = (… ± …)´10-3 м
Длина подвеса: L = ... ± ... см = (… ± …) ´10-2 м
Угловой коэффициент наклона графика: k =(DT)2/DJ = …
Коэффициент упругости кручения проволоки: f = 4p2/k = ….
Модуль сдвига материала проволоки:
G = ... ± ... Н/м2, dG = ... %
Выводы: .....................................................................................................................................…..
Задание 3. Определение моментов инерции тел методом крутильных колебаний
Форма тела: ……….
Масса тела: m = … ± …. кг
Коэффициент упругости кручения проволоки: f = ….
Период колебаний тела: Т = …±… с
Измеренный момент инерции тела относительно центра тяжести: J = … кг×м2
Формула для расчета погрешности измеренного момента инерции и расчет погрешностей: ……………………………………………………………………………………………….
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = … ± …. кг× м2 ; dJ = … %
Геометрические размеры тела (с погрешностями измерений): …………………………….
Вычисленный момент инерции тела относительно центра тяжести: J = … кг×м2
Формула для расчета погрешности вычисленного момента инерции и расчет погрешностей: ……………………………………………………………………………………………….
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = … ± …. кг× м2 ; dJ = … %
Выводы……………………………………………………………………………………………..
| |||
Цель работы
Углубить теоретические представления о механизмах возникновения внутреннего трения. Освоить методы измерения вязкости жидкостей и газов.
Похожие работы
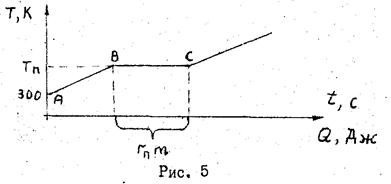
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... случайность, спонтанность непредсказуемость развития процесса (своего рода физический экзистенциализм), и в силу этого он далек от парадигмы абсолютности. Рассмотрим уровневый подход на примере энергии. Сегодня основные виды энергии в физике рассматриваются по парам: потенциальная – кинетическая, электрическая – магнитная, тепловая – механическая, причем каждая пара рассматривается автономно, ...
... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...
... . Фронт волны. Интерференция волн. Принцип Гюйгенса. Дифракция волн. Уравнение бегущей волны. Стоячие волны. Звуковые волны. Скорость звука. Громкость и высота звука. II. Молекулярная физика и термодинамика II.1. Основы молекулярно-кинетической теории Основные положения молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Массы и размеры молекул. Моль вещества. ...



0 комментариев