Исследование зависимости ускорения от силы при постоянной массе
Исследование зависимости ускорения от массы при постоянной силе
Экспериментальная установка
Зависимость углового ускорения e от действующего момента
Зависимость углового ускорения от момента действующих сил при J = const
Зависимость углового ускорения от момента инерции при M = const
Теоретическая часть
Теоретическая часть
Теоретическая часть
Теоретическая часть
Движение твердого тела в жидкости
Исходя из формулы р = nkT , вычислить концентрацию п молекул воздуха при нормальных условиях (k - постоянная Больцмана)
Эффективный диаметр молекул воздуха: d = … м
Навигация
Теоретическая часть
Физика: механика и термодинамика
67410
знаков
17
таблиц
19
изображений
1.1. Теоретическая часть
Маятник – тело, совершающее колебательное движение под действием упругой или подобной ей, «квазиупругой» силы. Простейший маятник – массивный груз на подвесе, находящийся в поле силы тяжести. Если подвес нерастяжим, размеры груза пренебрежимо малы по сравнению с длиной подвеса и масса нити пренебрежимо мала по сравнению с массой груза, то груз можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l от точки подвеса О. Такой маятник называется математическим.
На груз действуют силы: натяжения нити 
и тяжести 
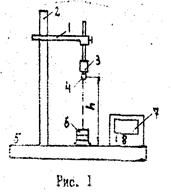
, которые в положении равновесия (точка С, рис.1) компенсируют друг друга 
. Для возбуждения колебаний маятник выводят из положения равновесия, например, в точку С`. Теперь на него действует сила 
, направленная к положению равновесия и пропорциональная смещению, маятник обладает избыточной потенциальной энергией mgh по отношению к положению равновесия. Эта энергия обуславливает колебание, происходящее по дуге окружности и описываемое основным уравнением динамики вращательного движения
, (1)
где 
- результирующий вращающий момент, модуль этого вектора равен 
; 
- угловое ускорение, J = ml2 – момент инерции груза относительно оси ОО¢, проходящей через точку подвеса О, перпендикулярно плоскости колебаний (плоскости чертежа).
Дифференциальное уравнение колебаний математического маятника в отсутствии сил сопротивления имеет вид
,
(2)
откуда получаем
(3)
Для достаточно малых углов (j<5-6°) sinj»j (в радианах), тогда
,
(4)
где 
.
Уравнение (4) представляет собой однородное дифференциальное уравнение второго порядка. Его решением является функция
, (5)
где j0 – амплитуда, a0 – начальная фаза. В этом можно убедиться, подставив (5) в (4).
Из (5) следует, что угол отклонения маятника из положения равновесия изменяется по гармоническому закону. Величина 
является циклической частотой собственных колебаний маятника, тогда величина
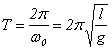(6)
- период колебаний математического маятника.1
Из выражения (6) следуют три закона колебаний математического маятника:
При малых углах отклонения (sinj»j или j<60) и в отсутствие сторонних сил
1. период колебаний не зависит от массы маятника;
2. период колебаний не зависит от амплитуды;
3. период колебаний определяется формулой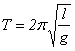 
.
Две из этих закономерностей подлежат проверке в данной работе.
1.2. Экспериментальная часть
Используемый в работе маятник представляет собой модель математического маятника - груз, подвешенный на тонкой нити. В работе используются не менее трех грузов, размеры которых значительно меньше длины нити (примерно как 1:50) и которые существенно отличаются по массе (примерно как 1:2:4), но близки по форме и размерам, чтобы силы сопротивления, возникающие при их движении, были примерно одинаковыми. Следует помнить, что длина маятника – это расстояние от точки подвеса до центра массы груза. Начальный угол отклонения маятника из положения равновесия не следует брать больше, чем 10-15°.
Задание 1. Проверка влияния массы математического
маятника на период его колебаний
1. Закрепив тело на подвесе, измеряют время 10 – 20 полных колебаний при возможно большей длине маятника. Повторяют измерения для других грузов. Данные заносят в таблицу 1.1 отчета.
2. Вычисляют период колебаний с точностью до 0,001 секунды.
3. Вычисляют оценочно относительную инструментальную погрешность измерений d.
4. Сравнивают периоды колебаний. Если различие в периоде колебаний не превышает 1% (приблизительно 0,01 с), то можно сделать вывод о практической независимости периода колебаний математического маятника от его массы.
Задание 2. Изучение зависимости периода колебаний
математического маятника от его длины
1. Подвешивают на нити стальной шарик. Длину подвеса изменяют с таким шагом, чтобы получить с данной нитью 5-6 экспериментальных точек. Число колебаний в каждом опыте 10-15. Угол отклонения маятника из положения равновесия не должен превышать 5-6°. Полученные данные заносят в таблицу 1.2 отчета.
2. Зависимость Т=f(l) нелинейная. Поэтому для удобства экспериментальной проверки эту зависимость следует линеаризировать. Можно, например, построить график зависимости квадрата периода колебаний от длины маятника Т2=f(l). Если экспериментальные точки ложатся на прямую с небольшим разбросом, то можно сделать вывод о выполнении формулы (6) и следовательно, одного из законов математического маятника. Если разброс велик, то следует повторить всю серию измерений.
Контрольное задание. Определение ускорения свободного падения.
С помощью полученного графика можно определить ускорение свободного падения. Предварительно следует получить точное уравнение экспериментальной прямой. Для этого применяют метод наименьших квадратов (МНК) и определяют угловой коэффициент прямой, т.е.
k=DT2/Dl = 4p2/g , откуда g=4p2/k.
Определите из графика k =DT2/Dl и вычислите ускорение свободного падения.
По формулам МНК определите погрешность измерения g.
Часть II. Физический маятник
Похожие работы
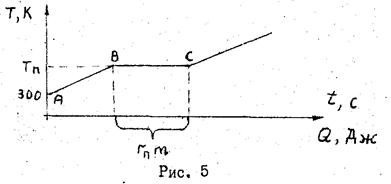
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... случайность, спонтанность непредсказуемость развития процесса (своего рода физический экзистенциализм), и в силу этого он далек от парадигмы абсолютности. Рассмотрим уровневый подход на примере энергии. Сегодня основные виды энергии в физике рассматриваются по парам: потенциальная – кинетическая, электрическая – магнитная, тепловая – механическая, причем каждая пара рассматривается автономно, ...
... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...
... . Фронт волны. Интерференция волн. Принцип Гюйгенса. Дифракция волн. Уравнение бегущей волны. Стоячие волны. Звуковые волны. Скорость звука. Громкость и высота звука. II. Молекулярная физика и термодинамика II.1. Основы молекулярно-кинетической теории Основные положения молекулярно-кинетической теории и их опытное обоснование. Броуновское движение. Массы и размеры молекул. Моль вещества. ...
0 комментариев