Теорема Шеннона

1.3 Теорема Шеннона

Любая булева функция  представима в виде разложе-ния Шеннона:

где ,  - первичные термы.

Пример.

Пусть п = 4, k = 2. Тогда разложение Шеннона будет иметь вид

Следствие.

Предельное разложение Шеннона (k = n) булевой функции  имеет вид

.

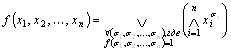Предельное разложение Шеннона булевой функции  является ее СДНФ.

В алгебре логики справедлив принцип двойственности. Согласно этому принципу, будем иметь следующие двойственные разложения Шеннона булевой функции :

по k переменным

двойственное предельное разложение

.

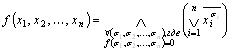Двойственное предельное разложение Шеннона булевой функции  является ее СКНФ.

2 Булевы функции двух переменных

Рассмотрим простой бинарный элемент – выключатель, который имеет два состояния. Если данный выключатель контролируется входной переменной х,то говорят, что он выключен (открыт) при х = 0 и включен (закрыт) при х = 1, как показано на рис. 1:

х = 0 х = 1

Рис. 1 - Два состояния выключателя

Будем использовать следующее графическое обозначение для представления таких выключателей:

х

Рис. 2 - Графическое обозначение выключателя

Рассмотрим соединения лампы с источником питания, представленные следующими схемами:

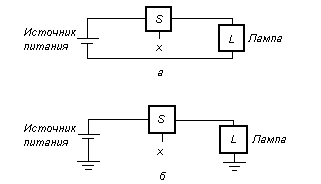
Рис. 3 - Лампа, управляемая выключателем: а – простое соединение с батареей; б – использование заземления, как обратной связи

Используя условное обозначение L, можно описать состояние лампы как функции входной переменной. Если лампа светится, то L = 1. Если лампа не светится, то L = 0. Поскольку L = 1 при х = 1, L = 0 при х = 0, то можно говорить, что L(х) = х – логическая функция, х – логическая переменная. Это простое логическое выражение описывает выход как функцию от входа.

2.1 Булевы функции от двух переменных

Рассмотрим теперь возможность использования двух выключателей для управления состоянием лампы. Пусть х₁ и х₂ – управляющие переменные (входы) для этих выключателей. Выключатели могут быть соединены последовательно или параллельно, как показано на рис. 4:

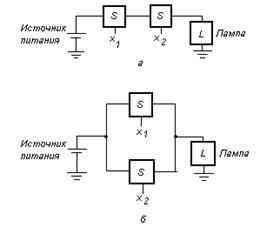
Рис. 4 - Две основные функции: а – последовательное соединение (функция логического умножения AND); б – параллельное соединение (функция логического сложения OR)

2.2 Последовательное соединение двух выключателей

При последовательном соединении лампа будет светиться только, если оба выключателя включены (одновременно). Это поведение может быть описано выражением: , где L = 1 при х₁ = х₂ = 1,

L = 0 в противном случае.

Символ  называется AND-оператором. Говорят, что схема на рис. 3.4,а реализует логическую AND-функцию (логическое умножение).

2.3 Параллельное соединение двух выключателей

При параллельном соединении двух выключателей лампа будет гореть, если выключатели х₁ и х₂ включены. Лампа также будет гореть, если оба выключателя включены (одновременно). Лампа не будет гореть только, если оба выключателя открыты (разомкнуты, выключены). Это поведение может быть описано как:

, где L = 1 при х₁ = 1 или х₂ = 1, или х₁ = х₂ = 1; L = 0 при х₁ = х₂ = 0.

Символ  называется OR-оператором. Говорят, что схема на рис. 4,б реализует логическую OR-функцию (логическое сложение).

В приведенных выше выражениях для AND и OR реализует результат (выход)  есть логическая функция с двумя входными переменными. Функции AND и OR являются двумя наиболее важными логическими функциями. Вместе с некоторыми другими простыми функциями они могут быть использованы как составные части (строительные блоки) для реализации логических схем.

Например, на рис. 5 показано, как три выключателя могут быть использованы для управления лампой в более сложном случае. Такое последовательно-параллельное соединение выключателей реализует логическую функцию:

.

Лампа горит, если х₃ = 1 и одновременно равны 1 либо х₁, либо х₂ (х₁ = 1 или х₂ = 1)

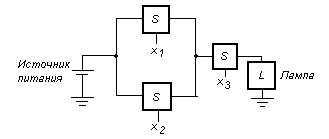
Рис. 5 - Последовательно-параллельное соединение выключателей