Навигация
Инверсия
2.4 Инверсия
Пусть лампа подсоединяется к источнику питания так, как показано на рис. 6:
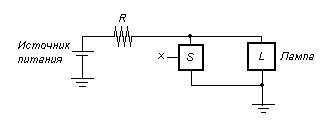
Рис. 6 - Инвертирующая схема
В этом случае выключатель соединяется параллельно с лампой. Лампа будет гореть, когда выключатель выключен. Формально такое функци- ональное поведение выражается: ![]() , где L = 1 при х = 0 и L = 0 при х = 1. Значение этой функции обратно значению входной переменной.
, где L = 1 при х = 0 и L = 0 при х = 1. Значение этой функции обратно значению входной переменной.
Вместо слова инверсия существует более общий термин отрицание.
Таким образом, ![]() есть отрицание х:
есть отрицание х: ![]() . Символ ¯ называют NOT-оператором.
. Символ ¯ называют NOT-оператором.
Количество логических функций в зависимости от числа переменных равно ![]() . Булевых функций одной переменной – четыре:
. Булевых функций одной переменной – четыре:
| x | f0 | f1 | f2 | f3 |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Индекс I функциональной переменной fi, I = 0, 1, 2, 3, равен десятичному эквивалентному набору значений этой функции, читаемому сверху вниз.
Функции f0(x) и f3(x) – константы 0 и 1 соответственно. Их значения не зависят от значения переменной х. Функция f1(x) “ повторяет “ х: f1(x) = x.
Функция f2(x) называется отрицанием х (или функцией НЕ) и обозначается ![]() , т.е. f2(x) =
, т.е. f2(x) = ![]() . Ее значение противоположно значению х.
. Ее значение противоположно значению х.
Булевых функций двух переменных – шестнадцать:
| x1 | x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Индекс I функциональной переменной fi, I = 0, 1, 2, …, 15, равен десятичному эквивалентному набору значений этой функции, читаемому сверху вниз. Приведем эти булевы функции:
![]() - константа ноль;
- константа ноль;
![]() - конъюнкция;
- конъюнкция;
![]() х1 –|→
х1 –|→ ![]() - левая коимпликация (читается «не если х1, то х2», префикс ко – от лат. conversus – обратный);
- левая коимпликация (читается «не если х1, то х2», префикс ко – от лат. conversus – обратный);
![]() ;
;
![]() х1 ←|– х2 - правая коимпликация;
х1 ←|– х2 - правая коимпликация;
![]() ;
;
![]() - сложение по модулю два или функция неравнозначности, неэквивалентности;
- сложение по модулю два или функция неравнозначности, неэквивалентности;
![]() - дизъюнкция;
- дизъюнкция;
![]() х1 ◦ х2 = х1 ↓ х2 - функция Вебба (Пирса);
х1 ◦ х2 = х1 ↓ х2 - функция Вебба (Пирса);
![]() х1 ~ х2 – функция эквивалентности, равнозначности;
х1 ~ х2 – функция эквивалентности, равнозначности;
![]() - отрицание х2;
- отрицание х2;
![]() - правая импликация (читается « если х2, то х1»);
- правая импликация (читается « если х2, то х1»);
![]() - отрицание х1;
- отрицание х1;
![]() - левая импликация (читается «если х1, то х2»);
- левая импликация (читается «если х1, то х2»);
![]() - функция Шеффера;
- функция Шеффера;
![]() - константа единица.
- константа единица.
Похожие работы
... утверждают или отрицают какие-либо отношения между объектами и явлениями реальной действительности. 3.Математическая логика и «Здравый смысл» в XXI веке. Логика - не только сугубо математическая, но также и философская наука. В XX веке эти две взаимосвязанные ипостаси логики оказались разведенными в разные стороны. С одной стороны логика понимается как наука о законах правильного мышления, ...
... занимательности. Упражнения однотипны. Поэтому просто необходимо дополнять данные в учебнике упражнения дополнительными заданиями развивающего характера. Глава II. Методика изучения элементов алгебры и математической логики. § 1. Методика изучения числовых выражений, выражений с переменными, числовых равенств и неравенств, уравнений. Изучение числовых выражений, равенств и неравенств, а ...
... утверждение "Я никогда не пользуюсь методами математической логики". Очевидно, что они противоречат друг другу, однако они вполне могут оказаться одновременно ложными. Например, если вы специалист по математической логике, то вы должны часто пользоваться её методами, но вряд ли они нужны вам каждый день вашей жизни. Закон исключенного третьего предназначен для использовании в области точных наук, ...
... постулаты D (то есть аксиомы Ax Ì FÍ A* и дедуктивные средства P Ì Fn+1), то говорят о построении теории как формальной системы F.S. = <L, D> = <A, S, Ax, P>Þ <A, F, Ax, P>. Другим подходом к построению математической логике является - содержательный, то есть неформальный. В этом случае аксиомы и дедуктивные средства явным образом не определяются (то есть ...
0 комментариев