Навигация
Этап. Определение сокращенной ДНФ
1 этап. Определение сокращенной ДНФ.
По двоичным наборам запишем 0-кубы:
К 0 = {0011, 0100, 0101, 0111, 1001, 1011, 1100, 1101}.
Выполним их разбиение на подгруппы по количеству единиц:
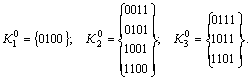
Строим К 1-кубы, сравнивая соседние подгруппы:
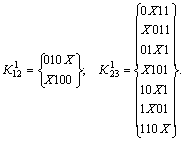
Выполним разбиение всех К 1-кубов в зависимости от положения независимой координаты Х:
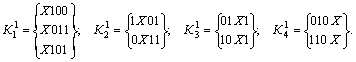
Выполним сравнение кубов внутри каждой подгруппы с целью построения К 2-кубов:
![]()
Поскольку они одинаковы, то ![]()
Записываем сокращенную ДНФ, в которую входят простые импликанты из К 1 (не вошедшие в К 2) и К 2:
![]()
2 этап. Определение тупиковой ДНФ.
Строим таблицу покрытий, в которую следует включать и те двоичные наборы, которые на любой итерации не участвовали ни разу в склеивании:
| Простые импликанты | Исходные термы |
| |||||||
| 0011 | 0100 | 0101 | 0111 | 1001 | 1011 | 1100 | 1101 |
| |
| 0 – 11 | * | * | |||||||
| - 011 | * | * | |||||||
| 01 – 1 | * | * | |||||||
| 10 – 1 | * | * | |||||||
| 1 – 01 | * | * | |||||||
| - 10 - | * | * | * | * | |||||
Определяя минимальное число строк, покрывающих все столбцы таблицы, находим тупиковую ДНФ:
![]()
Литература
1. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. – 311 с.
2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987. – 496 с.
3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988. – 480 с.
4. Сигорский В.П. Математический аппарат инженера. – М.: Техника, 1975. – 768 с.
5. Шапорев С.Д. Дискретная математика. – СПб., 2006. - 400 с.
6. Хаханов В.И., Чумаченко С.В. Дискретная математика. Конспект теоретического материала (электронная версия). ХНУРЭ, 2003.
7. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1979. – 272 с.
8. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: ФИЗМАТЛИТ, 2005. – 416 с.
Похожие работы
... утверждают или отрицают какие-либо отношения между объектами и явлениями реальной действительности. 3.Математическая логика и «Здравый смысл» в XXI веке. Логика - не только сугубо математическая, но также и философская наука. В XX веке эти две взаимосвязанные ипостаси логики оказались разведенными в разные стороны. С одной стороны логика понимается как наука о законах правильного мышления, ...
... занимательности. Упражнения однотипны. Поэтому просто необходимо дополнять данные в учебнике упражнения дополнительными заданиями развивающего характера. Глава II. Методика изучения элементов алгебры и математической логики. § 1. Методика изучения числовых выражений, выражений с переменными, числовых равенств и неравенств, уравнений. Изучение числовых выражений, равенств и неравенств, а ...
... утверждение "Я никогда не пользуюсь методами математической логики". Очевидно, что они противоречат друг другу, однако они вполне могут оказаться одновременно ложными. Например, если вы специалист по математической логике, то вы должны часто пользоваться её методами, но вряд ли они нужны вам каждый день вашей жизни. Закон исключенного третьего предназначен для использовании в области точных наук, ...
... постулаты D (то есть аксиомы Ax Ì FÍ A* и дедуктивные средства P Ì Fn+1), то говорят о построении теории как формальной системы F.S. = <L, D> = <A, S, Ax, P>Þ <A, F, Ax, P>. Другим подходом к построению математической логике является - содержательный, то есть неформальный. В этом случае аксиомы и дедуктивные средства явным образом не определяются (то есть ...
0 комментариев