Связь между связностью пространств

2.3. Связь между связностью пространств

и отображений

Пусть пространство Y = {*} – одноточечное. В этом случае отображение f : X→Y непрерывно и является связным (несвязным) тогда и только тогда, когда пространство Х связно (несвязно), т.к. трубки и слои над пространством Y совпадают со всем пространством Х.

Этот факт позволяет строить многочисленные примеры связных и несвязных отображений. Для этого достаточно взять связные и несвязные пространства и отображение их в одноточечные множества.

Пример. Рассмотрим отображение f : [-1;1] ® R, для которого f (х) = 0 при любом х Î [-1;1]. Отображение f связно тогда и только тогда, когда слой f ^–1(y) над точкой y = 0 связен. Но f ^–1(0) = [-1;1] – связное множество. Причём, понятия трубки и слоя над точкой y = 0 совпадают, поэтому отображение f является связным и послойно связным.

Если отображение f : [-1;1]  [2;3] ® R задано условием f (х) = 0 для любого х Î [-1;1]  [2;3], то оно несвязно (послойно несвязно) над точкой y = 0 в силу несвязности трубки (слоя) f ^–1(0) = [-1;1]   [2;3].

В рассмотренных примерах пространство Y является связным. Это условие и условие связности отображения f оказались необходимым и достаточным условием для связности пространства Х. Более того, имеет место

Теорема 2.4. Пусть сюръективное отображение f : X→Y непрерывно и связно. Пространство X является связным тогда и только тогда, когда пространство Y связное.

Доказательство. Необходимость. По теореме 1.5 (§1), если f : Х→Y непрерывное отображение, f (X) = Y и Х связно, то Y связно.

Достаточность. Пусть пространство Y связно. Предположим, что пространство Х несвязно. Тогда в Х найдутся такие непустые дизъюнктные открытые множества О₁ и О₂, что О₁  О₂ = Х. Допустим, что найдётся точка y Î . Тогда в любой окрестности слоя f ^–1(y) содержаться как точки множества О₁, так и точки множества О₂. С другой стороны, f ^–1(y) Ì f ^–1(U), где трубка f ^–1(U) является связным множеством (в силу связности отображения f над точкой y) и должна содержаться либо в О₁, либо в О₂ (по теореме 1.4). Получили противоречие. Следовательно,

 = Æ,

т.е. и  – непустые дизъюнктные замкнутые множества. Но f (О₁)  f (О₂) = Y, значит,

 = f (О₁) и  = f (О₂),

т.е. эти множества открыто-замкнутые. Это противоречит связности пространства Y.

Таким образом, предположение о несвязности топологического пространства Х неверно, а верно то, что требуется доказать.

Другой связи между связностью пространств и связностью отображений может и не быть.

Рис. 2.

Рис. 1.

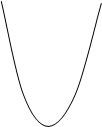
Примеры. Пусть отображение f : X→Y непрерывно. Если пространство Х связно, то и его образ f (X) связен, но отображение f не обязано быть связным. А именно, пусть f : R ® [0; + ¥], и f (х) = х ² для любого х Î R (рис. 1). Расмотрим произвольную точку y Î (0; + ¥). Пусть окрестностью точки y является любой интервал U = (a; b) Í (0; + ¥), содержащий эту точку. Тогда трубка

f ^–1(U) = 

распадается на два непустых непересекающихся открытых в R множества, т.е. f ^–1(U) – несвязное множество. Таким образом, отображение f несвязно по определению.

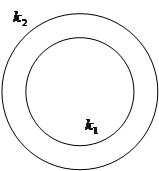
Можно привести ещё пример такого рода. Пусть Oxy – прямоугольная декартова система координат. Рассмотрим кольцо ω с центром в начале координат и радиусами r = a, R = b (рис. 2). Пусть pr_X : ω → [– b; b] – проекция этого кольца на ось Ox, где pr_X (x; y) = х Î [– b; b] для любой точки (x; y) Î ω. Возьмём произвольную точку х Î (– a; a) Ì [– b; b]. Для любой окрестности U Ì (– a; a) точки х трубка  является несвязной, т.к. состоит из двух частей A и B (рис. 2). Таким образом, проекция pr_X  – является несвязным отображением.

Рис. 4.

Рис. 3.

Может быть и наоборот, отображение f связное, а пространства X и Y – несвязные.

Пусть, например, отображение f : R \ {0} ® R \ {0} задано формулой f (х) =  для любого х Î R \ {0} (рис. 3). Возьмём произвольную точку y Î R \ {0}. Для любой окрестности Oy Ì R \ {0} точки y найдётся связная окрестность U Í (0; + ¥) (или U Í (– ¥; 0)), трубка f ^–1(U)  над которой связна (т.к. f ^–1(U) содержит часть ветви гиперболы или всю ветвь, которая связна и даже линейно связна).

Пусть Х = [0; 1], Y = [0; 1]  [2; 3]. Рассмотрим проекцию : X ´ Y ® Y (рис. 4), где pr_Y (x; y) = y Î Y для любой точки (x; y) Î X ´ Y. Множества X ´ Y  и Y являются несвязными, но проекция – связное отображение (в силу теоремы 2.7, которая будет доказана в пункте 2.4).

Рассмотрим другие примеры связных отображений, связаные с непрерывными числовыми функциями.

Теорема 2.6. Непрерывная функция f : [a; b] → R является связной тогда и только тогда, когда она монотонна, т.е. когда для любых точек х, х¢ Î [a; b], где х £ х¢, выполняется только одно из двух свойств: f (x) £ f (x¢ ) либо f (x) ³ f (x¢ ).

Доказательство. Необходимость. Функция f является отображением компактного множества в хаусдорфово пространство, поэтому она замкнута (в силу предложения 2.1). Тогда, по теореме 2.3, функция f является послойно связной.

Предположим, что f – не монотонна. Тогда найдутся такие точки х₁, х₂, х₃ Î [a; b] и х₁ <  х₂ <  х₃, для которых выполняется система неревенств:

.

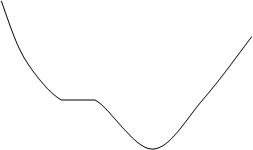
Положим f (x₁) = y₁, f (x₂) = y₂, f (x₃) = y₃ и y₃ ³ y₁ (или y₁ ³ y₃). Тогда слой f ^–1(y₃) является связным замкнутым подмножеством прямой y = y₃ (рис. 5), т.е. отрезком. По теореме о промежуточном значении функции, существует точка х¢ Î [x₁; x₂) и f (x¢ ) = y₃. В силу связности слоя f ^–1(y₃), отрезок [А ; В] (см. рис. 5) должен целиком лежать в слое f ^–1(y₃). Но точка (x₂; y₂), где x¢ < x₂ < x₃, не принадлежит прямой y = y₃, поэтому слой f ^–1(y₃) распадается на два непустых непересекающихся замкнутых в f ^–1(y₃) множества. Это противоречит послойной связности функции f. Следовательно, f – монотонна.

Достаточность. Предположим, что функция f не является связной. Следовательно,  f не является послойно связной (по теореме 2.3). Тогда существует такая точка y¢ Î R, что слой  f ^–1(y¢) – несвязен, т.е. f ^–1(y¢) = О₁  О₂, где О₁ и О₂ – непустые дизъюнктные замкнутые в f ^–1(y¢) множества (рис. 6). Следовательно, найдутся такие точки x₁ Î О₁, x₂ Î О₂ и точка х, где x₁ < x < x₂ и x Ï О₁, x Ï О₂, что

.

Но это противоречит условию монотонности функции f. Значит, функция f является связной. ÿ

Данная теорема утверждает, что связные функции, непрерывные на отрезке, – это либо невозрастающие, либо неубывающие функции.

Этот факт обобщается на случай интервала (a; b). Если связная функция f определена на R с конечным числом точек разрыва, то её монотонность в общем виде нарушается, но область определения можно разбить на конечное число промежутков, на каждом из которых функция f будет монотонной.