СОСТАВИМ СВОДНУЮ ТАБЛИЦУ ВЫЧИСЛЕНИЙ (табл. 14)

6.  СОСТАВИМ СВОДНУЮ ТАБЛИЦУ ВЫЧИСЛЕНИЙ (табл. 14)

Таблица 14

Параметры	Модель
	линейная	степенная
Коэффициент множественной корреляции	0,8235	0,8429
Коэффициент детерминации	0,6782	0,7106
F – критерий Фишера	7,375	8,592
Средняя относительная ошибка аппроксимации, %	3,53	3,42

В целом модели имеют примерно одинаковые характеристики. Но лучшей считается степенная модель, т.к значение коэффициента корреляции, индекса детерминации, F – критерия Фишера немного больше, а средняя относительная ошибка аппроксимации немного меньше, чем у линейной модели.

7.  НАЙДЕМ ЧАСТНЫЕ КОЭФФИЦИЕНТЫ ЭЛАСТИЧНОСТИ И β – КОЭФФИЦИЕНТЫ

Для нахождения частных коэффициентов эластичности составим частные уравнения регрессии, т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором х при закреплении других учитываемых во множественной регрессии на среднем уровне.

и т.д.

Результаты расчетов представлены в таблице 15.

Таблица 15

Вспомогательная таблица для вычисления частных коэффициентов эластичности

Y	X1	X2	Э(ух1)	Э(ух2)
3,0	1,1	0,4	0,524	-0,135
2,9	1,1	0,4	0,524	-0,135
3,0	1,2	0,7	0,545	-0,262
3,1	1,4	0,9	0,583	-0,364
3,2	1,4	0,9	0,583	-0,364
2,8	1,4	0,8	0,583	-0,311
2,9	1,3	0,8	0,565	-0,311
3,4	1,6	1,1	0,615	-0,484
3,5	1,3	0,4	0,565	-0,135
3,6	1,4	0,5	0,583	-0,174

Бета коэффициент рассчитываем по формуле:

 - среднее квадратическое отклонение.

Необходимые вычисления для расчета СКО представлены в таблице 9.

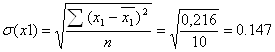
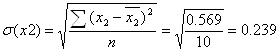
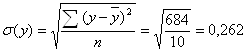
Если объем капиталовложений увеличить на величину своего СКО, т.е. 0,147 млн. руб., то выручка предприятия увеличится на 1,302 величины своего СКО, т.е. на 1,302 * 0,262 = 0,341 млн. руб.

Если основные производственные фонды увеличить на величину своего СКО, т.е. на 0,239 млн. руб., то выручка предприятия уменьшится на 1,068 своего СКО, т.е. на 1,068 * 0,262 = 0,280 млн. руб.

8.  ПО ЛИНЕЙНОЙ МОДЕЛИ РЕГРЕССИИ СДЕЛАЕМ ПРОГНОЗ НА СЛЕДУЮЩИЕ ДВА ГОДА показателя у (выручка), в зависимости от х₁ (объема капиталовложений) и х₂ (основных производственных фондов).

Прогнозные значения факторов можно получить, используя метод прогнозирования с помощью среднего абсолютного прироста:

,

где  - средний абсолютный прирост, рассчитываемый по формуле:

;

k – период упреждения;

n – количество наблюдений.

, тогда

Х_{1, 11} = 1,4 + 1 ∙ 0,0333 = 1,4333 (млн.руб.)

Х_{1, 12} = 1,4 + 2 ∙ 0,0333 = 1,4667(млн.руб.)

Х_{2, 11} = 0,5 + 1 ∙ 0,0111 = 0,5111

Х_{2, 12} = 0,5 + 2 ∙0,0111 = 0,5222

Составляем вектор прогнозных значений факторов:

.

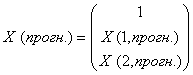
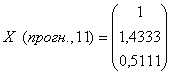
Вычислим точечные прогнозы поведения выручки предприятия на моменты времени t = 11 и t = 12. Для этого подставим прогнозные значения факторов в уравнение регрессии.

 (млн. руб.)

 (млн. руб.)

Для получения интервального прогноза  рассчитываем доверительные интервалы, используя величину отклонения от линии регрессии (U):

,

 

Операции с матрицами осуществим в среде Excel с помощью встроенных математических функций МУНОЖ и МОБР.

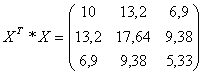
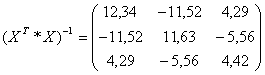
Среднее квадратическое отклонение расчетных значений от фактических:

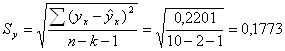
Коэффициент Стьюдента t_α для m = 10 – 2 – 1 = 7 степеней свободы и уровня значимости α = 0,05 равен 2,36.

U(11) = 0,1773 ∙ 2.36 ∙ 0,6161^0,5 = 0,329

U(11) = 0,1773 ∙ 2.36 ∙ 0.7481^0,5 = 0,362

Результаты вычислений представим в виде таблицы.

Таблица 16

Шаг	Точечный прогноз, млн. руб.	Нижняя граница, млн. руб.	Верхняя граница, млн. руб.
11	3,6121	3,2829	3,9412
12	3,6763	3,3136	4,0390

Список литературы:

1.  Доугерти К. Введение в эконометрику. – М.: Инфра – М, 2001. – 402 с.

2.  Катышев П. К., Пересецкий А. А. Сборник задач к начальному курсу эконометрики. – М.: Дело, 1999. – 72 с.

3.  Практикум по эконометрике: Учеб. пособие; Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2001. – 192 с.

4.  Тутыгин А.Г., Амбросевич М.А., Третьяков В.И. Эконометрика. Краткий курс лекций. Учебное пособие. – М.-Архангельск, Издательский дом «Юпитер», 2004. – 54 с.

5.  Эконометрика: Учеб. пособие; Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2001. –245 с.