НАЙДЕМ ПАРАМЕТРЫ СТЕПЕННОЙ МОДЕЛИ РЕГРЕССИИ

6.  НАЙДЕМ ПАРАМЕТРЫ СТЕПЕННОЙ МОДЕЛИ РЕГРЕССИИ

Произведем линеаризацию переменных путем логарифмирования обеих частей уравнения.

Сделаем замену переменной Y = lg y, A = lg a, X = lg x. Тогда Y = A + b ∙ X – линейная модель парной регрессии. Можно применить МНК.

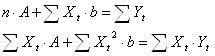
Необходимые расчеты представлены в таблице 5.

Построена степенная модель зависимости выручки предприятия «АВС» от объема капиталовложений:

Таблица 5

Вспомогательная таблица для расчетов показателей по степенной модель

t	y	x	Y = lg y	X = lg x	X2 = =lg x2	X*Y = lg x*lg y			A
1998	3,0	1,1	0,477	0,041	0,002	0,020	2,946	0,003	0,018
1999	2,9	1,1	0,462	0,041	0,002	0,019	2,946	0,002	0,016
2000	3,0	1,2	0,477	0,079	0,006	0,038	3,035	0,001	0,012
2001	3,1	1,4	0,491	0,146	0,021	0,072	3,200	0,010	0,032
2002	3,2	1,4	0,505	0,146	0,021	0,074	3,200	0,000	0,000
2003	2,8	1,4	0,447	0,146	0,021	0,065	3,200	0,160	0,143
2004	2,9	1,3	0,462	0,114	0,013	0,053	3,120	0,048	0,076
2005	3,4	1,6	0,531	0,204	0,042	0,108	3,350	0,002	0,015
2006	3,5	1,3	0,544	0,114	0,013	0,062	3,120	0,145	0,109
2007	3,6	1,4	0,556	0,146	0,021	0,081	3,200	0,160	0,111
Σ	31,4	13,2	4,955	1,178	0,163	0,592		0,532	0,531

7.  РАССЧИТАЕМ:

индекс корреляции:

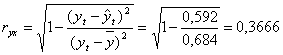
Связь между объемом капиталовложений и выручкой предприятия в степенной модели слабая.

коэффициент детерминации

Степенная модель всего на 13,44% детерминирует зависимость выручки предприятия от объема капиталовложений. 86,56% детерминации происходит под влиянием факторов не учтенных в модели.

F – критерий Фишера

Проверим значимость уравнения

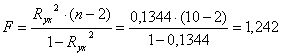
F(расч.) = 1,242 < F(табл.)= 5,318, т.е. уравнение степенной модели в целом можно считать статистически незначимым.

Среднюю относительную ошибку аппроксимации:

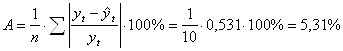
Ошибка меньше 7%, степенную модель можно считать точной.

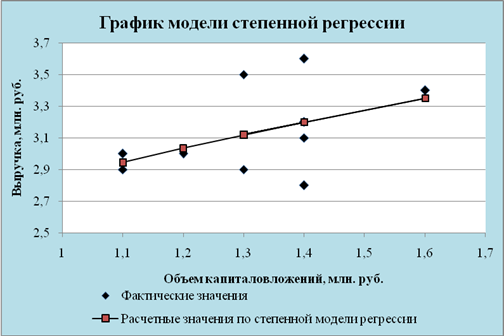
Рис. 4

8.  НАЙДЕМ ПАРАМЕТРЫ ПОКАЗАТЕЛЬНОЙ МОДЕЛИ РЕГРЕССИИ

Произведем линеаризацию переменных путем логарифмирования обеих частей уравнения.

Сделаем замену переменной Y = lg y, A = lg a, В = lg b. Тогда Y = A + B ∙ x – линейная модель парной регрессии. Можно применить МНК.

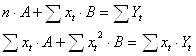
Необходимые расчеты представлены в таблице 6.

Таблица 6

Вспомогательная таблица для расчетов показателей по показательной модели

t	y	x	Y = lg y	x2	x*Y = x*lg y			A
1998	3,0	1,1	0,477	1,21	0,525	2,953	0,002	0,016
1999	2,9	1,1	0,462	1,21	0,509	2,953	0,003	0,018
2000	3,0	1,2	0,477	1,44	0,573	3,032	0,001	0,011
2001	3,1	1,4	0,491	1,96	0,688	3,196	0,009	0,031
2002	3,2	1,4	0,505	1,96	0,707	3,196	0,000	0,001
2003	2,8	1,4	0,447	1,96	0,626	3,196	0,157	0,141
2004	2,9	1,3	0,462	1,69	0,601	3,113	0,045	0,073
2005	3,4	1,6	0,531	2,56	0,850	3,369	0,001	0,009
2006	3,5	1,3	0,544	1,69	0,707	3,113	0,150	0,111
2007	3,6	1,4	0,556	1,96	0,779	3,196	0,163	0,112
Σ	31,4	13,2	4,955	17,640	6,565		0,531	0,524

Построена показательная модель зависимости выручки предприятия «АВС» от объема капиталовложений:

9.  РАССЧИТАЕМ:

индекс корреляции:

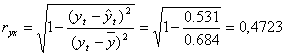
Связь между объемом капиталовложений и выручкой предприятия в степенной модели очень слабая.

коэффициент детерминации

В показательной модели изменение выручки на 22,30% обусловлено изменением объема капиталовложений, на 77,70% - влиянием факторов, не включенных в модель.

F – критерий Фишера

Проверим значимость уравнения

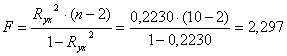
 F(расч.) = 2,297 < F(табл.) = 5,318, т.е. показательное уравнение в целом можно считать статистически незначимым.

Среднюю относительную ошибку аппроксимации:

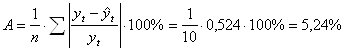
Ошибка меньше 7%, показательную модель можно считать точной.

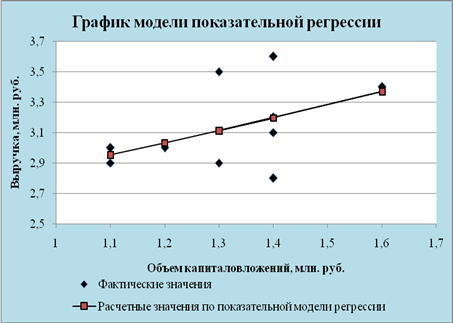
Рис. 5