Применение тригонометрической подстановки приучает учащихся к полноте аргументации введения подстановки для решения задач
Иррациональные уравнения
Рациональные уравнения
Показательные уравнения
Сколько решений имеет уравнение в зависимости от параметра
Исследованы теоретические основы возможности введения тригонометрической подстановки
Вспомнить теоретические основы введения тригонометрической подстановки
Навигация
Вспомнить теоретические основы введения тригонометрической подстановки
Применение тригонометрической подстановки для решения алгебраических задач
70384
знака
2
таблицы
19
изображений
1. Вспомнить теоретические основы введения тригонометрической подстановки.
2. Рассмотреть применение тригонометрической подстановки для решения иррациональных уравнений в случае, когда множество значений переменной 
ограничено.
3. Провести сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее.
Содержание:
1. Решить уравнение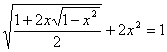 
.
2. Решите уравнение 
.
3. Решить уравнение 
.
4. Решить уравнение 
.
Домашнее задание:
1. Решить уравнение 
.
2. Решить уравнение 
.
3. Решить уравнение 
.
Литература: [3], [4], [12], [14], [23] – [25], [31], [32], [37] – [39], [43], [44], [47] – [51], [57].
Занятие №3
Тема: применение тригонометрической подстановки для решения систем уравнений.
Цели:
1. Рассмотреть применение тригонометрической подстановки для решения сложных, олимпиадных систем.
2. Провести сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее, где это возможно.
3. Привести пример системы, решить которую без тригонометрической подстановки не возможно.
Содержание:
1. Решить систему уравнений 
.
2. Решить систему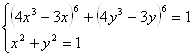 
.
3. Выяснить, сколько решений имеет система уравнений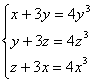 
.
4. При каких значениях параметра система имеет решение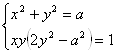 
.
Домашнее задание:
1. Решить систему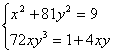 
.
2. Решить систему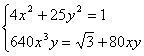 
.
3. Сколько решений имеет система уравнений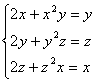 
.
Литература: [3], [6] – [8], [10], [12], [14], [18], [24], [30], [43].
Занятие №4
Тема: применение тригонометрической подстановки для решения задач на отыскание наибольшего и наименьшего значений функции.
Цели:
1. Вспомнить основные методы решения задач на отыскание наибольшего и наименьшего значений функции.
2. Показать, как метод тригонометрической подстановки применяется для решения задач на нахождение наибольшего и наименьшего значений функции.
3. Провести сравнительный анализ решения задач с помощью тригонометрической подстановки и без нее.
Содержание:
1. Найти наибольшее и наименьшее значение выражения
, если 
.
2. Найти наибольшее и наименьшее значение выражения
, если 
.
3. Среди всех решений системы найдите такие, при которых выражение 
принимает наибольшее значение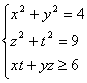 
.
4. Выяснить, при каких значениях параметра неравенство имеет решения 
.
Домашнее задание:
1. Найти наибольшее и наименьшее значение выражения 
, если 
.
2. Найти наибольшее и наименьшее значение выражения
, если 
.
3. Среди всех решений системы найти такие, при каждом из которых выражение 
принимает наименьшее значение
.
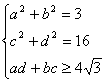Литература: [4], [14], [22], [24], [31], [42].
[1] Пример 2 пункта 1.2 Рациональные уравнения
[2] Здесь и далее процент подсчитывается от количества учащихся, выбравших указанный способ решения
Похожие работы
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
0 комментариев