Навигация
Расчёт коэффициентов передачи объекта
1.3 Расчёт коэффициентов передачи объекта
Коэффициент передачи объекта показывает, в какую сторону и в какой степени происходит изменение сигнала при прохождении его через объект, то есть усилительные свойства объекта.
Коэффициент передачи определяется как производная от выходной величины:
![]()
![]()
Расчет коэффициента передачи производим при 10%, 50% и 90% номинального режима, из таблицы данных находим максимальное и минимальное значения сигнала на выходе объекта
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решим алгебраические нелинейные уравнения, исследуем полученные корни и, подставив, нужный корень, получили коэффициенты передач.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таблица 4 – Результаты расчета коэффициентов передачи
| 10% | 50% | 90% | |
| y | 3,6 | 6 | 8,4 |
| k | 1,209 | 1,417 | 1,598 |
2 ПОСТРОЕНИЕ ДИНАМИЧЕСКОЙ МОДЕЛИ ОБЪЕКТА
Динамическая характеристика объекта нужна для построения его динамической математической модели, которая описывает поведение объекта во времени, начиная с момента подачи входного сигнала и до момента, когда все переходные процессы заканчиваются.
Динамические характеристики, в свою очередь, подразделяются на временные и частотные.
Временными характеристиками звена или системы называют изменение во времени значений выходной величины при поступлении на вход некоторого типового воздействия. Наиболее важной временной характеристикой является реакция системы на единичное, мгновенное, скачкообразное изменение значения входной величины, так как этот режим очень часто возникает в системах регулирования, как при включении, так и при изменении заданного значения регулируемой величины.
Таким образом, под временной характеристикой системы будем понимать процесс изменения выходной величины в функции времени при переходе системы из одного равновесного состояния в другое в результате поступления на вход системы единичного, ступенчатого воздействия.
Для получения динамической переходной характеристики объекта регулирования необходимо:
а) задаться рядом значений времени t;
б) зарегистрировать значение выходного сигнала Yi в заданные моменты t, в результате интенсивного экспериментирования. Эти данные сведены в таблицу 5.
Таблица 5 – Динамическая характеристика объекта регулирования
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 |
| Y | 0 | 0,1 | 0,5 | 0,7 | 0,82 | 0,91 | 0,975 | 0,99 | 1 |
Для получения аналитической зависимости, заданную таблично динамическую характеристику необходимо аппроксимировать выражением первого порядка. Затем по наименьшему значению суммы квадратов отклонений для характеристик без запаздывания и с запаздыванием нужно выбрать наиболее приближенную к экспериментальным данным динамическую характеристику.
Для статических объектов первого порядка без запаздывания будем иметь:
- дифференциальное уравнение
![]()
Т - постоянная времени, это время в течение которого выходная координата объекта достигла установившегося состояния, если бы изменялась с максимальной скоростью;
k - коэффициент передачи.
- передаточную функцию
![]()
- решение дифференциального уравнения
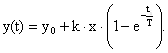
Для статических объектов первого порядка с запаздыванием будем иметь:
- дифференциальное уравнение
![]()
- передаточную функцию
![]()
- решение дифференциального уравнения
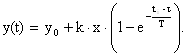
Для статических объектов N-го порядка без запаздывания, имеющих кратные (одинаковые корни), будем иметь:
- передаточную функцию
![]()
- решение дифференциального уравнения (переходный процесс)
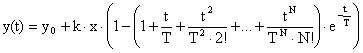
Для статических объектов N-го порядка с запаздыванием будем иметь:
- передаточную функцию
![]()
переходный процесс

Общий процесс решения поставленной задачи будет выглядеть следующим образом:
- составляем систему уравнений для всей совокупности экспериментальных точек. Для объектов высоких порядков систему предварительно линеаризуем посредством замены переменных и решения в каждой точке нелинейного уравнения для этой введенной дополнительной переменной;
- составляем систему уравнений для всей совокупности экспериментальных точек. Для объектов высоких порядков систему предварительно линеаризуем посредством замены переменных и решения в каждой точке нелинейного уравнения для этой введенной дополнительной переменной;
- полученную систему уравнений решаем матричным методом наименьших квадратов и находим неизвестные и T.
2.1 Динамическая модель объекта 1-го порядка без запаздывания
Расчёт вручную
Решением дифференциального уравнения будет являться сумма общего и частного решений:
![]()
Найдем Yобщ(t):
![]()
![]()
Найдем Yчаст(t):
![]()
Подставим:
![]()
Найдем постоянную С:
Y(0)=Y0
тогда
![]() ;
;
![]()
Подставим С:
![]()
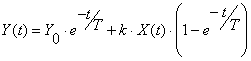
По таблице при t = 0, Y(0) = 0, тогда:
![]() , откуда
, откуда![]() и получим:
и получим:
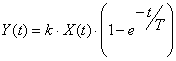
Где ![]() - установившееся значение, в нашем случае Yуст = Ymax.
- установившееся значение, в нашем случае Yуст = Ymax.
Найдем постоянную времени Т методом наименьших квадратов. Преобразуем выражение:
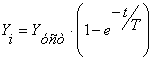
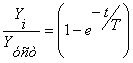
Прологарифмируем выражение:
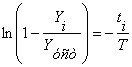
Обозначим
![]()
Рассчитаем ![]() для каждого момента времени ti и занесем в таблицу 6.
для каждого момента времени ti и занесем в таблицу 6.
Таблица 6 - Значения![]()
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
| 1 | 0.9 | 0.5 | 0.3 | 0.18 | 0.09 | 0.025 | 0.01 | 0 |
Далее составляем систему алгебраических уравнений:
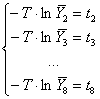
В систему не вошло уравнение для момента времени t9, так как ln0 не определен, и для момента времени t=0, так как в них![]() . Составляем матричное уравнение для:
. Составляем матричное уравнение для:
![]()
Составим матрицы:
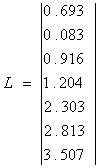
![]()
Находим произведение ![]() :
:
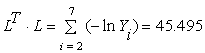
Находим произведение ![]() :
:
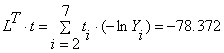
Окончательно найдем T:
![]()

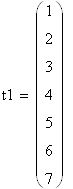
![]()
![]()
![]()
![]()
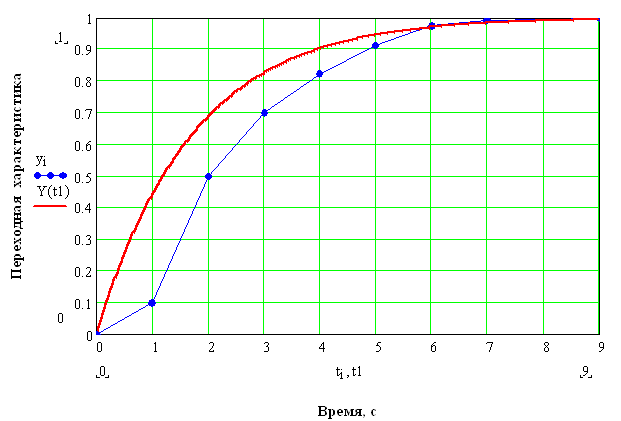
Рисунок 3 – График динамической модели объекта 1-го порядка без запаздывания

Расчёт вручную
Системой с запаздыванием называется система, в которой имеется звено, обладающее таким свойством, что реакция на его выходе отстает по времени на некоторую величину ![]() .
.
Объект первого порядка с запаздыванием можно описать уравнением вида:
Запишем решение дифференциального уравнения:
![]()
где
![]()
Найдем постоянную времени Т и время запаздывания ![]() методом наименьших квадратов. Преобразуем выражение:
методом наименьших квадратов. Преобразуем выражение:
![]()
Прологарифмируем выражение :
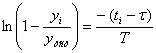
![]()
где ![]() , значение
, значение ![]() (таблица 6).
(таблица 6).
Составим систему алгебраических уравнений первого порядка, причем число уравнений равно числу состояний объекта в эксперименте, кроме точек ![]() , так как в них
, так как в них ![]() , а также точки и
, а также точки и![]() , так как в этой точке
, так как в этой точке ![]() не существует:
не существует:
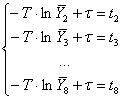
Составим матричное уравнение для решения системы:
![]()
где
![]() .
.
Составим матрицы L и t:
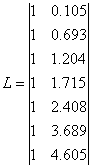
![]()
Найдем произведение ![]() :
:

Найдем произведение ![]() :
:

![]()
Найдем главный определитель:
![]()
Находим вспомогательные определители ![]() и
и ![]() , подставляя матрицу
, подставляя матрицу ![]() поочередно в первый и второй столбцы матрицы
поочередно в первый и второй столбцы матрицы ![]() соответственно:
соответственно:
![]()
![]()
Находим Т и t:
![]()
![]()
Расчёт в системе MathCAD
|
|
|
|
|
|
| - решение системы линейных алгебраических уравнений методом наименьших квадратов посредством обращения матрицы; |
|
|
|
|
| - время запаздывания; |
| - постоянная времени; |
![]()
![]()
![]()
![]()
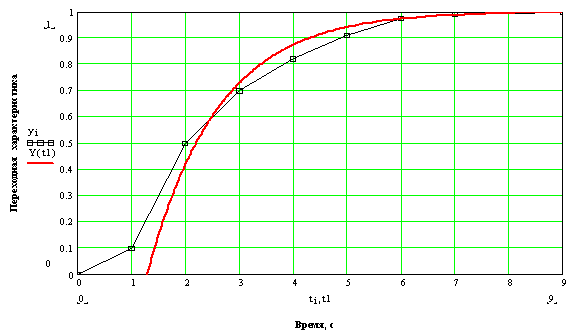
Рисунок 4 – График динамической модели объекта 1-го порядка с запаздыванием
| Таблицы исходных данных и результатов: |
![]()
|
|
|
|
|
|
|
|

![]()
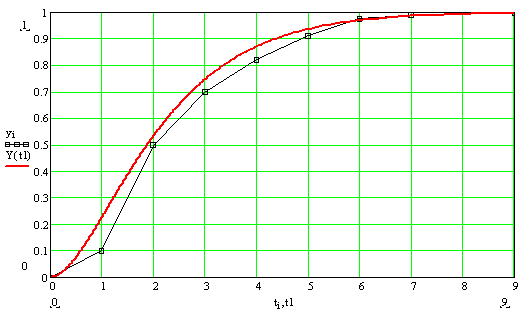
Рисунок 5 – График динамической модели объекта 2-го порядка без запаздывания
| Таблицы исходных данных и результатов: |
|
|
2.4 Динамическая модель объекта 2-го порядка с запаздыванием
|
|
|
|
|
|
| - длина вектора данных; |
|
|
|
|
|
|
| - задание границ адекватности исходных данных предполагаемой модели по значениям y1; |
|
|
|
|
| - нелинейное уравнение; |
|
|
| - решение нелинейного уравнения; |
|
|
| - вектор правых частей; |
|
|
|
|
|
|
|
|
|
|
| - вектор коэффициентов системы уравнений; |
- решение системы линейных алгебраических уравнений методом наименьших квадратов посредством обращения матрицы;
|
|
|
|
|
|
| - время запаздывания |
| - постоянная времени; |
|
|
|
|
|
|
|
|
|
|

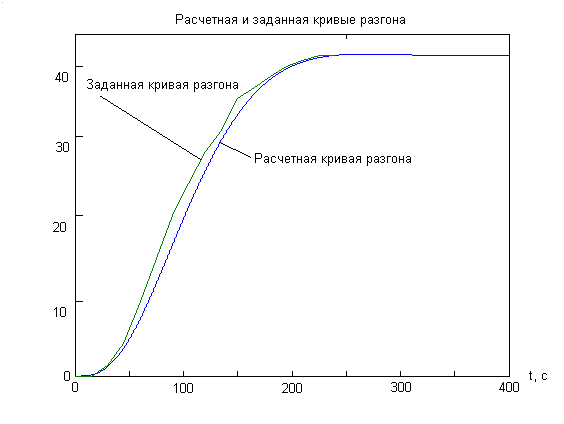
Рисунок 6 – График динамической модели объекта 2-го порядка с запаздыванием
| Таблицы исходных данных и результатов: |
![]()

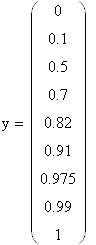
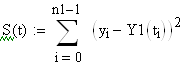
![]()
Таким образом, в результате расчета из четырёх моделей объекта выбрана модель второго порядка c запаздыванием, так как она наиболее точно отражает протекание переходных процессов и обеспечивает заданное качество регулирования. Это видно из расчетов, у этой модели сумма квадратов отклонений имеет наименьшее значение, чем у остальных объектов и также это видно из кривой переходного процесса.
Похожие работы
... , является то, что в замкнутой системе все физические величины, представляющие воздействие одного звена на другое, связаны в единую замкнутую цепь. Автоматические системы регулирования должны обеспечивать: - устойчивость системы при любых режимных ситуациях объекта; - минимальное время регулирования; - минимальные динамические и статические отклонения регулируемой величины, не выходящие ...
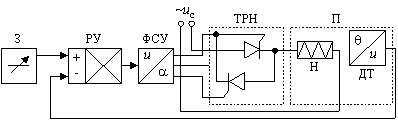
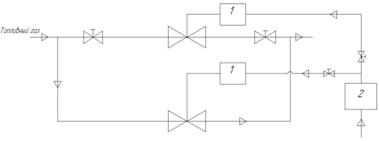
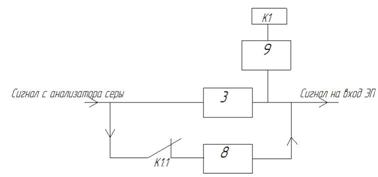
... , поддерживало температуру на нужном уровне. Установка требуемой температуры осуществляется с помощью задатчика (З). 1.2 Описание структурной схемы Рис. 2. Структурная схема автоматической системы регулирования температуры Входным сигналом системы является напряжение Uз, оно сравнивается с напряжением Uд ≈ Θ, которое действует на выходе датчика. Если Uз ≠ Uд, то ...
... на основе правил Госгортехнадзора с учетом местных условий и особенностей оборудования. Котел должен быть оборудован необходимым количеством контрольно-измерительных приборов, автоматической системой регулирования важнейших параметров котла, защитными устройствами, блокировкой и сигнализацией. Режимы работы котла должны соответствовать режимной карте, в которой указываются рекомендуемые ...
... системой: время наработки на отказ системы увеличилось на 2,73%. Вывод В ходе курсовой работы было произведено техническое обеспечение автоматической системы регулирования качества стабильного гидрогенизата. Были выбраны средства контроля и регулирования и обоснован их выбор. Был произведен расчет надежности контура регулирования, и предложена схема для резервирования самого ненадежного ...
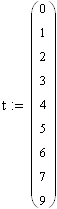
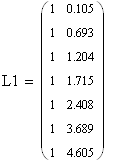
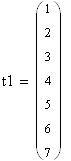


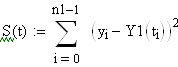
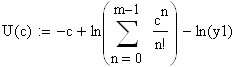
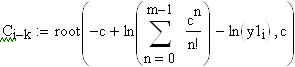


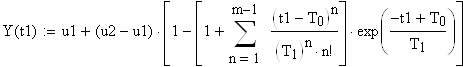
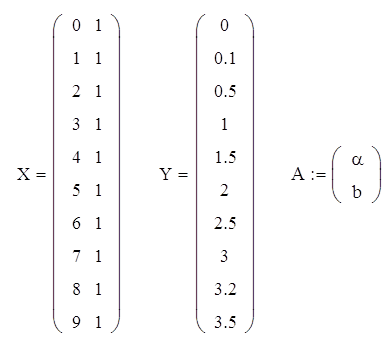
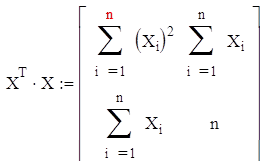
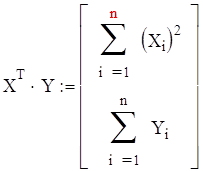
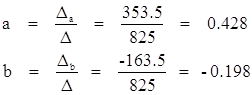
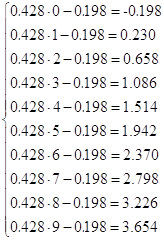
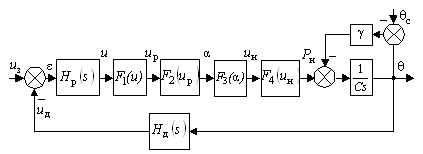
0 комментариев