Расчёт коэффициентов передачи объекта
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ОБЪЕКТА
Расчёт частотных характеристик в системе MathCAD
Расчет расширенных частотных характеристик объекта
ВЫБОР И РАСЧЕТ ПАРАМЕТРОВ НАСТРОЙКИ РЕГУЛЯТОРОВ
ПИ – регулятор
ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Замкнутая система с И – регулятором
Замкнутая система с П – регулятором по возмущению
ОЦЕНКА КАЧЕСТВА РАБОТЫ САУ
Навигация
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
Линейные автоматические системы регулирования
61629
знаков
361
таблица
80
изображений
3 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
3.1 Приведение к нормальной системе дифференциальных уравненийПусть имеем передаточную функцию в виде степенного полинома, который необходимо представить в обычной форме. В таком виде обычно формируется математическая модель объекта по результатам исследования. Передаточная функция представляет собой отношение выходной величины к входной величине, и она выбирается по минимальному среднеквадратическому отклонению от экспериментальных данных динамических характеристик. В нашем случае это передаточная функция динамической характеристики второго порядка с запаздыванием:
Где:
Разложим звено запаздывания в степенной ряд в виде отношения полиномов:
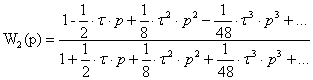
Тогда перемножая, получим:
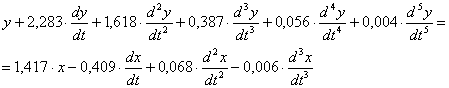
Получили дифференциальное уравнение. Приведем к нормальной системе дифференциальных уравнений методом формального интегрирования.
Получили нормальную систему дифференциальных уравнений, разрешённую относительно первой производной:
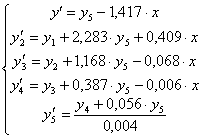
Неизвестную величину 
найдём из соотношения:
Где k - коэффициент передачи при 50% мощности от номинального режима;
- максимальное значение 
экспериментальных данных.
Подставив в полученную систему получим:
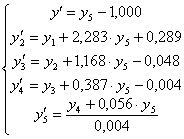
В результате решения получается матрица чисел, содержащая столбец точек независимой переменной (в нашем случае - времени) и столбцы соответствующих значений функций, определенных системой уравнений и вычисленных в этих точках.
3.2 Решение нормальной системы уравнений методом Рунге – Кутта, с постоянным шагом|
|
| - Вектор начальных условий; |
|
|
|
|
| - Количество точек; |
| - Вектор правых частей исходной системы дифференциальных уравнений в нормальной форме; |
|
|
| - Обращение к процедуре rkfixed |
|
|
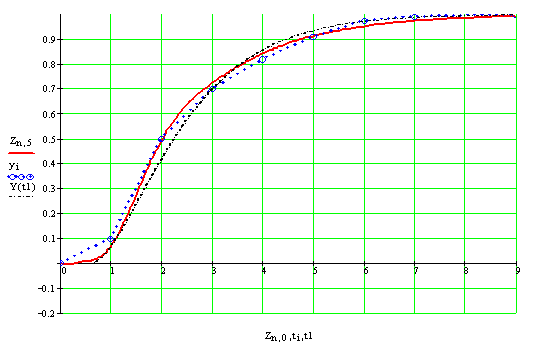
Время, с
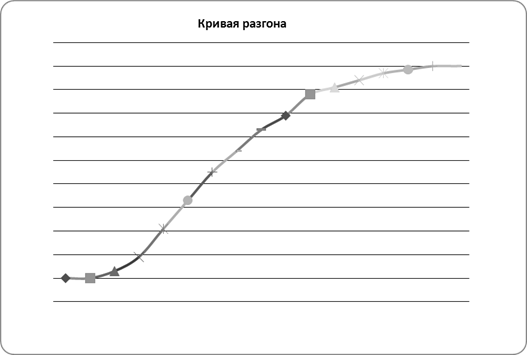
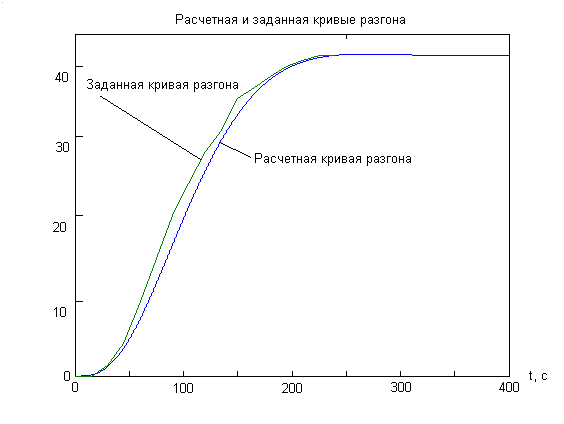
Рисунок 7 - График переходного процесса
На рисунке:
– исходные данные; Y(t1) – полином второго порядка с запаздыванием.
Похожие работы
... , является то, что в замкнутой системе все физические величины, представляющие воздействие одного звена на другое, связаны в единую замкнутую цепь. Автоматические системы регулирования должны обеспечивать: - устойчивость системы при любых режимных ситуациях объекта; - минимальное время регулирования; - минимальные динамические и статические отклонения регулируемой величины, не выходящие ...
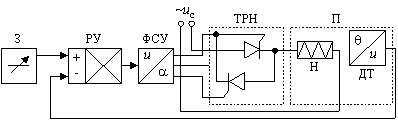
... , поддерживало температуру на нужном уровне. Установка требуемой температуры осуществляется с помощью задатчика (З). 1.2 Описание структурной схемы Рис. 2. Структурная схема автоматической системы регулирования температуры Входным сигналом системы является напряжение Uз, оно сравнивается с напряжением Uд ≈ Θ, которое действует на выходе датчика. Если Uз ≠ Uд, то ...
... на основе правил Госгортехнадзора с учетом местных условий и особенностей оборудования. Котел должен быть оборудован необходимым количеством контрольно-измерительных приборов, автоматической системой регулирования важнейших параметров котла, защитными устройствами, блокировкой и сигнализацией. Режимы работы котла должны соответствовать режимной карте, в которой указываются рекомендуемые ...
... системой: время наработки на отказ системы увеличилось на 2,73%. Вывод В ходе курсовой работы было произведено техническое обеспечение автоматической системы регулирования качества стабильного гидрогенизата. Были выбраны средства контроля и регулирования и обоснован их выбор. Был произведен расчет надежности контура регулирования, и предложена схема для резервирования самого ненадежного ...
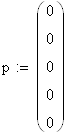
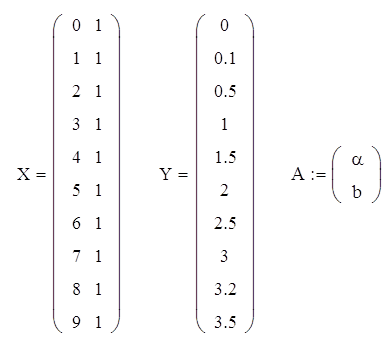
0 комментариев