Навигация
Замкнутая система с П – регулятором по возмущению
7.5.1 Замкнутая система с П – регулятором по возмущению
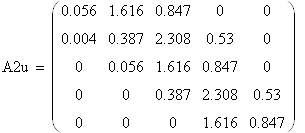
Составим вектор коэффициентов:
|
|
|
|
|
|
Анализ корней показывает, что система устойчива, поскольку все корни расположены в левой полуплоскости.
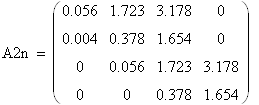
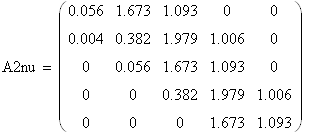
7.5.2 Замкнутая система с И – регулятором по возмущениюСоставим вектор коэффициентов:
|
|
|
|
|
|
Анализ корней показывает, что система устойчива, поскольку все корни расположены в левой полуплоскости.
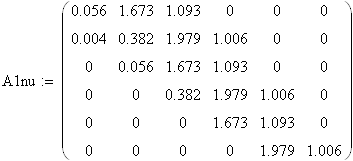
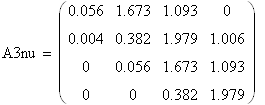
7.5.3 Замкнутая система с ПИ – регулятором по возмущению
Составим вектор коэффициентов:
|
|
|
|
|
|
Анализ корней показывает, что система устойчива, поскольку все корни расположены в левой полуплоскости.
7.6 Проверка устойчивости САУ по критерию устойчивости ГурвицаСистема, описываемая передаточной функцией:
![]() ,
,
или линейным дифференциальным уравнением:
![]() ,
,
будет устойчивой, если все корни ее характеристического уравнения имеют отрицательные действительные части. А для этого необходимо и достаточно, чтобы определитель А. Гурвица (1895 г.), составленный в следующем виде:
 ,
,
и все его диагональные миноры:
![]() ;
; 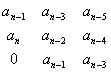 ,
,
и.т.д. были одного знака с ![]() . При выборе знака
. При выборе знака ![]() определитель Гурвица и все его диагональные миноры должны бать положительны.
определитель Гурвица и все его диагональные миноры должны бать положительны.
Как следствие этого, необходимое условие устойчивости будет следующие, что все коэффициенты характеристического уравнения должны быть положительны.
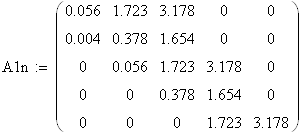
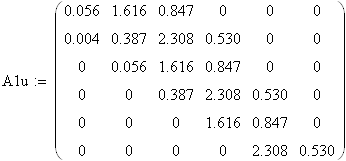
7.6.1 Замкнутая система с П – регулятором по управлениюОбщий вид передаточной функции замкнутой системы с П – регулятором по управлению:
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По результатам расчёта все миноры определителя Гурвица ![]() ,
, ![]() ,
, ![]() и
и ![]() вместе с коэффициентом
вместе с коэффициентом ![]() положительны, значит замкнутая система, описываемая этой передаточной функцией, устойчива.
положительны, значит замкнутая система, описываемая этой передаточной функцией, устойчива.
7.6.2 Замкнутая система с И – регулятором по управлению
Общий вид передаточной функции замкнутой системы с И – регулятором по управлению:
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По результатам расчёта все миноры определителя Гурвица ![]() ,
, ![]() ,
, ![]() и
и ![]() вместе с коэффициентом
вместе с коэффициентом ![]() положительны, значит замкнутая система, описываемая этой передаточной функцией, устойчива.
положительны, значит замкнутая система, описываемая этой передаточной функцией, устойчива.
7.6.3 Замкнутая система с ПИ – регулятором по управлению
Общий вид передаточной функции замкнутой системы с ПИ – регулятором по управлению:
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По результатам расчёта все миноры определителя Гурвица ![]() ,
, ![]() ,
, ![]() и
и ![]() вместе с коэффициентом
вместе с коэффициентом ![]() положительны, значит замкнутая система, описываемая этой передаточной функцией, устойчива.
положительны, значит замкнутая система, описываемая этой передаточной функцией, устойчива.
Для исследования устойчивости замкнутой системы по критерию Михайлова строится годограф вектора характеристического уравнения знаменателя замкнутой системы при изменении частоты ![]() от
от ![]() до
до ![]() . Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от
. Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от ![]() до
до ![]() , начав свое движение с положительной действительной полуоси и вращаясь против часовой стрелки, последовательно проходил
, начав свое движение с положительной действительной полуоси и вращаясь против часовой стрелки, последовательно проходил ![]() квадрантов, нигде не обращаясь в нуль (где
квадрантов, нигде не обращаясь в нуль (где ![]() - порядок характеристического уравнения).
- порядок характеристического уравнения).
Таким образом, для исследования системы на устойчивость по критерию Михайлова необходимо построить годограф знаменателя передаточной функции замкнутой системы и по его виду оценить ее устойчивость.
Необходимо заметить, что для адекватного отображения годографа в области малых и больших частот часто приходиться строить несколько вариантов этого годографа в различных диапазонах частот, чтобы просмотреть его поведение во всем диапазоне.
7.7.1 Замкнутая система с П – регулятором по возмущению![]()
Общий вид передаточной функции замкнутой системы с П – регулятором по возмущению:
|
|
| - диапазон изменения чатоты; |
|
|
| - замена p на комплексную величину i; |
|
|
| - знаменатель передаточной функции; |
|
|
| - действительная составляющая; |
|
|
| - мнимая составляющая; |
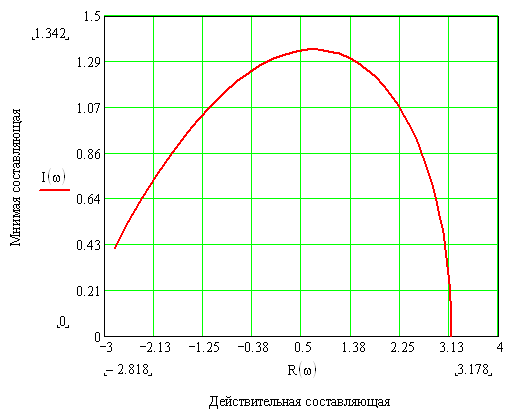
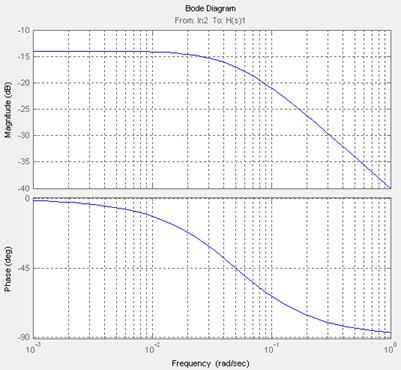
Рисунок 18 – Годограф Михайлова разомкнутой системы с П – регулятором в интервале частот [0;2]
Изменим диапазон частоты:![]() и покажем, что годограф разомкнутой системы с П – регулятором проходит все 5 квадрантов.
и покажем, что годограф разомкнутой системы с П – регулятором проходит все 5 квадрантов.
|
|
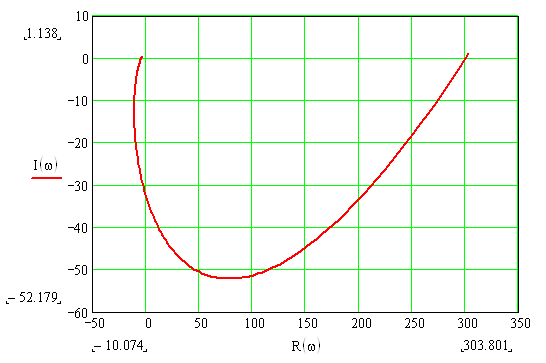
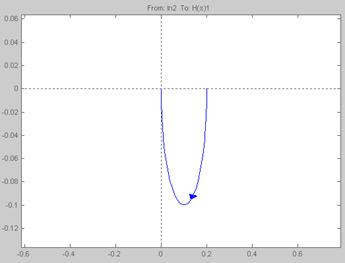
Рисунок 19 – Годограф Михайлова разомкнутой системы с П – регулятором в интервале частот [2;9,5]
Из рисунков 18 и 19 видно, годограф проходит 5 квадрантов, начав свое движение с положительной действительной полуоси, вращаясь последовательно против часовой стрелки нигде не обращаясь в нуль. Таким образом, замкнутая система с П – регулятором является устойчивой, так как выполняется необходимое и достаточное условие устойчивости по критерию Михайлова.
7.7.2 Замкнутая система с И – регулятором по возмущению
Общий вид передаточной функции замкнутой системы с ПИ – регулятором по возмущению:
|
|
| - диапазон изменения чатоты; |
|
|
| - замена p на комплексную величину i; |
|
|
| - знаменатель передаточной функции; |
|
|
| - действительная составляющая; |
|
|
| - мнимая составляющая; |
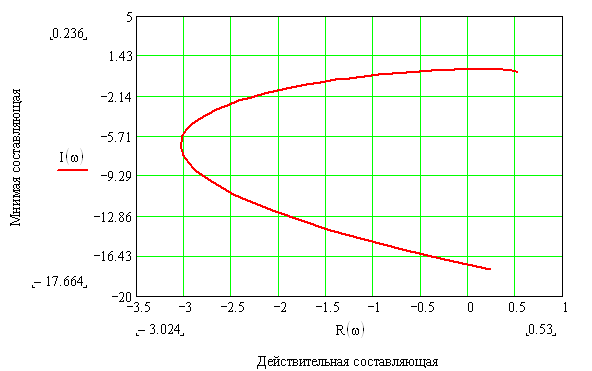
Рисунок 20 – Годограф Михайлова разомкнутой системы с И – регулятором в интервале частот [0;2,5]
Изменим диапазон частоты:![]() и покажем, что годограф разомкнутой системы с И – регулятором проходит все 6 квадрантов.
и покажем, что годограф разомкнутой системы с И – регулятором проходит все 6 квадрантов.
![]()
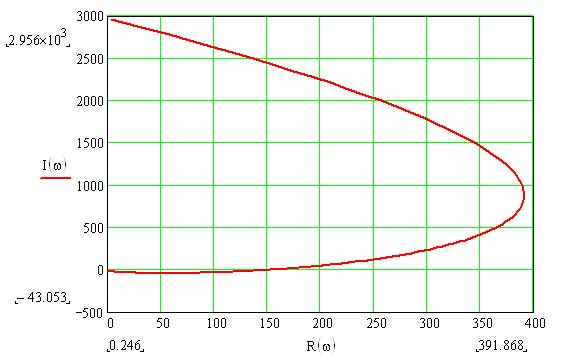
Рисунок 21 – Годограф Михайлова разомкнутой системы с И – регулятором в интервале частот [2,5; 9,5]
Из рисунков 20 и 21 видно, годограф проходит 6 квадрантов, начав свое движение с положительной действительной полуоси, вращаясь последовательно против часовой стрелки нигде не обращаясь в нуль. Таким образом, замкнутая система с И – регулятором является устойчивой, так как выполняется необходимое и достаточное условие устойчивости по критерию Михайлова.
7.7.3 Замкнутая система с ПИ – регулятором по возмущению
Общий вид передаточной функции замкнутой системы с ПИ – регулятором по возмущению:
![]()
|
|
| - диапазон изменения чатоты; |
|
|
| - замена p на комплексную величину i; |
| - знаменатель передаточной функции; |
|
|
| - действительная составляющая; |
|
|
| - мнимая составляющая; |
|
|
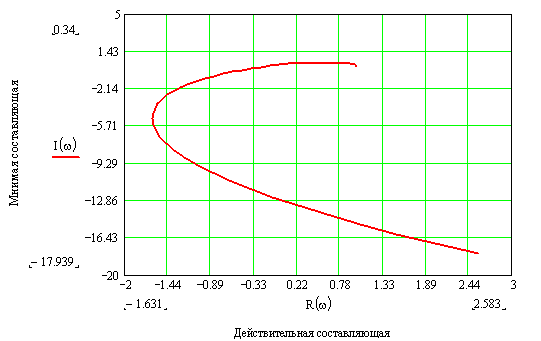
Рисунок 22 – Годограф Михайлова разомкнутой системы с ПИ – регулятором в интервале частот [0;2,5]
Изменим диапазон частоты:![]() и покажем, что годограф разомкнутой системы с ПИ – регулятором проходит все 6 квадрантов.
и покажем, что годограф разомкнутой системы с ПИ – регулятором проходит все 6 квадрантов.
![]()
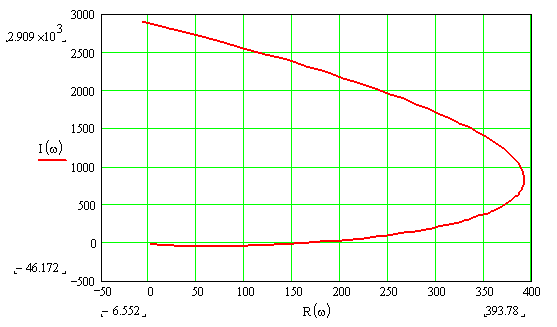
Рисунок 23 – Годограф Михайлова разомкнутой системы с ПИ – регулятором в интервале частот [2,5; 9,5]
Из рисунков 22 и 23 видно, годограф проходит 6 квадрантов, начав свое движение с положительной действительной полуоси, вращаясь последовательно против часовой стрелки нигде не обращаясь в нуль. Таким образом, замкнутая система с ПИ – регулятором является устойчивой, так как выполняется необходимое и достаточное условие устойчивости по критерию Михайлова.
8 ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ 8.1 Постановка задачи. Методы решения
Чтобы окончательно убедиться в пригодности САУ нужно исследовать результаты их переходных процессов. Поэтому на завершающей стадии проектирования САУ всегда стремятся тем или иным способом получить оценки динамических характеристик системы и сравнить их с заданными.
Переходные процессы рассчитывают для замкнутых САУ по возмущающему и управляющему воздействиям. Если переходные процессы рассчитываются для замкнутых САУ по возмущению, то регулятор должен в течение переходного процесса скомпенсировать это возмущение, а объект – вернуться в исходное состояние, в котором он был до приложения возмущения. Если же переходные процессы рассчитываются для замкнутых САУ по управлению, то регулятор должен отработать управляющее воздействие и регулируемая величина на выходе объекта должна принять заданное значение.
Для построения переходных процессов, используя при этом любые методы (аналитические, численные), необходимо иметь математическую модель замкнутой системы в форме передаточной функции или дифференциального уравнения (ДУ).
Если передаточная функция замкнутой системы приведена к ДУ с произвольной правой частью, то аналитическое решение ищется в следующей последовательности:
– находятся корни характеристического уравнения;
– строится частное решение с неопределенными коэффициентами;
– полученное частное решение подставляется в исходное уравнение;
– после приравнивания коэффициентов при одинаковых степенях ![]() находятся все неопределенные коэффициенты;
находятся все неопределенные коэффициенты;
– записывается искомое частное решение.
Это решение и будет являться зависимостью выходной координаты системы от времени.
При использовании численных методов для построения переходных процессов необходимо:
– передаточную функцию замкнутой системы преобразовать в ДУ;
– ДУ ![]() порядка привести к нормальной системе, состоящей из
порядка привести к нормальной системе, состоящей из ![]() ДУ первого порядка;
ДУ первого порядка;
– задать уравнение для возмущающего воздействия;
– выбрать один из численных методов для решения полученной системы;
– составить программу на ЭВМ для решения полученной системы ДУ и построения переходных процессов.
Для решения поставленной задачи используются следующие методы:
1) Метод Эйлера;
Интегрирование ДУ этим методом аналогично вычислению определенного интеграла по методу левых прямоугольников:
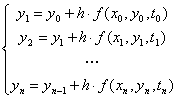 .
.
2) Модифицированный метод Эйлера
Аналогично методу средних прямоугольников:
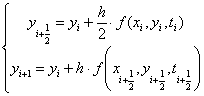 .
.
Недостатком данного метода являются двойные затраты на решение.
3) Усовершенствованный метод Эйлера-Коши
Аналогично методу трапеций:
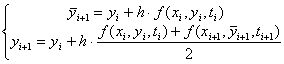 .
.
4) Метод Эйлера – Коши с итерациями
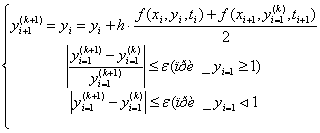
В данном методе приближенное решение используется для уточнения этого же решения (подстановка в правую часть), эта итерация продолжается до обеспечения требуемой точности; если точность не достигается за заданное количество итераций, то либо нужно изменить дополнительное число итераций, либо уменьшить требуемую точность;
5) Методы с автоматическим выбором величины шага (адаптивные)
Во всех численных методах точность зависит от величины шага, в то же время искомое решение изменяется с разной скоростью внутри интервала. Для численных методов необходимо выбрать разный шаг на разных участках изменения функции, чтобы обеспечить на них одинаковую точность. В этих методах решение на каждом шаге находится дважды: с исходным шагом и с шагом, в два раза меньшим. Эти два решения сравниваются, и если точность не достигнута, то исходный шаг уменьшается вдвое и процедура повторяется; таким образом, каким бы ни был исходный шаг, машиной выберется шаг в соответствии с заданной точностью. В такой процедуре шаг может быть выбран исключительно малым и прохождение всего интервала с таким шагом может оказаться неэффективным, поэтому на следующем шаге выполняется обратная процедура. Решение находится с этим же шагом и с шагом в два раза большим; если точность достаточна, то шаг увеличивается еще вдвое. Таким образом, величина шага однозначно определяется величиной дополнительной погрешности получения решения;
6) Метод Рунге – Кутта:
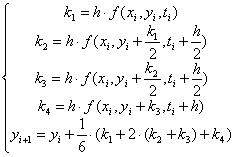 .
.
7) Экстраполяционные методы
В основе этих методов лежит получение решения в последующей точке через найденные решения в предыдущих точках;
8) Методы решения для жестких систем (метод Гира, метод Штера, метод Булирша)
Для этого вычисляется матрица Якоби:
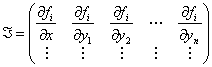 .
.
Запишем передаточную функцию данной системы:
![]() .
.
По аналогии с п.5 преобразуем полученную передаточную функцию в ДУ пятого порядка и приведем его к нормальной системе. После этого зададим нормальную систему в виде вектора.
Запишем нормальную систему и решим её:
|
|
|
|
|
|
|
|
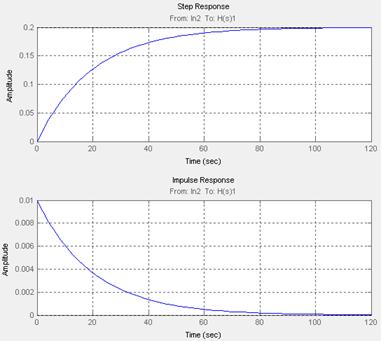
Полученные результаты отобразим на рисунке 24.
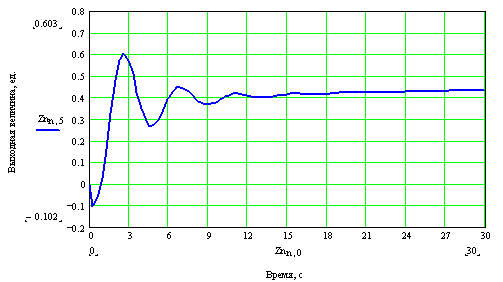
Рисунок 24 – График переходного процесса в замкнутой системе с П – регулятором по возмущению
8.2.2 Система с И – регулятором
Запишем передаточную функцию данной системы:
![]() .
.
По аналогии с п.5 преобразуем полученную передаточную функцию в ДУ шестого порядка и приведем его к нормальной системе. После этого зададим нормальную систему в виде вектора.
Запишем нормальную систему и решим её:
|
|
|
|
|
|
|
|
Полученные результаты отобразим на рисунке 25.
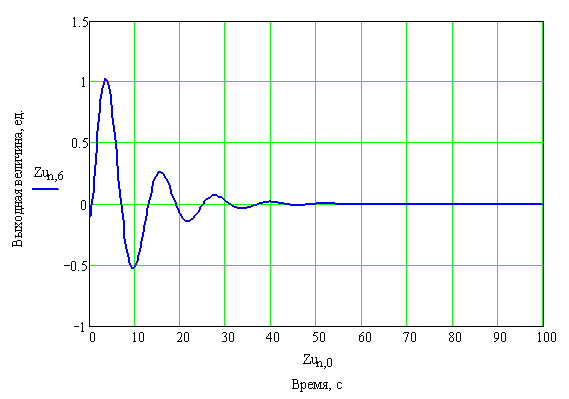
Рисунок 25 – График переходного процесса в замкнутой системе с И – регулятором по возмущению
8.2.3 Система с ПИ – регуляторомЗапишем передаточную функцию данной системы:
![]() .
.
По аналогии с п.5 преобразуем полученную передаточную функцию в ДУ шестого порядка и приведем его к нормальной системе. После этого зададим нормальную систему в виде вектора.
Запишем нормальную систему и решим её:
|
|
|
|
|
|
![]()
Полученные результаты отобразим на рисунке 26.
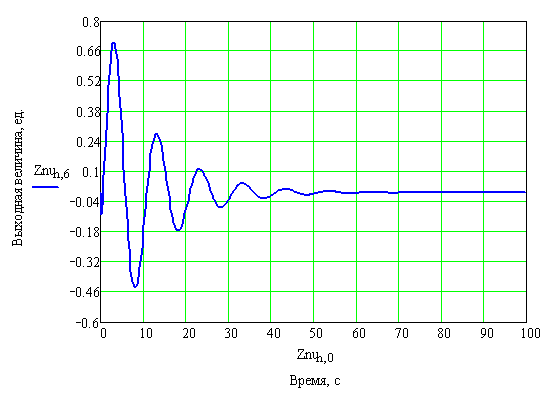
Рисунок 26 – График переходного процесса в замкнутой системе с ПИ – регулятором по возмущению
8.3 Построение переходных процессов в замкнутых системах по управлению 8.3.1 Система с П – регулятором
Запишем передаточную функцию данной системы:
![]()
По аналогии с п.5 преобразуем полученную передаточную функцию в ДУ пятого порядка и приведем его к нормальной системе. После этого зададим нормальную систему в виде вектора.
Запишем нормальную систему и решим её:
|
|
|
|
|
|
|
|
Полученные результаты отобразим на рисунке 27.
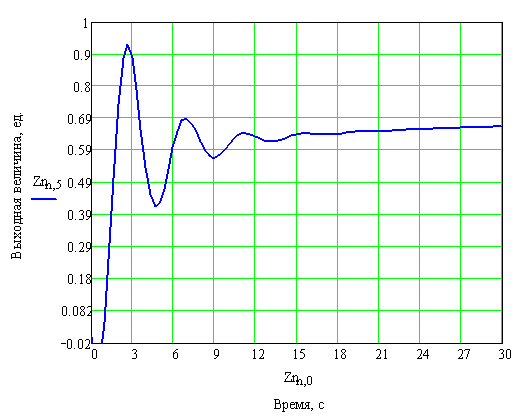
Рисунок 27 – График переходного процесса в замкнутой системе с П – регулятором по управлению
8.3.2 Система с И – регуляторомЗапишем передаточную функцию данной системы:
![]()
По аналогии с п.5 преобразуем полученную передаточную функцию в ДУ шестого порядка и приведем его к нормальной системе. После этого зададим нормальную систему в виде вектора.
Запишем нормальную систему и решим её:
|
|
|
|
|
|
|
|
Полученные результаты отобразим на рисунке 28.
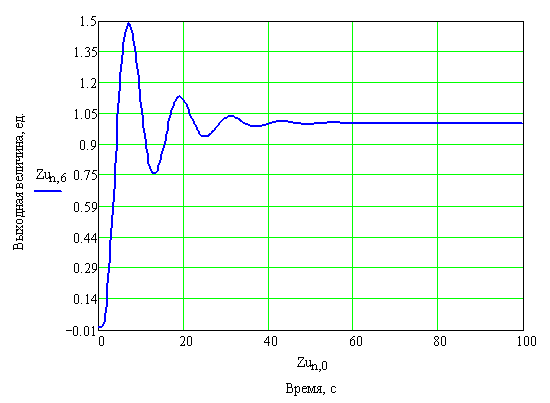
Рисунок 28 – График переходного процесса в замкнутой системе с И – регулятором по управлению
8.3.3 Система с ПИ – регуляторомЗапишем передаточную функцию данной системы:
![]()
По аналогии с п.5 преобразуем полученную передаточную функцию в ДУ шестого порядка и приведем его к нормальной системе. После этого зададим нормальную систему в виде вектора.
Запишем нормальную систему и решим её:
|
|
|
|
|
|
|
|
Полученные результаты отобразим на рисунке 29.
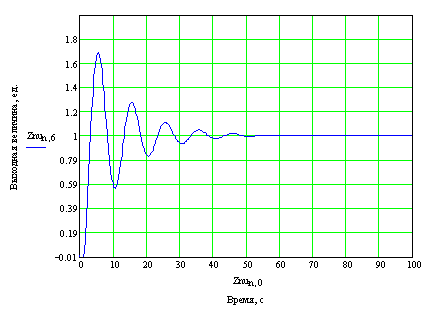
Рисунок 29 – График переходного процесса в замкнутой системе с ПИ – регулятором по управлению
Похожие работы
... , является то, что в замкнутой системе все физические величины, представляющие воздействие одного звена на другое, связаны в единую замкнутую цепь. Автоматические системы регулирования должны обеспечивать: - устойчивость системы при любых режимных ситуациях объекта; - минимальное время регулирования; - минимальные динамические и статические отклонения регулируемой величины, не выходящие ...
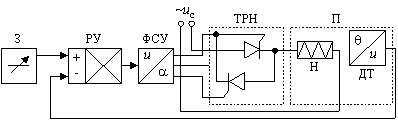
... , поддерживало температуру на нужном уровне. Установка требуемой температуры осуществляется с помощью задатчика (З). 1.2 Описание структурной схемы Рис. 2. Структурная схема автоматической системы регулирования температуры Входным сигналом системы является напряжение Uз, оно сравнивается с напряжением Uд ≈ Θ, которое действует на выходе датчика. Если Uз ≠ Uд, то ...
... на основе правил Госгортехнадзора с учетом местных условий и особенностей оборудования. Котел должен быть оборудован необходимым количеством контрольно-измерительных приборов, автоматической системой регулирования важнейших параметров котла, защитными устройствами, блокировкой и сигнализацией. Режимы работы котла должны соответствовать режимной карте, в которой указываются рекомендуемые ...
... системой: время наработки на отказ системы увеличилось на 2,73%. Вывод В ходе курсовой работы было произведено техническое обеспечение автоматической системы регулирования качества стабильного гидрогенизата. Были выбраны средства контроля и регулирования и обоснован их выбор. Был произведен расчет надежности контура регулирования, и предложена схема для резервирования самого ненадежного ...
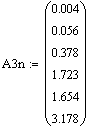
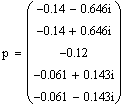
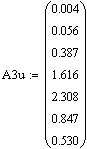

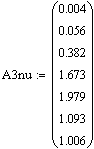











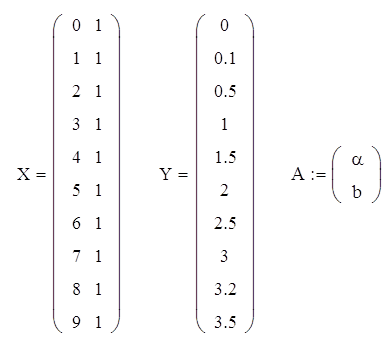
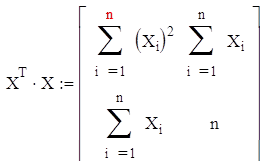
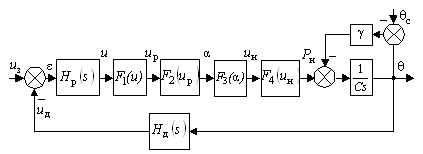
0 комментариев