Навигация
Проверка гипотез о статистической значимости оценок параметров модели на основе F- и t-критериев
5. Проверка гипотез о статистической значимости оценок параметров модели на основе F- и t-критериев
5.1 Проверка адекватности модели по критерию Фишера
Проверку адекватности модели по критерию Фишера проведем по представленному алгоритму.
Шаг 1. Формулирование нулевой и альтернативной гипотез.
![]() , т.е. не один фактор модели не влияет на показатель.
, т.е. не один фактор модели не влияет на показатель.
![]() Хотя бы одно значение
Хотя бы одно значение ![]() отменно от нуля, т.е.
отменно от нуля, т.е. ![]()
Шаг 2. Выбор соответствующего уровня значимости.
Уровнем значимости ![]() называется вероятность сделать ошибку 1-го рода, т.е. отвергнуть правильную гипотезу. Величина
называется вероятность сделать ошибку 1-го рода, т.е. отвергнуть правильную гипотезу. Величина ![]() называется уровнем доверия или доверительной вероятностью.
называется уровнем доверия или доверительной вероятностью.
Выбираем уровень значимости ![]() , т.е. доверительная вероятность – Р=0,95
, т.е. доверительная вероятность – Р=0,95
Шаг 3. Вычисление расчетного значения F-критерия.
Расчетное значение F-критерия определяется по формуле:

Для проверки полученного значения скопируем с итогового листа Регрессия расчетное значение F-критерия. Значения совпали ![]()
Шаг 4. Определение по статистическим таблицам F-распределения Фишера критического значения F-критерия.
Критическое значение F-критерия находим по статистическим таблицам F-распределения Фишера по соответствующим данным:
- доверительной вероятности Р=0,95 ;
- степеней свободы ![]()
Определяем табличное значение критерия ![]() =5,14
=5,14
Шаг 5. Сравнение рассчетного значения F-критерия с критическим и интерпритация результатов.
Вывод о принятии нулевой гипотезы, т.е. об адекватности модели делаем с помощью встроенной логической функции ЕСЛИ.
Поскольку ![]() ,то отвергаем нулевую гипотезу про незначимость факторов с риском ошибиться не больше чем на 5% случаев, т.е. с надежностью Р=0,95 можно считать, что принятая модель адекватна статистическим данным и на основе этой модели можно осуществлять экономический анализ и прогнозирование.
,то отвергаем нулевую гипотезу про незначимость факторов с риском ошибиться не больше чем на 5% случаев, т.е. с надежностью Р=0,95 можно считать, что принятая модель адекватна статистическим данным и на основе этой модели можно осуществлять экономический анализ и прогнозирование.
5.2 Проверка значимости оценок параметров модели по критерию Стьюдента
Проверку гипотезы о значении каждого параметра модели проведем в соответствии с представленным алгоритмом.
Шаг 1. Формулирование нулевой и альтернативной гипотез.
![]() - оценка j-го параметра является статистически незначимой, т.е. j-й фактор никак не влияет на показатель у;
- оценка j-го параметра является статистически незначимой, т.е. j-й фактор никак не влияет на показатель у;![]()
![]() - оценка j-го параметра является статистически значимой, т.е. j-й фактор влияет на показатель у.
- оценка j-го параметра является статистически значимой, т.е. j-й фактор влияет на показатель у.
Шаг 2. Выбор соответствующего уровня значимости.
Выбираем уровень значимости ![]() , т.е. доверительная вероятность – Р=0,95.
, т.е. доверительная вероятность – Р=0,95.
Шаг 3. Вычисление расчетного значения t-критерия.
Расчетное значение t-критерия определяется по формуле:
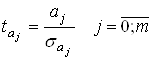
Во время анализа двухфакторной модели расчетные значения t-критерия определяются по формулам:
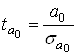 =-3,2333
=-3,2333 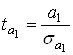 =3,4264
=3,4264 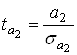 =4,9937
=4,9937
Для проверки полученного значения t-критерия скопируем с итогового листа Регрессия значения ячеек столбца t-статистика. Значения совпали.
Шаг 4. Определение по статистическим таблицам t-распределения Стьюдента критического значения t-критерия.
Критическое значение t-критерия находим по статистическим таблицам t-распределения Стьюдента по соответствующим данным:
- доверительной вероятности Р=0,95 ;
- степеней свободы ![]()
Определяем табличное значение критерия ![]() =2,45
=2,45
Шаг 5. Сравнение рассчетного значения t-критерия с критическим и интерпритация результатов.
Выводы о принятии нулевой гипотезы, т.е. о значимости оценок параметров ![]() ,
, ![]() и
и ![]() делаем с помощью встроенной логической функции ЕСЛИ. С надежностью Р=0,95 можно считать, что
делаем с помощью встроенной логической функции ЕСЛИ. С надежностью Р=0,95 можно считать, что
- оценки 1-го и 2-го параметров модели значимые, т.е. оба фактора существенно влияют на показатель;
- оценка 0-го параметра модели не является статистически значимой.
Таблица 9 – Проверка гипотез о статистической значимости оценок параметров модели на основе F- и t- критериев
| F-критерий Фишера | |||
| По формуле | Регресия | Р=0.95 | |
| F | 2,45 | ||
| 0,810187427 | 0,810187 | Модель не адекватна | |
| t-критерий Стьюдента | |||
| По формуле | Регресия | Р=0.95 | |
| t-статистика | 5,14 | ||
| 2,278334309 | 2,278334 | а0 | Параметр не значимый |
| -1,00461334 | -1,00461 | а1 | Параметр не значимый |
| -0,02017108 | -0,02017 | а2 | Параметр не значимый |
Похожие работы
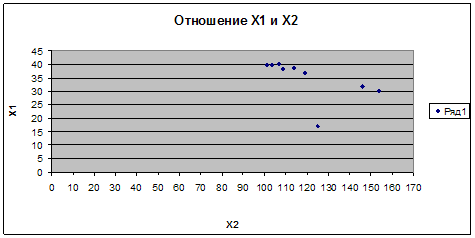
... 1 2,32 38,8 114 2 2,19 39,9 101,1 3 2,83 30,1 153,8 4 2,75 31,7 146 5 2,59 17,2 124,8 6 2,27 39,7 103,6 7 2,05 36,9 119 8 1,95 38,2 108,7 9 2,08 40,1 106,5 Построение и анализ классической многофакторной линейной эконометрической модели 1. Спецификация модели 1.1 Идентификация переменных Многофакторная линейная эконометрическая модель устанавливает линейную ...
... , о величине, характере и причинах отклонений в деятельности изучаемых объектов, а также об имеющихся резервах производства. Таким образом, основная задача экономического анализа подразделяется на следующие, более локальные задачи: · оценка работы предприятия и его подразделений за определенные промежутки времени; · выявление положительных и отрицательных факторов, влияющих на работу ...
... объектов; б) наличие данных за предыдущий период; в) наличие базисных данных; г) сопоставимость данных. 26. По характеру принимаемых решений экономический анализ подразделяется: а) предварительный, текущий и заключительный б) оперативный, ретроспективный и перспективный в) предварительный, последующий и итоговый 27. Информация, ...
... (соединение отдельных элементов в общий показатель). Таким образом, финансовый анализ играет огромную роль в аудиторской деятельности, способен оказать существенное влияние на дальнейшее развитие экономического субъекта его место в рыночной экономике. Качественный финансовый анализ - основа всего процесса аудиторской проверки, поэтому ему уделяется самое пристальное внимание как аудиторской ...

0 комментариев