Навигация
Особливості полів допуску підшипників кочення
9.3 Особливості полів допуску підшипників кочення
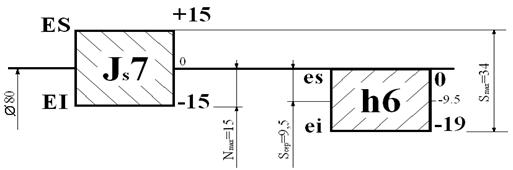
Поля допусків D і d підшипника кочення розташовані нижче нульової лінії. Таким чином, поле допуску D займає таке ж положення, як поле допуску основного вала, а поле допуску d в порівнянні з полем допуску основного отвору перевернено щодо нульової лінії.
Поля допусків, по яких обробляють посадкові поверхні валів і отворів у корпусах у з’єднанні з полями допусків, установленими на D і d підшипників, утворять спеціальні посадки.
Система допусків і посадок підшипників кочення заснована на системі допусків і посадок гладких циліндричних поверхонь з деякими особливостями:
а) значення граничних відхилень на D і d залежать тільки від класу точності підшипників і не залежить від характеру з’єднання підшипника з корпусами і валами (таблиця 1).
Таблиця 1
| Клас точності | Поля допусків валів | Поле допусків отворів |
| 5 і 4 | n5 m5 k5 js5 h5 g5 Г1 Т1 Н1 П1 С1 Д1 | N6 M6 K6 Js6 H6 Г1 Т1 Н1 П1 С1 |
| 0 і 6 | n6 m6 k6 js6 h6 g6 f6 I Т Н П С Д X | P7 N7 M7 K7 Js7 H7 G7 H8 H9 Р Г Т Н Р С Д С3 |
Оптимальними полями допусків розмірів деталей, що з’єднуються з підшипниками кочення, вважаються ті, котрі забезпечують найменші натяги і зазори.
Рекомендується: Вибираючи поле допусків для розмірів, рекомендують кільцю, що обертається разом з деталлю (валом, корпусом), за допомогою посадки забезпечувати нерухомість з'єднання, а кільцю, що не обертається – рухливість з'єднання. Це забезпечує рівномірність зносу направляючих доріжок унаслідок часткового провертання нерухомого кільця в напрямку руху його рухливого кільця і тіл кочення (кульок, роликів) (таблиця 2, 3, 4, 5). Наприклад:
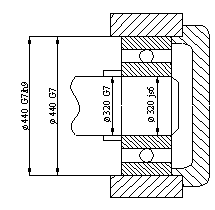
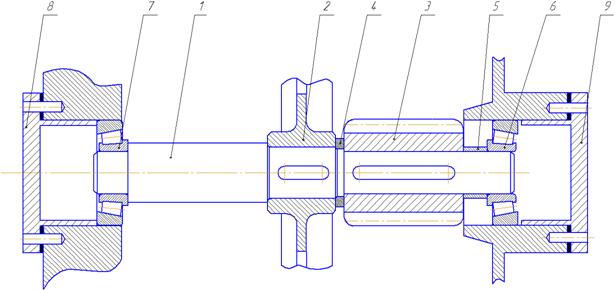
Рис. 1 Підшипниковий вузол
9.4 Типи навантаження підшипників кочення
При виборі посадок по приєднувальних поверхнях підшипників ураховують величину й напрямок діючих на підшипник навантажень, частоту обертання, тип підшипника, його температуру, умови монтажу і вид навантаження, що залежить від того, обертається чи ні кільце щодо радіального навантаження. Навантаження може бути місцевим, циркуляційним і коливальним. Кільце випробовує місцеве навантаження, якщо воно щодо радіального навантаження не обертається, а навантаження сприймає лише певна ділянка доріжки кочення цього кільця - у цьому випадку посадка призначається із зазором.
При циркуляційному навантаженні кільця радіальне навантаження щодо кільця (або кільце щодо навантаження) обертається. Тіла кочення в процесі обертання передають сприйману ними радіальне навантаження доріжці кочення послідовно по всій окружності. Посадка призначається послідовно. При коливальному навантаженні на кільце одночасно діють постійна по напрямку сила і обертова сила. Характер навантаження, прикладеної до кільця, у кожен момент часу визначається рівнодіючої цих сил, а посадка вибирається із числа щільно рухливих. При обертовому валу з'єднання внутрішнього кільця підшипника повинне бути нерухомим, а по зовнішньому діаметрі підшипника можливий невеликий зазор.
Якщо вал нерухомий, а обертається корпус із зовнішнім кільцем підшипника, то нерухома посадка повинна бути за зовнішнім діаметром підшипника, а за внутрішнім діаметром підшипника може бути і невеликий зазор із валом.
Таблиця 2
Рекомендовані поля допусків валів та отворів корпусів для підшипників кочення з циркуляційно-навантаженим кільцем
| Діаметр, мм | P2 кн/м | |||
| Поля допусків валів для внутрішнього кільця підшипника | js5; js6 | k5; k6 | m5; m6 | n5; n6 |
| Понад 18 до 80 | до 300 | 300 – 1400 | 1400 – 1600 | 1600 – 3000 |
| Понад 80 до 180 | до 600 | 600 – 2000 | 2000 – 2500 | 2500 – 4000 |
| Понад 180 до 360 | до 700 | 700 – 3000 | 3000 – 3500 | 3500 – 6000 |
| Понад 360 до 630 | до 900 | 900 – 3500 | 3500 – 4500 | 4500 – 8000 |
| Поля допусків отворів для зовнішнього кільця підшипника | K6; K7 | M6; M7 | №6; №7 | P7 |
| Понад 50 до 180 | до 800 | 800 – 1000 | 1000 – 1300 | 1300 – 2500 |
| Понад 180 до 360 | до 1000 | 1000 – 1500 | 1500 – 2000 | 2000 – 3300 |
| Понад 360 до 630 | до 1200 | 1200 – 2000 | 2000 – 2600 | 2600 – 4000 |
| Понад 630 до 1600 | до 1600 | 1600 – 2500 | 2500 – 3500 | 3500 - 5500 |
Таблиця 3
Рекомендовані поля допусків валів та отворів корпусів підшипників кочення з місцево-навантаженими кільцями
| Характер навантаження | Тип підшипника | Номінальний діаметр d або D, мм | Рекомендовані поля допусків | |
| валів | отворів у нероз’ємному корпусі | |||
| Навантаження спокійне або зі зваженими точками та вібрацією, пере навантаження до 150%, при КП = 1.0 | Усі типи, крім штампованих голчатих | До 80 | h6; h5 | H7; H6 |
| Св. 80 до 260 | q6; q5 | G7; G6 | ||
| Св. 260 до 500 | js6; js5 | |||
| Навантаження з ударами та вібрацією, пере навантаження до 300% при КП = 1.8 | Усі типи, крім штампованих голчатих та роликових конічних дворядних | До 80 | h6; h5 | JS7; JS6 |
| Св. 80 до 260 | H7; H6 | |||
| Св. 260 | q6; q5 | |||
Таблиця 4
Точність розмірів внутрішніх кілець підшипників радіальних шарикових та роликових (по СТ СЄВ 774-77)
| Номінальний діаметр отвору, d, мм | Середній діаметр отвору внутрішнього кільця, dm | Ширина кільця, В | |||||
| Класи точності підшипників | |||||||
| 0,6,5,4 | 0 | 6 | 5 | 4 | 0,6,5,4 | ||
| Допустимі відхилення, мкм | |||||||
| верхнє | нижнє | нижнє | нижнє | нижнє | верхнє | нижнє | |
| Понад 18 до 30 | 0 | -10 | -8 | -6 | -6 | 0 | -120 |
| Понад 30 до 50 | 0 | -12 | -10 | -8 | -6 | 0 | -120 |
| Понад 50 до 80 | 0 | -15 | -12 | -9 | -7 | 0 | -150 |
| Понад 80 до 120 | 0 | -20 | -15 | -10 | -8 | 0 | -200 |
| Понад 120до180 | 0 | -25 | -18 | -13 | -10 | 0 | -250 |
Таблиця 5
Точність розмірів внутрішніх кілець підшипників радіальних шарикових та роликових (по СТ СЄВ 774-77)
| Номінальний зовнішній діаметр, Д, мм | Середній діаметр отвору зовнішнього кільця, Дm | Радіальне биття доріжки кочення, мкм | |||||||
| Класи точності підшипників | |||||||||
| 0,6,5,4 | 0 | 6 | 5 | 4 | 0 | 6 | 5 | 4 | |
| Допустимі відхилення, мкм | |||||||||
| верхнє | нижнє | нижнє | нижнє | нижнє | не більше | ||||
| Понад 50 до 80 | 0 | -13 | -11 | -9 | -7 | 25 | 13 | 8 | 5 |
| Понад 80 до 120 | 0 | -15 | -13 | -10 | -8 | 35 | 18 | 10 | 6 |
| Понад 120 до 150 | 0 | -18 | -15 | -11 | -8 | 40 | 20 | 11 | 7 |
| Понад 150 до 180 | 0 | -25 | -18 | -13 | -10 | 45 | 23 | 13 | 8 |
| Понад 180 до 250 | 0 | -30 | -20 | -15 | -11 | 50 | 25 | 15 | 10 |
| Понад 250 до 315 | 0 | -35 | -25 | -18 | -13 | 60 | 30 | 18 | 11 |
Питання для самоперевірки:
1. Чим відрізняються підшипники кочення від підшипників ковзання?
2. Які тіла кочення Ви знаєте?
3. Перелічить серії підшипників кочення.
4. Як добирають поля допусків поверхонь, що контактують з підшипниками кочення?
5. Які є способи навантаження кілець підшипників кочення?
6. Які Ви знаєте способи добирання полів допусків розмірів поверхонь для з’єднань з підшипниками кочення?
7. Скільки посадочних місць Ви розраховуєте у підшипниковому вузлі?
8. Як добирають поля допусків поверхонь, що контактують з підшипниками кочення?
9. Які Ви знаєте способи добирання полів допусків розмірів поверхонь для з’єднань з підшипниками кочення?
Лекція №10
Тема: Відхилення та допуски форми поверхонь виробів та їх взаємного розміщення
10.1 Основні положення
При аналізі точності геометричних параметрів деталей розрізняють такі поверхні:
1. Номінальні (ідеальні);
2. Реальні (дійсні).
Аналогічно варто розрізняти номінальний і реальний профіль, номінальне і реальне розташування поверхні (профілю). Номінальне визначається номінальними лінійними і умовними розмірами, а реальне – дійсними.
Внаслідок відхилень дійсної форми від номінальної один розмір у різних перетинах деталі може бути різним.
Розміри в поперечному перерізі можна визначити змінним радіусом R, відлічуваним від геометричного центра номінального перетину. Цей радіус називають поточним розміром, тобто розміром, що залежить від положення осьової координати X (Б-Б) і кутової координати φ точки, що лежить на вимірюваній поверхні (φ - кутова координата радіуса R1).
φ - полярний кут. Контур поперечного перерізу задовольняє умові замкнутості, тобто f (φ) = f (φ+ 2π) (виходить, функція має період 2Т).
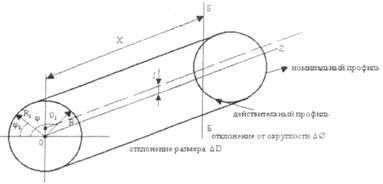
Для аналізу відхилень профілю контур перетину дійсної поверхні можна характеризувати сукупністю гармонійних складових із різними частотами.
Для аналітичного зображення дійсного профілю (контуру перетину) поверхні використають розкладання функції погрішностей f(φ) у ряд Фур'є.
Відхилення ΔR січного розміру R (при обраному значенні Х) від номінального (постійного) розміру R0, можна виразити залежністю:
ΔR=R-R0=f(φ)
Розглядаючи відхилення ΔR радіуса-вектора в полярній системі координат як функцію полярного кута φ, можна представити відхилення контуру поперечного переріза деталі у вигляді ряду Фур'є:
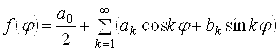 ,
,
де![]() - нульовий член розкладання
- нульовий член розкладання
ак, bк - коефіцієнти ряду Фур'є коливань гармоніки.
К - порядковий номер. Ряд Фур'є можна представити також у вигляді:
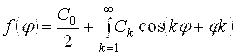 ,
,
де Ск - амплітуда коливань гармоніки.
φk - початкова фаза.
Функція f(φ) визначається сукупністю величин Ск, (спектра амплітуд) і φk (спектра фаз).
Далі використаємо ряд з обмеженим числом членів, тобто тригонометричний поліном:
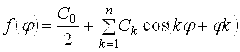
Відповідно до теорії Фур'є, нульовий член розкладання в загальному випадку є середнім значенням f(φ) за період 2π :
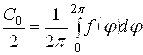 , тобто
, тобто ![]() -є постійна, складова відхилення поточного розміру.
-є постійна, складова відхилення поточного розміру.
1-й член розкладання С1cos(φ + φ1), виражає розбіжність центра обертання О с геометричним центром перетину О (ексцентриситет), тобто відхилення розташування поверхні. Тут С1, φ1 - амплітуда й фаза. Члени ряду, починаючи із 2-го і до К = р утворять спектр відхилень форми деталі в поперечному перерізі.

При цьому 2-й член ряду ![]() - виражає овальність, 3-й
- виражає овальність, 3-й ![]() - огранювання із 3-х верховим профілем. Наступні члени ряду, що мають номер К > р, виражають хвилястість, при досить великій кількості членів ряду одержуємо високочастотні складові, що виражають шорсткість поверхні.
- огранювання із 3-х верховим профілем. Наступні члени ряду, що мають номер К > р, виражають хвилястість, при досить великій кількості членів ряду одержуємо високочастотні складові, що виражають шорсткість поверхні.
Аналогічно можна представити відхилення контуру циліндричної поверхні в поздовжньому перерізі, але умова замкнутості контуру в цьому випадку не виконується, де z- змінна, що відлічується уздовж осі циліндра.
Уявивши циліндричну систему координат R, φ , Z і умовно прийнявши, що період Т=2Т, представимо відхилення контуру в поздовжньому перерізі f(z) у вигляді тригонометричного полінома:
![]() ,
,
де 0≤z≤ℓ
при К= 1
![]() ;
;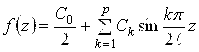 ,
,
де К- порядковий номер члена.

Перший член розкладання характеризує нахил утворюючого циліндра (конусоподібність).
Другий характеризує опуклість контуру в поздовжньому перерізі. Цей же 2-й - при наявності зсуву фази виражає сідлоподібність тощо.
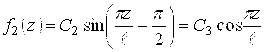
Похожие работы
... – 0,046 = 71,954 мм Визначимо граничні зазори: Smax = Dmax – dmin = 72,046 – 71,954 = 0,092 мм Smin = Dmin – dmax = 72,000 – 72,000 = 0,000 мм 3.4 Взаємозамінність нарізних сполучень Завдання: Для нарізного сполучення кришка складального креслення прийняти розміри нарізного сполучення й уточнити по стандарті. Призначити крок різьблення, середній діаметр і внутрішній діаметр різьблення. ...
... = = – 0,8 мм , тобто граничні відхилення складових ланок призначені правильно. 3.2 Розрахунок імовірнісним методом (пряма задача). Завдання 3.2. Для можливості порівняння з розрахунком за методом повної взаємозамінності розглянемо той же розмірний ланцюг (див. рис. 3.1). 1 - 3-й пункти аналогічні відповідним пунктам розв'язку методом повної взаємозамінності. 4. Приймаємо, що розсіювання ...
... і вал, надлишкова теплота буде видалятись примусовою прокачкою масла. 13. Визначаємо об’єм масла, що прокачується через підшипник: = 0,2 л/хв 2.2 Розрахунок допусків, посадок та параметрів посадок гладких циліндричних з’єднань Умова: Для трьох циліндричних з’єднань ( D1, D4, D5 ) підрахувати граничні розміри, допуски, величини найбільших, найменших і середніх зазорів (натягів), допуск ...
... напрессовываются подшипники поз.6 и 7. После этого вал устанавливается в редуктор с регулировкой осевой игры с помощью набора прокладок привертными крышками поз.8 и 9. Рисунок 1.- Сборочная единица (промежуточный вал редуктора) 2 ИСХОДНЫЕ ДАННЫЕ Тип производства – единичное. Передаваемый крутящий момент – 0,0722·103 Н*м. Частота вращения вала n =576 об/мин. Параметры шестерни: m n= ...
0 комментариев