Предположим, в какой-то стране производится два вида продукции: средства вооружения (ракеты) и продукты питания (масло) (табл.1.1)
Для каждого из семи вариантов производства указаны выпуски пяти продуктов и расходы трех ресурсов. Найти оптимальные по Парето варианты производства
Имеются следующие данные по экономике России (табл.2.1). Рассчитайте ВВП всеми возможными методами и статистическое расхождение в 20002002гг
На основе данных таблицы определите темпы прироста ВВП России в период 20002004гг., заполните пустые графы
Верно ли следующее утверждение: величины добавленной стоимости и стоимости конечной продукции равны между собой
Найти уровень безработицы, если уровень участия а%, взрослых 100 млн чел., работающих b млн. чел
За период октябрь ноябрь уровень инфляции составил а %, а в октябре – в %. Найти уровень инфляции в ноябре (с точностью до 0,1%)
Найти процентное изменение номинального ВВП за год, если годовой уровень инфляции равен а%, а падение реального ВВП равно b% (с точностью до 0,1%)
Дефлятор вырос с а до b при неизменном номинальном ВВП. Найти процентное изменение реального ВВП
Эффект процентной ставки заключается в следующем: при прочих равных условиях увеличение уровня цен:
Государство и внешний мир отсутствуют, тогда совокупные расходы (Е) состоят лишь из потребления и инвестиций (Е=C+I)
Внешний мир отсутствует, тогда доход состоит из потребления, инвестиций и государственных закупок: Y=C+I+G
В таблице заданы объемы потребления и налоговых поступлений при четырех различных значениях национального дохода (в млрд руб.)
Сравните структуру расходов бюджета в различных странах (табл. 6.2)[5]
Проанализируйте структуру доходов и расходов консолидированного бюджета по уровням бюджетной системы в 2005 году (табл. 6.3)[6]
Проанализируйте внутренние и внешние источники финансирования федерального бюджета в 2005 году (табл. 6.4)[7]
Чековые вклады банка равны 30 млн руб.; резервы – 10 млн руб., резервная норма – 25%. Найдите ссудный потенциал банка
Амортизация (износ капитала) составляет фиксированную долю (μ) капитала, она называется нормой амортизации: А = μK
Определите темпы экономического роста за год, если реальный ВВП в (t–1)-году составил 6000 млрд руб., а в t-году – 6400 млрд руб
Навигация
Внешний мир отсутствует, тогда доход состоит из потребления, инвестиций и государственных закупок: Y=C+I+G
Основы макроэкономики
230404
знака
170
таблиц
19
изображений
1. Внешний мир отсутствует, тогда доход состоит из потребления, инвестиций и государственных закупок: Y=C+I+G.
2. Инвестиции автономны, т.е. I =I0.
3. Потребление – линейная функция располагаемого дохода: С=С0+MPC*Yd.
Располагаемый доход (Yd) равен разности дохода и налоговых поступлений: Yd=Y–T.
4. Налоговые поступления (Т) есть линейная функция дохода, т.е. предельная налоговая ставка (t) постоянна: T=Т0+t*Y, где Т0 – автономные налоги (не зависящие от дохода).
Тогда
С=С0+MPC*Yd=С0+MPC*(Y–T)=С0+MPC*(Y–(Т0+t*Y))=
=С0+MPC*(Y– Т0 – – t*Y).
5. Государственные закупки автономны: G=G0.
Условие равновесия заключается в равенстве дохода и суммы потребления, инвестиций и государственных закупок:
Y=C+I+G=С0+MPC*(Y–Т0–t*Y)+I0+G0=С0+I0+G0+MPC*Y–MPC*Т0–MPC*t*Y = С0+ I0+ G0– MPC*Т0+ MPC*Y*(1–t)=А0+ MPC*Y*(1–t).
Т.е. Y= А0+ MPC*Y*(1–t) (1)
Решая уравнение (1) относительно дохода, получаем равновесный доход:
, (2)
где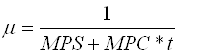 
– сложный мультипликатор, (3)
– автономные расходы. (4)
Прирост равновесного дохода превосходит вызвавший его прирост инвестиций (или государственных закупок, или того и другого вместе), причем отношение этих приростов равно сложному мультипликатору.
Сложный мультипликатор меньше простого, т.е. введение налогов ослабляет эффект мультипликации. Это отображается уменьшением угла наклона кривой совокупных расходов с увеличением налоговой ставки.
Мультипликатор сбалансированного бюджета равен отношению прироста дохода к вызвавшему его равному приросту государственных закупок и налоговых поступлений. Мультипликатор сбалансированного бюджета равен единице.
С изменением предельной налоговой ставки (t) изменяется равновесный доход и налоговые поступления. Кривая Лаффера изображает зависимость налоговых поступлений от предельной налоговой ставки. В целом кривая Лаффера напоминает параболу, однако она не симметрична (рис. 5.3).
Предельная налоговая ставка, обеспечивающая максимум налоговых поступлений (t*), обычно меньше 50%, причем с ростом MPS она увеличивается.
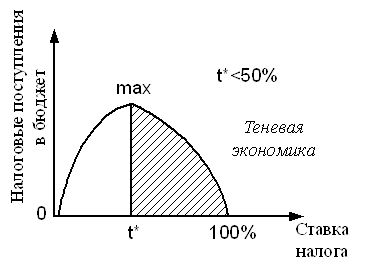
Рис. 5.3. Кривая Лаффера
В рамках кейнсианской модели с государством рассматривается модель кривой Лаффера, в которой предполагается, что налогом облагается превышение дохода над величиной автономных расходов, т.е. функция налоговых поступлений имеет вид: T=t*(Y-A0).
Тогда в условиях равновесия кривая Лаффера задается формулой:
T(t)=MPC*A0*(t-t2) / (MPS+MPC*t). (5)
При крайних значениях предельной налоговой ставки (t=0 и t=1) налоговые поступления равны нулю (T=0). Оптимальной называют предельную налоговую ставку (t*), при которой налоговые поступления максимальны (Tmax). Приравнивая производную от функции к нулю, получаем:
t*= MPS0,5 /(1+ MPS0,5). (6)
Налоговые поступления растут с увеличением предельной налоговой ставки, если она меньше оптимальной, и уменьшаются, если она больше оптимальной.
Пример 1. Предельная склонность к потреблению равна 0,8; предельная налоговая ставка равна 0,1. Найти изменение равновесного дохода при увеличении автономных инвестиций на 20 млрд. руб.
Решение:
Согласно формуле (3), сложный мультипликатор равен
m=1/(0,2+ 0,8*0,1) = 3,57.
Прирост равновесного дохода равен DY=m*DI
DY=3,57*20=71,4 (млрд руб.).
Пример 2. Автономные инвестиции, государственные закупки составляют в сумме 120. Потребление в системе без налогов равно C=40+0,8Y. Налоговые поступления равны Т=10+0,3Y. Найти равновесный доход и функцию потребления в системе с налогами.
Решение:
По формуле (4) автономные расходы равны
А0=120+40 0,8 * 10 = 152.
По формуле (3) сложный мультипликатор равен
m = 1/(0,2 + 0,8*0,3) = 2,3.
По формуле (2) равновесный доход равен Y = 2,3 * 152 = 349,6.
Для установления вида функции потребления в системе с налогами заменим в заданной функции потребления Y на (Y – Т). Получим, что потребление в системе с налогами задается формулой:
С= 40 + 0,8(Y– 10 – 0,3Y)= 32 +0,56Y.
Пример 3. Функция совокупных расходов Е = 72 + 0,64Y, предельная налоговая ставка t=20%. Найти изменение равновесного дохода при увеличении предельной налоговой ставки на пять пунктов.
Решение:
Из формулы (1) Y= А0+ MPC*Y*(1–t) следует, что МРС *0,8=0,64, отсюда МРС = 0,8.
Начальная величина сложного мультипликатора равна m0=1/(0,2+0,8*0,2) = =2,78.
Начальный равновесный доход равен Y0=72 * 2,78 = 200,2.
Конечная величина сложного мультипликатора равна
m1=1/(0,2 + 0,8 * 0,25) = 2,5.
Конечная величина равновесного дохода равна Y1= 72 * 2,5 = 180.
Таким образом, равновесный доход уменьшился на 20,2 в результате увеличения предельной налоговой ставки.
Пример 4. Автономные расходы равны А0=76, автономные налоги отсутствуют, предельная налоговая ставка t=10%, предельная склонность к потреблению MPC=0,9. Система находится в равновесии. Найти:
а) налоговые поступления;
б) располагаемый доход;
в) налоговые поступления после введения автономных налогов в объеме T0=12.
Решение:
Сложный мультипликатор равен m=1/ (0,1+0,9*0,1)=5,26.
Первоначальный равновесный доход равен Y0= 76*5,26=400.
Поскольку автономные налоги отсутствуют, налоговые поступления пропорциональны доходу: Т=0,1*400=40.
Располагаемый доход равен Yd=Y–T , т.е. Yd=400 – 40 =360.
Согласно формуле (4), введение автономных налогов T0=12 сократит автономные совокупные расходы на 0,9*12 =10,8 и их величина станет:
А1=76 – 10,8 = 65,2.
Новая величина равновесного дохода после введения автономных налогов: Y1=65,2 *5,26 =343.
Новая величина налоговых поступлений равна сумме автономных и неавтономных (зависящих от дохода) налогов: T1= 12+0,1*343=463.
Пример 5. МРС=0,75. Налоги выросли на 20 ден.ед. Государственные расходы увеличились также на 20 ден.ед. Рассчитать мультипликатор налогов. Найти изменение ВВП при одновременном росте налогов и совокупных расходов.
Решение:
Мультипликатор налогов равен mТ= -МРС/(1МРС).
mТ= -0,75/(10,75)=-3. При увеличении налогов совокупный спрос сократился на 60 ден.ед. (20*(-3)=-60).
Если госрасходы выросли на 20 ден.ед., то совокупный спрос вырос на 80 ден.ед:
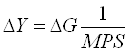=20*1/(10,75)=20*1/0,25=20*4=80 ден.ед.
Следовательно, при одновременном росте налогов и совокупных расходов на 20 ден.ед. ВВП вырастет на 20 ден.ед. (8060=20). Данный вывод подтверждает мультипликатор сбалансированного бюджета.
ЗАДАНИЯ
1. Автономные налоги увеличены на 50. Предельная склонность к потреблению MPC=0,8, предельная налоговая ставка t = 0,3. Найти изменение равновесного дохода.
2. При увеличении налоговой ставки с 30 до 40% налоговые поступления не изменились. Найти предельную склонность к потреблению.
3. Автономные расходы равны 14, предельная склонность к потреблению МРС = 0,9, предельная налоговая ставка t = 20%. Найти равновесный доход.
4. При увеличении предельной налоговой ставки с 50 до 60% равновесный доход уменьшился с 680 до 600. После этого установлена предельная налоговая ставка, равная t = 70%. Найти:
а) равновесный доход;
б) изменение равновесного дохода после увеличения автономных налогов на 76.
5. Потребление в системе без налогов равно C0 = 56 +0,9Y, а в системе с налогами равно C1 = 47+0,72Y. Автономное потребление составляет половину автономных расходов. Найти:
а) функцию налоговых поступлений;
б) налоговые поступления в условиях равновесия.
6. Автономное потребление, планируемые чистые инвестиции, государственные закупки и чистый экспорт составляют в сумме 6а+10b. Налоговые поступления равны T=а+b+0,5Y, предельная склонность к потреблению MPC=а/(а + b), автономное потребление C0 = а. Система находится в состоянии равновесия. Найти:
а) равновесный доход;
б) налоговые поступления;
в) располагаемый доход;
г) потребление.
7. Предельная склонность к потреблению равна MPC = 0,9, предельная налоговая ставка равна t = а/100. Найти:
а) прирост дохода, если государственные закупки увеличились на b;
б) прирост дохода, если автономные налоги увеличились на b;
в) прирост дохода, если одновременно выполняется а) и б);
г) равновесный доход, если автономные расходы равны а.
8. При росте национального дохода с 30 до 40 потребление в обществе возросло с 23 до 30. Имеется высокая безработица, а уровень цен неизменен. Найти:
а) предельную склонность к потреблению;
б) предельную склонность к сбережению;
в) простой мультипликатор;
г) изменение национального дохода, если инвестиции сократились на 2.
9. Предельная склонность к потреблению равна MPC = 0,8, предельная налоговая ставка равна t = 0,3. Инвестиции в экономике увеличились на 3 млрд руб. Найти:
а) простой мультипликатор;
б) сложный мультипликатор;
в) прирост национального дохода;
г) прирост налоговых поступлений в бюджет;
д) прирост национального дохода, если предельная склонность к потреблению снизится до 0,7;
е) прирост национального дохода, если предельная налоговая ставка увеличится до 0,5. Сделайте вывод.
Похожие работы
... Дж. М. Кейнс (1883 - 1946). Его учение направлено против идей классической экономической школы, что обосновало модели свободного рыночного хозяйства как равновесной саморегулирующей системы. Макроэкономика является одной из самых молодых экономических наук. Своей зрелости она достигла в 30-ые годы ХХ ст. в период мирового экономического кризиса, когда приобрела способность влиять на экономическую ...
... ). Мы придерживаемся точки зрения, согласно которой региональная экономика является ветвью общей экономической теории, относящейся к разделу «Мезоэкономика», то есть рассматриваем региональную экономику как часть крупную подсистему национальной экономики (Макроэкономики). Курс методологически опирается на основы экономической теории и органически связан с конкретными экономическими дисциплинами, ...
... а экономико-административная (с ударением на первом слове) модель должна стать приоритетом. И изобретать тут ничего нового не приходится. Среди главных и апробированных инструментов регулирования рыночной экономики следующие: финансово-кредитная система с совершенной налоговой, эмиссионной и таможенно-пошлинной политикой, финансированием, кредитом, стратегией и тактикой процентных ставок; ...
тологией, социологией и другими общественными дисциплинами. Это не может не породить трудностей - указанные дисциплины оперируют преимущественно качественными категориями, а в основу макроэкономики как уже отмечалось, положены также и количественные исследования. Поэтому необходимы специальные методы анализа и, в частности, моделирования переходных экономических процессов. В условиях переходного ...
0 комментариев