Прямоугольный треугольник

2.5 Прямоугольный треугольник

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой:

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы:

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c² =a² + b²

 

3. Практическая часть

 

3.1 Задачи с окружностью, описанной около треугольника

 

Задача 1: Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O. Найдите ее радиус, если площадь треугольника BOC равна 16.

 

 

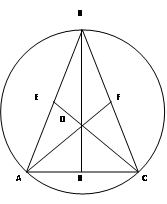
Дано: ∆ ABC – равнобедренный, AC – основание, ﮮ ACB = 75˚,

площадь ∆ BOC равна 16

Найти: радиус описанной окружности

Решение:

1.  Проведем медианы AF, CE, BH

2.  ∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный

3.  ﮮ HBC = 90˚ - ﮮ ACB, ﮮ HBC = 90˚ - 75˚ = 15˚

4.  BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚

5.  ﮮ COB = 180˚ - (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ - (15˚ + 15˚) = 150˚

6.  S =  ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника), S_BOC =  ∙ R ∙ R ∙ sin 150˚ =  ∙ R ∙ R ∙  =  ∙ R² ;  ∙ R² = 16; R² = 16 :  = 64; R =  = 8

Ответ: R = 8

 

Задача 2: треугольник BMP с углом B, равным 45˚, вписан в окружность радиуса 6. Найдите длину медианы BK, если BK пересекает окружность в точке C и CK = 3.

 

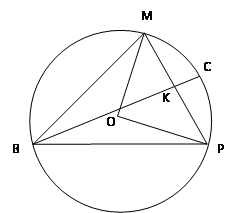
Решение:

1.  ﮮ MOP = 2 ﮮMBP

ﮮ MOP = 2 ∙ 45˚ = 90˚, следовательно, ∆ MOP – прямоугольный

2.  MP² = OM² + OP²

MP² = 6² + 6² = 36 + 36 = 36 ∙ 2

MP =

3.  MK = KP = 0,5 ∙ MP

MK = KP = 0,5 ∙  =

4.  MK ∙ KP = BK ∙ KC

 = BK ∙ 3

BK ∙ 3 = 9 ∙ 2

BK ∙ 3 = 18

BK = 6

Ответ: BK = 6

Задача 3: остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.

 

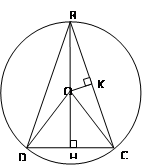
Решение:

1.  ∆ BCD – равнобедренный, CD = 16, следовательно, DH = HC = 8

2.  ∆ DOH – прямоугольный

По теореме Пифагора:

OH² = 10² – 8²

OH² = 100 – 64 = 36

OH = 6

3.  BH = BO + OH = 10 + 6 =16

4.  По теореме Пифагора:

BC² = 16² + 8² = 256 + 64 = 320

BC =

5.  ∆ KBO ~ ∆ HBC

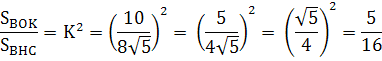
6.  S_BHC =  

7. 

S_BOK = 20

8.  S_BOC = 2 ∙ S_BOK = 2 ∙ 20 = 40

Ответ: S_BOC = 40

 

3.2 Задачи с окружностью, вписанной в треугольник

 

Задача 4: радиус окружности, вписанной в прямоугольный треугольник, равен 2 м, а радиус описанной окружности равен 5 м. Найдите больший катет треугольника.

 

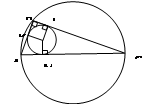
Решение:

1.  AC = 2r = 10 м

2.  Пусть AM = AK = x, MC = CL = y

По теореме Пифагора:

x + y = 10

(x + 2)² + (y + 2)² = (x + y)²

y = 10 – x

(x + 2)² + (10 – x + 2)² = (x + 10 – x)²

(x + 2)² + (12 – x)² = 100

x² + 4x + 4 +144 – 24x + x² = 100

2x² – 20x + 148 = 100

2x² – 20x + 48 = 0

x² – 10x + 24 = 0

x₁ = 6, x₂ = 4

 y = 10 – x

x = 6 x = 4

y = 4 y = 6

3. Так как нужно найти больший катет, то берем y = 6

BC = 2 + 6 = 8 м

Ответ: BС = 8 м

Задача 5: окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.

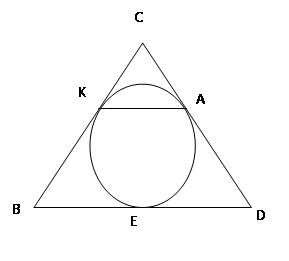
Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10

Найти: KA

Решение:

1.  CD = CB = BK + KC, CD = CB = 15 + 10 = 25

2.  CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD – CA, AD = 25 – 10 = 15

3.  BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30

4.  ∆ CKA ~ ∆ CBD (ﮮC – общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12

Ответ: KA = 12

 

1.  BC = x + y

BC = 18 + 12 = 30 (м)

Ответ: 30 м – диаметр описанной окружности

 

 

3.3. Задачи с окружностью, описанной около четырехугольника

 

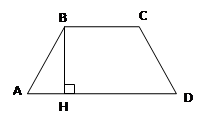
Задача 6: в равнобедренной трапеции основания 21 и 9 сантиметров, высота – 8 сантиметров. Найти радиус описанной окружности.

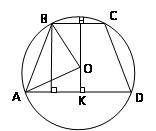
Решение:

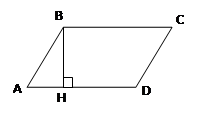
1.  Проведем серединные перпендикуляры к основаниям Н и К, тогда центр окружности О лежит на прямой НК.

2.  АО=ОВ=R. Точка О делит отрезок НК на две части: пусть НО = х, тогда ОК = 8 – х.

3.  АО² = АК² + КО²; ОВ² = ВН² + НО²;

так как ОА²=ОВ², получим:

АК² + КО² = ВН² + НО²

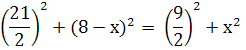
90 + 64 – 16x = 0

16x = 154

ОВ² = ВН² + НО²

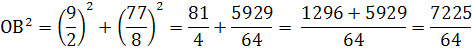
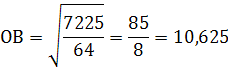
Ответ: OB = 10,625