Навигация
Вычисление средней арифметической по исходным данным
4. Вычисление средней арифметической по исходным данным.
Для расчета применяется формула средней арифметической простой:
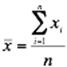
![]() = 7423/30 = 247,43 тыс. руб./чел.
= 7423/30 = 247,43 тыс. руб./чел.
Причина расхождения средних величин, рассчитанных по исходным данным (247,43 тыс. руб./чел.) и по интервальному ряду распределения (248 тыс. руб./чел.), заключается в том, что в первом случае средняя определяется по фактическим значениям исследуемого признака для всех 30-ти организациях, а во втором случае в качестве значений признака берутся середины интервалов и, следовательно, значение средней будет менее точным.
Задание 2.
По исходным данным (табл. 2.1) с использованием результатов выполнения Задания 1 необходимо выполнить следующее:
1. Установить наличие и характер корреляционной связи между признаками — среднесписочная численность работников и уровень производительности труда, образовав по каждому признаку пять групп с равными интервалами, используя методы:
а) аналитической группировки;
б) корреляционной таблицы.
2. Оценить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения Задания 2.
Выполнение Задания 2.
Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, а также установление направления связи и оценка ее тесноты.
По условию Задания 2 факторным является признак Среднесписочная численность менеджеров, результативным – признак Объем продаж.
1. Установление наличия и характера связи между признаками - среднесписочная численность работников и уровень производительности труда методами аналитической группировки и корреляционной таблицы
Применение метода аналитической группировки.
Аналитическая группировка строится по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х – уровень производительности труда и результативным признаком Y –среднесписочная численность работников. Построенную аналитическую группировку представляем в табл. 2.7:
Таблица 2.7
Зависимость уровня производительности труда от среднесписочной численности работников
| Номер группы | Группы организаций по уровню производительности труда, тыс. руб./чел., х | Число организаций, fj | Среднесписочная численность работников, чел. | |
| Всего | В среднем на одну организацию, | |||
| 1 | 120 — 168 | 3 | 406 | 135,33 |
| 2 | 168 — 216 | 4 | 634 | 158,5 |
| 3 | 216 — 264 | 12 | 1980 | 165 |
| 4 | 264 — 312 | 7 | 1330 | 190 |
| 5 | 312 — 360 | 4 | 840 | 210 |
| Итого: | 30 | 5190 | 858,83 | |
Вывод. Анализ данных табл. 2.6 показывает, что с увеличением показателя производительности труда от группы к группе систематически возрастает и среднесписочная численность работников по каждой группе организаций, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.
Применение метода корреляционной таблицы.
Корреляционная таблица строится как комбинация двух рядов распределения по факторному признаку Х и результативному признаку Y. На пересечении j-ой строки и k-ой графы таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый интервал по признаку Y. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками - прямой или обратной. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему, обратная - по диагонали от правого верхнего угла к левому нижнему.
Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Величина интервала и границы интервалов для факторного признака Х – уровень производительности труда известны из табл. 4. Определим величину интервала для результативного признака Y – среднесписочная численность работников ( при k = 5, уmax= 220 чел., уmin= 120 чел.:
h = (220-120)/5 = 20 чел.
Границы интервалов ряда распределения результативного признака Y имеют следующий вид (табл. 2.8):
Таблица 2.8
| Номер группы | Нижняя граница, чел. | Верхняя граница, чел. |
| 1 | 120 | 140 |
| 2 | 140 | 160 |
| 3 | 160 | 180 |
| 4 | 180 | 200 |
| 5 | 200 | 220 |
Подсчитывая с использованием принципа полуоткрытого интервала число организаций, входящих в каждую группу (частоты групп), получаем интервальный ряд распределения результативного признака (табл. 2.9).
Таблица 2.9
Интервальный ряд распределения организаций по среднесписочной численности работников
| Номер группы | Группы организаций по среднесписочной численности работников, чел., x | Число организаций, fj |
| 1 | 120-140 | 2 |
| 2 | 140-160 | 5 |
| 3 | 160-180 | 12 |
| 4 | 180-200 | 7 |
| 5 | 200-220 | 4 |
| ИТОГО: | 30 |
Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 2.10).
Таблица 2.10
Корреляционная таблица зависимости уровня производительности труда от среднесписочной численности работников
| Группы организаций по уровню производительности труда, тыс. руб./чел. | Группы организаций по среднесписочной численности работников, чел. | |||||
| 120-140 | 140-160 | 160-180 | 180-200 | 200-220 | Итого | |
| 120 — 168 | 2 | 1 | 3 | |||
| 168 — 216 | 4 | 4 | ||||
| 216 — 264 | 12 | 12 | ||||
| 264 — 312 | 7 | 7 | ||||
| 312 — 360 | 4 | 4 | ||||
| Итого | 2 | 5 | 12 | 7 | 4 | 30 |
Вывод. Анализ данных табл. 2.10 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между уровнем производительности труда и среднесписочной численностью работников.
1.Измерение тесноты корреляционной связи с использованием коэффициента детерминации η2 и эмпирического корреляционного отношения η.
Коэффициент детерминации η2 характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
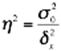 , где
, где
![]() – общая дисперсия признака Y,
– общая дисперсия признака Y,
![]() – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Общая дисперсия характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле
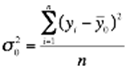 , где
, где
yi – индивидуальные значения результативного признака;
![]() – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.Расчет общей дисперсии по формуле :
Межгрупповая дисперсия измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних от общей средней . Показатель вычисляется по формуле:
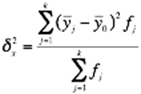 , где
, где
![]() – групповые средние,
– групповые средние,
![]() – общая средняя,
– общая средняя,
fj – число единиц в j-ой группе,
k – число групп.
Для расчета показателей и необходимо знать величину общей средней, которая вычисляется как средняя арифметическая простая по всем единицам совокупности:
y0 = 5190/30 = 173 чел.
Для расчета общей дисперсии применяется вспомогательная таблица :
Таблица 2.11
Вспомогательная таблица для расчета общей дисперсии
| Номер организации п/п | Среднесписочная численность работников, чел. |
|
|
|
| 1 | 162 | -11 | 121 | 26244 |
| 2 | 156 | -17 | 289 | 24336 |
| 3 | 179 | 6 | 36 | 32041 |
| 4 | 194 | 21 | 441 | 37636 |
| 5 | 165 | -8 | 64 | 27225 |
| 6 | 158 | -15 | 225 | 24964 |
| 7 | 220 | 47 | 2209 | 48400 |
| 8 | 190 | 17 | 289 | 36100 |
| 9 | 163 | -10 | 100 | 26569 |
| 10 | 159 | -14 | 196 | 25281 |
| 11 | 167 | -6 | 36 | 27889 |
| 12 | 205 | 32 | 1024 | 42025 |
| 13 | 187 | 14 | 196 | 34969 |
| 14 | 161 | -12 | 144 | 25921 |
| 15 | 120 | -53 | 2809 | 14400 |
| 16 | 162 | -11 | 121 | 26244 |
| 17 | 188 | 15 | 225 | 35344 |
| 18 | 164 | -9 | 81 | 26896 |
| 19 | 192 | 19 | 361 | 36864 |
| 20 | 130 | -43 | 1849 | 16900 |
| 21 | 159 | -14 | 196 | 25281 |
| 22 | 162 | -11 | 121 | 26244 |
| 23 | 193 | 20 | 400 | 37249 |
| 24 | 158 | -15 | 225 | 24964 |
| 25 | 168 | -5 | 25 | 28224 |
| 26 | 208 | 35 | 1225 | 43264 |
| 27 | 166 | -7 | 49 | 27556 |
| 28 | 207 | 34 | 1156 | 42849 |
| 29 | 161 | -12 | 144 | 25921 |
| 30 | 186 | 13 | 169 | 34596 |
| Итого: | 5190 | 14526 | 912396 |
Рассчитаем общую дисперсию:
![]() =14526/30 = 484,2
=14526/30 = 484,2
Для расчета межгрупповой дисперсии строится вспомогательная таблица:
Таблица 2.12
Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы организаций по уровню производительности труда, тыс. руб./чел. | Число организаций, fj | Среднее значение | |
|
| 120 — 168 | 3 | 135,33 | -37,67 | 4257,0867 |
| 168 — 216 | 4 | 158,5 | -14,5 | 841 |
| 216 — 264 | 12 | 165 | -8 | 768 |
| 264 — 312 | 7 | 190 | 17 | 2023 |
| 312 — 360 | 4 | 210 | 37 | 5476 |
| Итого: | 30 | 13365,0867 |
![]() = 13365,0867/30 = 445,5
= 13365,0867/30 = 445,5
Определяем коэффициент детерминации:
η2 = 445,5/484,2 = 0,9201 или 92,01%
Вывод. 92,01% вариации суммы среднесписочной численности работников обусловлено вариацией объема уровня производительности труда, а 7,99% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение η оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
η = √η2 = √ 0,9201 = 0,9592 или 95,92 %
Вывод. Согласно шкале Чэддока связь между уровнем производи-тельности труда и среднесписочной численностью работников является весьма тесной.
Задание 3.
По результатам выполнения Задания 1 с вероятностью 0,683 необходимо определить:
1) ошибку выборки среднего уровня производительности труда и границы, в которых будет находиться генеральная средняя.
2) ошибку выборки доли организаций с уровнем производительности труда 264 тыс. руб./чел. и более, а также границы, в которых будет находиться генеральная доля.
Целью выполнения данного Задания является определение для генеральной совокупности организаций границ, в которых будут находиться средняя величина производительности труда, и доля организаций с уровнем производительнотси труда 264 тыс. руб./чел.
Похожие работы
... план по договорным обязательствам, по объему перевозок, по номенклатуре грузов. Чем ближе значение показателя к 100%, тем ритмичнее работа автотранспортного предприятия, коэффициент ритмичности на рассматриваемом предприятии 100,46. 3. Статистическое изучение основного капитала По данным бухгалтерского учета стоимость основного капитала и его элементов известна по состоянию на начало и ...
... в результате изменения объема основных фондов и фондоотдачи осуществляется на основе индексов стоимостного объема производства, основных фондов и индекса фондоотдачи. 3. Применение балансового метода в изучении основных фондов 3.1 Статистические методы, используемые в изучении ОФ Основными методами являются сводка и группировка, обобщающие статистические показатели (выраженные абсолютными, ...
... , переуступкой прав собственности, взаимным зачетом требований, по прямому товарообмену (бартеру), прочими видами расчетов. На основе статистического наблюдения формируются базовые показатели статистики финансов предприятий, характеризующие финансовые результаты их деятельности, главными из которых являются выручка от продаж и прибыль. На основе базовых показателей определяются производные ( ...
... показателей эффективности использования фондов снизился на 9,5%; 14. Уровень рентабельности вырос на 0,6%; 15. норма рентабельности снизилась на 28,6%. Глава 3 Статистический анализ трудовых ресурсов 3.1 Статистический анализ и использование трудовых ресурсов в Райпо Трудовые ресурсы – это часть населения обоего пола в трудоспособном возрасте за вычетом неработающих, нетрудоспособных и ...


0 комментариев