Навигация
Інтегральні перетворення Лапласа
Вступ
В багатьох задачах математичного аналізу розглядаються випадки, в яких кожна точка одного простору ставиться у відповідність деякій точці іншого (або того ж самого) простору. Відповідність між двома точками встановлюється за допомогою перетворення або оператора. В задачу теорії операторів входить докладний опис і класифікація різноманітних видів перетворень і їх властивостей, а також розробка символічних методів, що дозволяють мінімалізувати і спростити обчислення. Застосування операційного метода можна порівняти з логарифмуванням, коли 1) від чисел переходять до логарифмів, 2) над логарифмами проводять дії, що відповідають діям над числами, при тому множенню чисел відповідає більш проста операція складання логарифмів і т.д. 3) від найденого логарифма знов повертаються до числа. В операційному методі широко використовується перетворення Лапласа, яке перетворює певний клас функцій-оригіналів f(t) дійсної змінної t в функцію-зображення F(p) комплексної змінної p.
1. Означення перетворення Лапласа. Оригінал і зображення.
Нехай f [ t] -інтегрована на (0,Т) при довільному Т>0 функція, що дорівнює нулю при t>0 : f[t]=0 при t<0. Якщо ця функція при t>0 задовольняє оцінці:
![]() (1.1)
(1.1)
то можна розглянути інтеграл
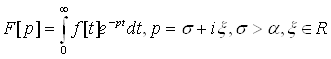 (1.2)
(1.2)
Дійсно справджується оцінка
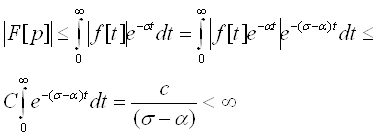 (1.3)
(1.3)
При виведенні (1.3) була застосована оцінка (1.1). З оцінки (1.3), зокрема, випливає, що ![]() . Функція
. Функція ![]() є аналітичною функцією комплексної змінної
є аналітичною функцією комплексної змінної ![]() в півплощині
в півплощині ![]() . Для того щоб це перевірити, знаходимо поки формально:
. Для того щоб це перевірити, знаходимо поки формально:
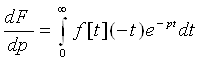 (1.4)
(1.4)
Як і при виведенні (1.3), знаходимо
 (1.5)
(1.5)
Останнє означає що інтеграл рівномірно по Rep>a збігається і випливає що похідна ![]() існує при
існує при ![]() , і формула (1.4) справедлива при
, і формула (1.4) справедлива при ![]() .
.
Інтеграл (1.2) називається перетворенням Лапласа функції ![]() і позначається -
і позначається -![]() . В цьому випадку функція
. В цьому випадку функція ![]() називається оригіналом, а функція
називається оригіналом, а функція ![]() – зображенням.
– зображенням.
Перетворення Лапласа можна зв’язати з перетворенням Фур’є. Дійсно з (1.2) маємо:
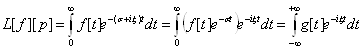
Де ![]() (Перетворення Фур’є із знаком «-»)
(Перетворення Фур’є із знаком «-»)
2. Властивості перетворення Лапласа L
Лінійність.
![]()
Доведення:
В силу властивостей інтеграла:

Диференціювання зображення
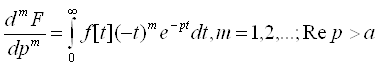
Для m=1 властивість вже встановлено. Для довільного m властивість доводиться аналогічно.
Перетворення Лапласа похідних.
![]()
Для m=1 за допомогою інтегрування частинами знаходимо

При цьому ми врахували, що виконуються наступні оцінки:
![]()
При ![]()
![]() и
и ![]() . Для довільного m властивість 2.3 встановлюється за індукцією
. Для довільного m властивість 2.3 встановлюється за індукцією
Зсув перетворення Лапласа.
![]()
Доведення властивості 2.4 очевидно.
Перетворення Лапласа і його подібності.
![]()
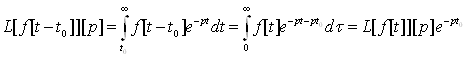
Зсув оригінала в перетворенні Лапласа.

Доведення. Позначимо
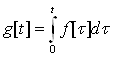
Очевидно, що g’[t]=f[t], g[+0]=0
Тому за допомогою інтегрування частинами знаходимо
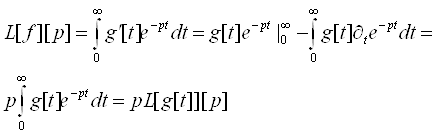
При цьому ми врахували що g[+0]=0 в силу умови (1.1)

при ![]() ,
, ![]() ,
, ![]() .
.
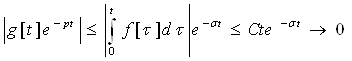
при ![]() ,
, ![]() ,
, ![]() .
.
Звідси знаходимо
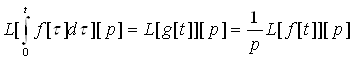
Перетворення Лапласа дробу f[t]/t.
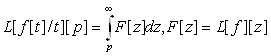
Доведення. Позначив Ф[p]=£[f[t]\t][p] . Знайдемо
![]()
Останню рівність про інтегруємо по довільному шляху від р до довільної точки z=Rez=∞
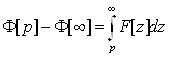
Враховуючи, що в силу (1.3) Ф[∞]=0. І отримаємо потрібну властивість (2.8).
Перетворення Лапласа згортки f*g.
![]()
Доведення. Позначимо

Очевидно, що ![]() при t→∞
при t→∞
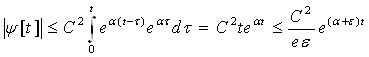
При довільному έ>0. Для доведення останньої нерівності ми використовуємо також оцінку.
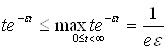
Звідси при ![]()
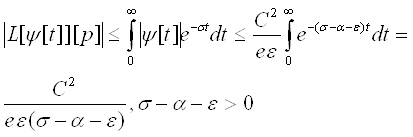
Таким чином, при Rep>a

Тут ми скористалися теоремою Фуббіні і змінили порядок інтегрування.
Похожие работы
... ів у буферний ЗП контролера клавіатури та дисплея. Але під час виконання роботи був знайдений більш ефективний метод для аналізу пульсової хвилі – вейвлет-аналіз, якому і присвячений наступний розділ. 3. СУТНІСТЬ ВЕЙВЛЕТ-АНАЛІЗУ Вейвлет-перетвореня сигналів є узагальненням спектрального аналізу, типовий представник якого - класичне перетворення Фур'є. Застосовувані для цієї мети базиси ...
... детально на основі загального вирішення задачі.ЗАВДАННЯ ДО КУРСОВОЇ РОБОТИ Розробити компоненти технічного і програмного забезпечення мікропроцесорного пристрою, який включає аналогово-цифровий і цифро-аналоговий перетворювачі і виконує функцію лінійної системи автоматизованого регулювання. Системи описується заданим пропорційно-інтегро-диференціальним рівнянням, яке зв'язує аналогові сигнали х ...
... і фільтрації по просторових координатах. 1.1.3. Моделювання масопереносу у випадку D=D( ) при наявності масообміну Вихідні рівняння. Процес масопереносу розчинних речовин (солей, гіпсів й ін.) при фільтрації підземних вод можна описати наступною системою диференціальних рівнянь у частинних похідних: (1.84) (1.85) (1.86) де - вектор швидкості фільтрації; - ...
... (10), одержимо: ; ; . Звідси, зокрема, треба, що . Використовуючи (11), одержимо: ; ; . По членне додавання й вирахування отриманих рівностей дає: , (12) . (13) Формула (13) дозволяє виразити всі Беселеві функції із цілими індексами через , . Дійсно, з (13) знаходимо (думаючи ): , (13`) звідки послідовно одержуємо: , , ………………… 3. Беселеві функції з напівцілим і ...


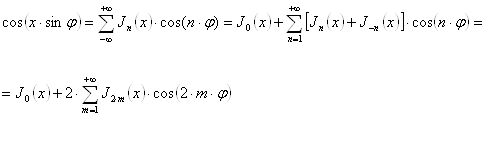
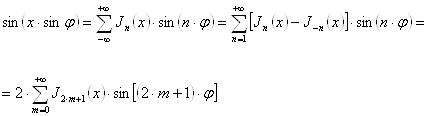

0 комментариев