Навигация
Обчислення перетворення Лапласа основних функцій
3. Обчислення перетворення Лапласа основних функцій
1. f[t]=e![]() . Rep>Reλ, λ
. Rep>Reλ, λ![]()
![]()
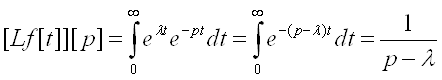
2. f[t]=Sin[ωt], ω![]() R
R
За формулами Ейлера маємо
Sin[ωt]=![]()
Тому за допомогою 1 маємо:

3. f[t]=cos[ωt], ω![]() L[cos[ωt]][p]=
L[cos[ωt]][p]=![]()
Доведення аналогічне.
4. f[t]=Sh[ωt], ω![]() R
R
За означенням гіперболічних функцій Sh[ωt]= ![]() /2
/2
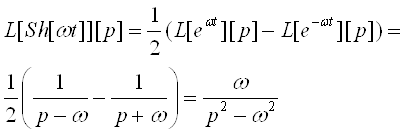
5. ![]()
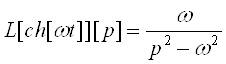
Доведення аналогічне.
6. ![]()
За властивістю 2.2 маємо:
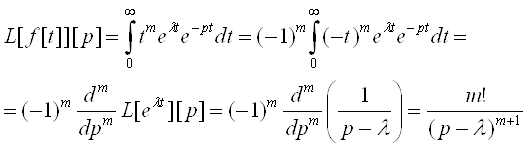
Зокрема
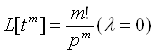
7. ![]()
![]()
Як і у прикладі 6, знаходимо для функції ![]()
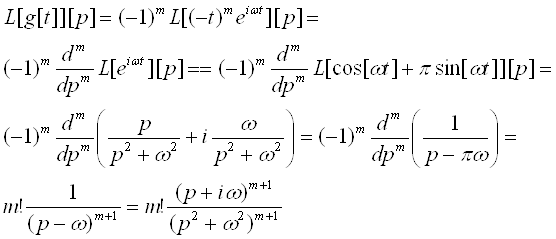
Застосуємо далі для лівої і правої частини отриманої рівності операції дійсної уявної частини, вважаючи р дійсним і додатнім.
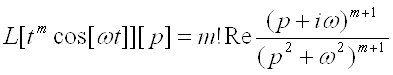 (3.1)
(3.1)
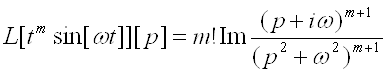 (3.2)
(3.2)
4. Обернене перетворення Лапласа
Теорема 4.1 (основна) Нехай функція f(t) задовольняє умові (1.1) і F(p) її зображення. Тоді в довільній точці t>0 в якої функція f(t) диференційована, справджується формула подання:
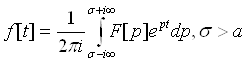 (4.1)
(4.1)
Доведення
Розглянемо функцію ![]() . Очевидно, що функція g[t] інтегрована на (0,∞) і диференційована в т. t>0. Розглядаючи F[p] перетворення Фур’є функції g[t] обернення перетворення Фур’є.
. Очевидно, що функція g[t] інтегрована на (0,∞) і диференційована в т. t>0. Розглядаючи F[p] перетворення Фур’є функції g[t] обернення перетворення Фур’є.
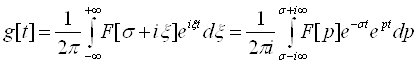
Після множення останньої рівності на ![]() отримаємо 4.1. 4.1 називається формулою оберненого перетворення Лапласа або формулою Мелліна. Теорему доведено. ■
отримаємо 4.1. 4.1 називається формулою оберненого перетворення Лапласа або формулою Мелліна. Теорему доведено. ■
Теорема має недолік, для її застосування необхідно попередньо володіти інформацією про властивості вихідного оригінала f[t]. В наступній теоремі встановлюється формула звертання при достатніх умовах тільки на зображення F[p].
Теорема 4.2 Нехай F[p] аналітична на півплощині Rep>a що задовольняє умовам:
1) При будь-якому ![]() існує інтеграл:
існує інтеграл:
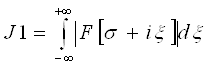
2) Для
![]()
- дуги кола радіуса R з центром в точці (![]() ,0)
,0)
![]() , при
, при ![]()
Тоді, ![]() - це зображення функції f[t], представленої формулою 4.1 (
- це зображення функції f[t], представленої формулою 4.1 (![]() )
)
Доведення
Розглянемо прямокутний контур ![]() (мал..4.1)
(мал..4.1)
За теоремою Коши інтеграл Г[σ1, σ2, р] по контуру J1[σ1, σ2, р] дорівнює нулю. Перейдемо до границі в J1[σ1, σ2, р] при р→∞. Легко переконатися, що інтеграли за верхній і нижній сторонам прямокутника прямують до 0 при р→∞, а інтеграли по бічним сторонам в границі виявляються рівними за величиною. Таким чином, інтеграл (4.1) не залежить від вибору ![]() .
.
Доведемо, що побудована за формулою (4.1) функція f[t] дійсно є оригіналом заданої функції F[p]. Перш за все зауважимо, що для інтеграла (4.1) справедлива оцінка
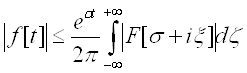
Звідси випливає, що інтеграл (4.1) рівномірно по ![]() збігається.
збігається.
Доведемо, що f[t]=0, при t<0. Для цього розглянемо інтеграл ![]() по замкненому контуру
по замкненому контуру ![]() в півплощині
в півплощині ![]() , що складається з дуги кола
, що складається з дуги кола ![]() радіуса R і відрізка прямої (мал. 4.2). За теоремою Коши :
радіуса R і відрізка прямої (мал. 4.2). За теоремою Коши :
![]()
В силу леми Жордана інтеграл по дузі кола прямує до нуля при t<0 і R→∞. Інтеграл що залишився в границі переходить до інтегралу по прямій ![]() , дорівнює нулю при t<0. Покажемо нарешті що перетворення Лапласа в точці p=q(
, дорівнює нулю при t<0. Покажемо нарешті що перетворення Лапласа в точці p=q(![]() ) співпадає з F[q]. За допомогою формули Коши знаходимо при
) співпадає з F[q]. За допомогою формули Коши знаходимо при ![]()
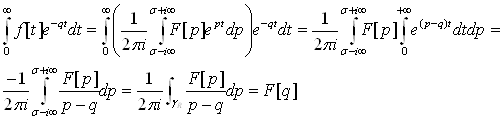 ■
■
При виведенні ми врахували що інтеграл по прямій можна замінити на інтеграл за замкненим контуром ![]() , так як
, так як
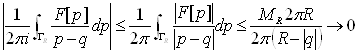 при R→∞
при R→∞
Лема Жордана. Нехай t>0 і ![]() - півколо радіуса R в півплощині
- півколо радіуса R в півплощині ![]() . Якщо функція
. Якщо функція ![]() задовольняє умовам:
задовольняє умовам:
![]() функція
функція ![]() неперервна при
неперервна при ![]() ,
, ![]() ,
,![]()
![]()
![]()
Тоді ![]() при R→∞
при R→∞
Доведення
Зробимо заміну змінної інтегрування
z=R![]()
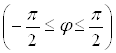 .
.
Тоді справедлива оцінка інтеграла

Як відомо, при ![]()
![]() . Продовжимо оцінку інтеграла
. Продовжимо оцінку інтеграла
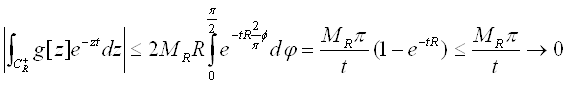
При R→∞. Лему доведено■
Задача Знайти перетворення Лапласа функції ![]()
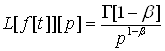 (5.1)
(5.1)
Введена гамма-функція
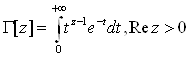
Розглянемо спочатку L[f[t]][p] при p>0. За допомогою простої заміни змінних знаходимо
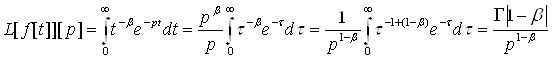
Нехай далі ![]() і
і ![]() . Для визначеності будемо вважати
. Для визначеності будемо вважати ![]() ,
, ![]() (випадок
(випадок ![]() розглядається аналогічно). Покладемо
розглядається аналогічно). Покладемо ![]() . Легко перевіряється що ps=t – додатне число.
. Легко перевіряється що ps=t – додатне число.
Далі маємо:
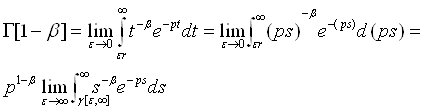 (5.2)
(5.2)
де ![]() - відрізок променя
- відрізок променя ![]() . Побудуємо замкнений контур
. Побудуємо замкнений контур ![]() (мал. 5.1). За теоремою Коши:
(мал. 5.1). За теоремою Коши:
![]()
Оцінимо інтеграл по дузі ![]() і кола радіуса R
і кола радіуса R
![]()
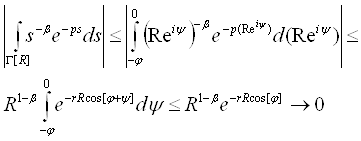
при R→∞.
Перейдемо до границі при R→∞, ![]() →0 в рівності (5.3), отримуємо
→0 в рівності (5.3), отримуємо
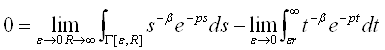
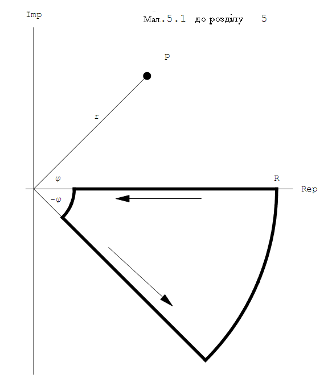
Звідси і із 5.2 встановлюємо (5.1).
Похожие работы
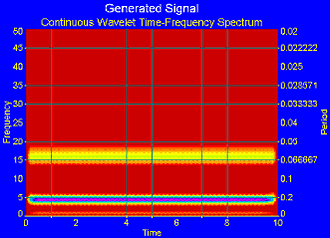
... ів у буферний ЗП контролера клавіатури та дисплея. Але під час виконання роботи був знайдений більш ефективний метод для аналізу пульсової хвилі – вейвлет-аналіз, якому і присвячений наступний розділ. 3. СУТНІСТЬ ВЕЙВЛЕТ-АНАЛІЗУ Вейвлет-перетвореня сигналів є узагальненням спектрального аналізу, типовий представник якого - класичне перетворення Фур'є. Застосовувані для цієї мети базиси ...
... детально на основі загального вирішення задачі.ЗАВДАННЯ ДО КУРСОВОЇ РОБОТИ Розробити компоненти технічного і програмного забезпечення мікропроцесорного пристрою, який включає аналогово-цифровий і цифро-аналоговий перетворювачі і виконує функцію лінійної системи автоматизованого регулювання. Системи описується заданим пропорційно-інтегро-диференціальним рівнянням, яке зв'язує аналогові сигнали х ...
... і фільтрації по просторових координатах. 1.1.3. Моделювання масопереносу у випадку D=D( ) при наявності масообміну Вихідні рівняння. Процес масопереносу розчинних речовин (солей, гіпсів й ін.) при фільтрації підземних вод можна описати наступною системою диференціальних рівнянь у частинних похідних: (1.84) (1.85) (1.86) де - вектор швидкості фільтрації; - ...
... (10), одержимо: ; ; . Звідси, зокрема, треба, що . Використовуючи (11), одержимо: ; ; . По членне додавання й вирахування отриманих рівностей дає: , (12) . (13) Формула (13) дозволяє виразити всі Беселеві функції із цілими індексами через , . Дійсно, з (13) знаходимо (думаючи ): , (13`) звідки послідовно одержуємо: , , ………………… 3. Беселеві функції з напівцілим і ...


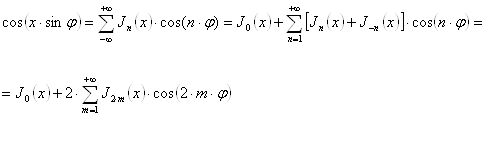
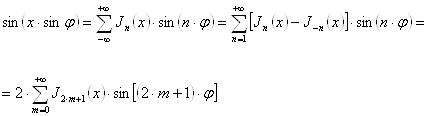

0 комментариев