Навигация
Приклади розв’язання базових задач
9485
знаков
1
таблица
11
изображений
5. Приклади розв’язання базових задач
Зауваження. Функцією-оригіналом називається будь-яка комплексно значна функція f(t) дійсного аргументу t, що задовольняє умовам:
1°. f(t) інтегрована на будь-якому скінченому інтервалі вісі t (локально інтегрована).
2°.Для усіх від’ємних t
3°. f(t) зростає не швидше ніж показникові функція, тобто існують такі сталі 
і 
, що для усіх t
Задача1. Показати що функція є функцією-оригіналом.
|
|
|
|
Розв’язання
Дійсно, функція f(t)локально інтегрована
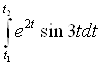
існує для будь-яких скінчених 
і 
. Умова 2° виконана в силу завдання функції.
І врешті решт, для будь-яких дійсних 
,
Тобто в якості М в умові 3° можна вибрати довільне число >1 
Задача2. Користуючись означенням, знайти означення функції
Розв’язання
Для функції маємо . Тому зображення 
буде в усякому разі визначене і аналітичне на півплощині 
. Маємо:
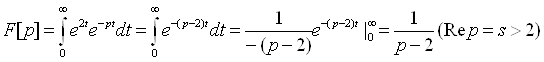
Тобто, 
. Ця функція аналітична при , і крім того вона аналітична всюди, за виключенням точки 
. Це не суперечить означенню, так як останнє гарантує аналітичність при 
, але не стверджує, що якщо 
, тоді функція буде всюди аналітична.
Задача3. Знайти зображення функції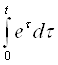 
Розв’язання
Маємо 
. За теоремою про інтегрування оригінала
Задача4. 
Розв’язання
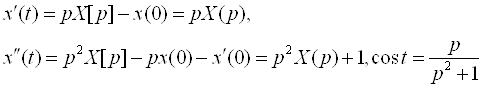
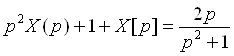
Знаходимо оригінал для функції 
Для знаходження оригіналу для функції 
скористаємось, наприклад. Теоремою про диференціювання зображення.
Отже, 
Тобто, 
Висновок
Застосування методів, що використовують перетворення Лапласа знайшло широке застосування в розв’язанні різноманітних задач електротехніки, гідродинаміки, механіки, радіотехніки, а також і ряду інших областей науки та техніки, тому що воно дозволяє мінімалізувати і спростити обчислення складних задач диференціальних рівнянь, рівнянь в частинних похідних, інтегро-диференціальних рівнянь типу згортки. Зокрема, в силу властивості лінійності перетворення Лапласа і його означення розв’язання звичайного лінійного диференціального рівняння з постійними коефіцієнтами задовільнє алгебричному рівнянню першого ступеня, а отже може бути легко знайдено.
Список літератури
1. Владимиров В.С. Уравнения математической физики / В.С. Владимиров-М.:Наука, 1988.-512 с.
2. Свешников А.Г. Теория функций комплексной переменной / А.Г. Свешников, А.Н. Тихонов. - М.: Наука, 1970. – 304с.
3. Сидоров Ю.В. Лекции по теории функцій комплексного переменного / Ю.В. Сидоров М.В. Федорюк М.И. Шабунин; под ред. Ю.В. Сидорова. – М.: Наука, 1982. -488с
Похожие работы
... ів у буферний ЗП контролера клавіатури та дисплея. Але під час виконання роботи був знайдений більш ефективний метод для аналізу пульсової хвилі – вейвлет-аналіз, якому і присвячений наступний розділ. 3. СУТНІСТЬ ВЕЙВЛЕТ-АНАЛІЗУ Вейвлет-перетвореня сигналів є узагальненням спектрального аналізу, типовий представник якого - класичне перетворення Фур'є. Застосовувані для цієї мети базиси ...
... детально на основі загального вирішення задачі.ЗАВДАННЯ ДО КУРСОВОЇ РОБОТИ Розробити компоненти технічного і програмного забезпечення мікропроцесорного пристрою, який включає аналогово-цифровий і цифро-аналоговий перетворювачі і виконує функцію лінійної системи автоматизованого регулювання. Системи описується заданим пропорційно-інтегро-диференціальним рівнянням, яке зв'язує аналогові сигнали х ...
... і фільтрації по просторових координатах. 1.1.3. Моделювання масопереносу у випадку D=D( ) при наявності масообміну Вихідні рівняння. Процес масопереносу розчинних речовин (солей, гіпсів й ін.) при фільтрації підземних вод можна описати наступною системою диференціальних рівнянь у частинних похідних: (1.84) (1.85) (1.86) де - вектор швидкості фільтрації; - ...
... (10), одержимо: ; ; . Звідси, зокрема, треба, що . Використовуючи (11), одержимо: ; ; . По членне додавання й вирахування отриманих рівностей дає: , (12) . (13) Формула (13) дозволяє виразити всі Беселеві функції із цілими індексами через , . Дійсно, з (13) знаходимо (думаючи ): , (13`) звідки послідовно одержуємо: , , ………………… 3. Беселеві функції з напівцілим і ...
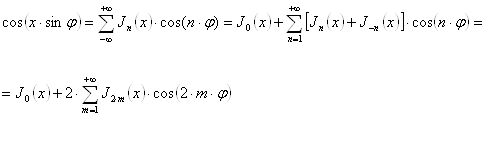
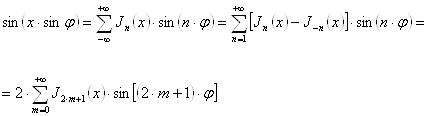
0 комментариев