Навигация
Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости
3. Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости
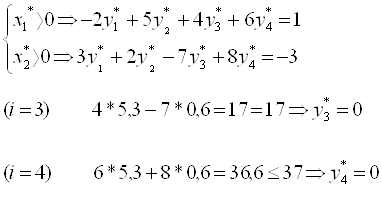
Откуда следует:
![]()
4. Оптимальный план двойственной задачи найдем, используя окончательную симплекс-таблицу прямой задачи (Табл.1)
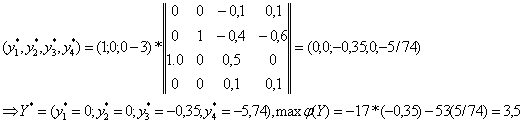
Максимальное значение функции двойственной задачи совпадает с минимальным значением функции прямой задачи, что подтверждает первую теорему двойственности.
Проанализируем решение задачи, используя условия дополняющей нежесткости (вторую теорему двойственности). Подставляем координаты оптимального решения двойственной задачи Y* = (0;0;-0,35;-0,068), в систему ограничений.
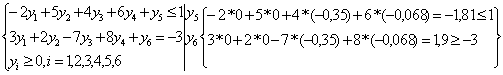
Ответ: Z(X) =3,5 при Х* = (0;0;-0,35;-0,068).
Задача № 2
Каноническая задача
В каждом варианте приведены таблицы, в которых записаны условия канонической задачи линейного программирования на минимум, т. е.
![]()
В первой строке помещены коэффициенты целевой функции. В остальных строках, в первых пяти столбцах, находятся векторы условий, а в последнем столбце записан вектор ограничений. В правом верхнем углу таблицы указана цель задачи.
Необходимо последовательно выполнить следующие задания.
1. Задачу решить графическим методом.
2. Применяя симплекс-метод, решить задачу, т.е. найти ее оптимальный план ![]() и минимальное значение целевой функции
и минимальное значение целевой функции ![]() или установить, что задача не имеет решения. Начальный план рекомендуется искать методом искусственного базиса.
или установить, что задача не имеет решения. Начальный план рекомендуется искать методом искусственного базиса.
3. Построить двойственную задачу. Если вектор ![]() найден, вычислить оптимальный план
найден, вычислить оптимальный план ![]() двойственной задачи, используя первую теорему двойственности
двойственной задачи, используя первую теорему двойственности ![]() . Вычислить максимальное значение функции
. Вычислить максимальное значение функции ![]() .
.
4. Провести анализ полученного решения, применяя условия дополняющей нежесткости.
Если ![]() , то
, то ![]() .
.
Если ![]() , то
, то ![]() .
.
| 14 | ||||||
| 1 | -5 | 6 | 8 | -2 | min | |
| 11 | 7 | 1 | 12 | 5 | 16 | |
| 14 | 10 | 0 | 3 | 8 | 17 | |
| 13 | 2 | 9 | 4 | 6 | 15 | |
Решение задачи 2
Представим исходные данные задачи в виде:
![]()
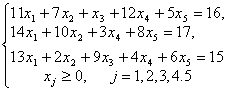
Проверяем, применим ли графический метод при решении данной задачи.
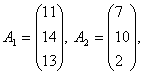
линейно независимы, так как их координаты непропорциональны. Поэтому ранг системы векторов-условий r = 3. Находим n - r =5 - 3 = 2 £ 2. Следовательно, метод применим.
1. Приведём систему уравнений-ограничений к равносильной, разрешённой методом Жордана–Гаусса. Преобразуем систему уравнений методом Жордана-Гаусса до получения общего решения (табл. 2.1).
Таблица 2.1.
| № итерац. | x1 | x2 | x3 | x4 | x5 | bi |
|
(1) | 11 | 7 | 1 | 12 | 5 | 16 |
| 14 | 10 | 0 | 3 | 8 | 17 | |
| 13 | 2 | 9 | 4 | 6 | 15 | |
(2) | -45,00 | -33,00 | 1,00 | 0,00 | -27,00 | -52,00 |
| 4,67 | 3,33 | 0,00 | 1,00 | 2,67 | 5,67 | |
| -5,67 | -11,33 | 9,00 | 0,00 | -4,67 | -7,67 | |
(3) | 2,25 | 0,75 | 1,00 | 10,13 | 0,00 | 5,38 |
| 1,75 | 1,25 | 0,00 | 0,38 | 1,00 | 2,13 | |
| 2,50 | -5,50 | 9,00 | 1,75 | 0,00 | 2,25 | |
| (4) | -12,21 | 32,57 | -51,07 | 0,00 | 0,00 | -7,64 |
| 1,21 | 2,43 | -1,93 | 0,00 | 1,00 | 1,64 | |
| 1,43 | -3,14 | 5,14 | 1,00 | 0,00 | 1,29 | |
| (5) | 0,24 | -0,64 | 1,00 | 0,00 | 0,00 | 0,15 |
| 1,68 | 1,20 | 0,00 | 0,00 | 1,00 | 1,93 | |
| 0,20 | 0,14 | 0,00 | 1,00 | 0,00 | 0,52 |
Общее решение системы уравнений имеет вид
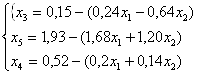
Учитывая, что все переменные неотрицательны, перейдем от уравнений к неравенствам из общего решения системы.
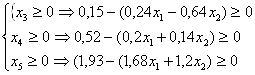
откуда получим систему неравенств с двумя переменными
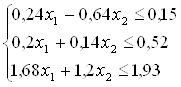
Целевую функцию выразим через свободные переменные
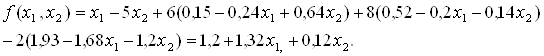
Окончательно получим стандартную задачу линейного программирования с двумя переменными
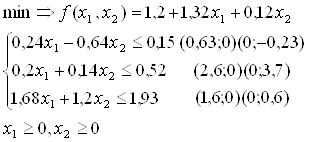
Строим область допустимых решений (график 2). Любая точка многоугольника ![]() удовлетворяет системе неравенств. Вершина
удовлетворяет системе неравенств. Вершина ![]() является точкой входа семейства прямых
является точкой входа семейства прямых ![]() в область решений, следовательно, в этой точке она принимает минимальное значение.
в область решений, следовательно, в этой точке она принимает минимальное значение.
В свою очередь, ![]() =(1,32;0,12).
=(1,32;0,12).
Решая систему уравнений получаем х1 =2,2, х2 =0,6. Это и будет оптимальным решением данной задачи, которому соответствует минимальное значение целевой функции Zmin
![]() .
.

![]()
|
![]()
|
![]() A
A
А
![]()
|
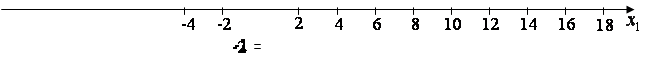 | |||
| |||
(3)
график 2
Похожие работы
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
... продукции. Кроме того, т.к. объем ресурсов для оборудования дается в часах, а производительность оборудования в м¤/час, то необходимо перейти к соизмеримости. Таким образом, задача сводится к нахождению оптимального плана производства продукции каждого вида с целью получения максимальной прибыли. ЗЛП будет выглядеть так: Целевая функция: min Z = 0.51x1+0.57x2+0.13x3+0.33x4+0.38x5+0.72x6+0.23x7+0. ...
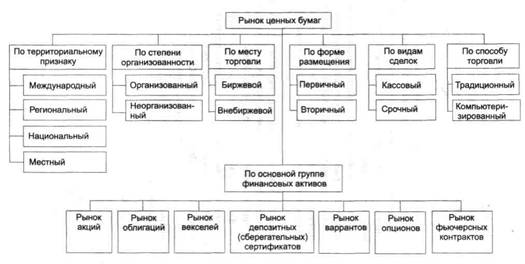
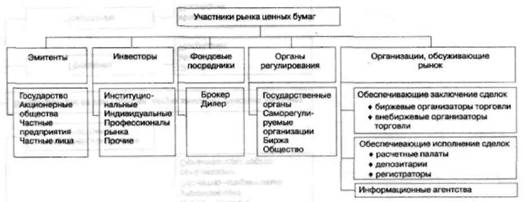
... важной составной частью как денежного рынка, так и рынка капиталов, которые в совокупности составляют финансовый рынок. Цель функционирования рынка ценных бумаг -как и всех финансовых рынков - состоит в том, чтобы обеспечивать наличие механизма для привлечения инвестиций в экономику путем установления необходимых контактов между теми, кто нуждается в средствах, и теми, кто хотел бы инвестировать ...
0 комментариев