Метод потенциалов

Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса Проанализируем решение задачи, используя условия дополняющей нежесткости (вторую теорему двойственности) Метод Фогеля Метод потенциалов Венгерский метод

38492

знака

таблиц

изображений

Метод Фогеля Читать далее: Венгерский метод

1. Метод потенциалов.

Начальный вариант выбора найдем методом максимального элемента (Табл. 5.1).

Шаг 1. Максимальным элементом является с_3,4=49. Назначим третьей невесте четвертого жениха. Вычеркнем третью строку.

Шаг 2. Из невычеркнутых элементов матрицы максимальным элементом является с_5,8=49. Назначим пятой невесте восьмого жениха. Вычеркнем пятую строку.

Шаг 3. Из невычеркнутых элементов матрицы максимальным элементом является с_6,2=49. Шестая невеста выбирает второго жениха, вычеркиваем шестую строку.

Шаг 4. Из невычеркнутых элементов матрицы максимальным элементом является с_4,3=48. Четвертая невеста выбирает третьего жениха, вычеркиваем четвертую строку.

Шаг 5. Из невычеркнутых элементов матрицы максимальным элементом является с_8,6=46. Восьмая невеста выбирает шестого жениха, вычеркиваем восьмую строку.

Шаг 6. Из невычеркнутых элементов матрицы максимальным элементом является с_7,1=45. Седьмая невеста выбирает первого жениха, вычеркиваем седьмую строку.

Шаг 7. Из невычеркнутых элементов матрицы максимальным элементом является с_1,4=41. Но четвертого жениха уже выбрала третья невеста, поэтому в клетку (1,4) поместим 0. В дальнейшем, х_1,4=0 будем считать базисной переменной. Вычеркнем четвертый столбец.

Шаг 8. Из невычеркнутых элементов матрицы максимальным элементом является с_1,7=38. Первая невеста назначается седьмому жениху, вычеркиваем первую строку.

Шаг 9. Из невычеркнутых элементов матрицы максимальным элементом является с_2,7=38. Но седьмой жених уже выбран, поэтому в клетку (2,7) поместим 0. Х_2,7=0 - базисная переменная. Вычеркнем седьмой столбец.

Шаг 10. Из невычеркнутых элементов матрицы максимальным элементом является с_2,8=36. На восьмой жених уже выбран, поэтому в клетку (2,8) поместим 0. Х_2,8=0 - базисная переменная. Вычеркнем восьмой столбец.

Шаг 11. Из невычеркнутых элементов матрицы максимальным элементом является с_2,1=35. Но первый жених уже занят, поэтому в клетку (2,1) поместим 0. Х_2,1=0 - базисная переменная. Вычеркнем первый столбец.

Шаг 12. Из невычеркнутых элементов матрицы максимальным элементом является Х_2,3=26. Но третий жених уже занят, поэтому в клетку (2,3) поместим 0. Х_2,3=0 - базисная переменная. Вычеркнем третий столбец.

Шаг 13. Из невычеркнутых элементов матрицы максимальным элементом является Х_1,5=23. Но пятый жених уже занят, поэтому в клетку (1,5) поместим 0. Х_1,5=0 - базисная переменная. Вычеркнем пятый столбец.

Шаг 14. Из невычеркнутых элементов матрицы максимальным элементом является с_2,2=20. Но второй жених уже занят, поэтому в клетку (2,2) поместим 0. Х_2,2=0 - базисная переменная. Вычеркнем второй столбец.

Шаг 15. Из невычеркнутых элементов матрицы максимальным элементом является с_2,5=17. Вторая невеста назначается пятому жениху, вычеркиваем вторую строку.

В табл. 5.1 номер шага, на котором были получены базисные переменные, указан в скобках. После 15 шага получим пробный вариант назначения Х₀: х_1,7=х_2,5= х_3,4=х_4,3=х_5,8=х_6,2= х_7,1=х_8,6=1. Это означает, что первая невеста выходит замуж за седьмого жениха, вторая невеста за пятого жениха, третья невеста за четвертого жениха, четвертая невеста за третьего жениха, пятая невеста за восьмого жениха, шестая невеста за второго жениха, седьмая невеста за первого жениха, восьмая невеста за шестого жениха.

Таблица 5.1.


31	13	11	41	10	17	38	25
			0⁽⁷⁾	0⁽¹³⁾		1⁽⁸⁾

35	20	26	8	17	14	38	36
0⁽¹¹⁾	0⁽¹⁴⁾	0⁽¹²⁾		1⁽¹⁵⁾		0⁽⁷⁾	0⁽¹⁰⁾
12	37	38	49	38	22	10	13
			1⁽¹⁾
28	21	48	43	44	29	26	12
		1⁽⁴⁾
37	22	39	46	26	20	44	49
							1⁽²⁾
22	49	19	2	20	30	45	16
	1⁽³⁾
45	27	5	21	30	21	34	23
1⁽⁶⁾
43	33	20	29	3	46	33	21
					1⁽⁵⁾

Суммарная эффективность, отвечающая полученному варианту выбора равна:

условных единиц эффективности

Вариант выбора проверим на оптимальность. Для этого вычислим потенциалы и оценки.

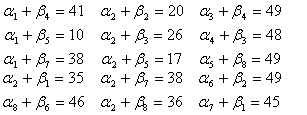
Отсюда вычислим потенциалы:

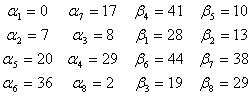
Для небазисных переменных вычислим оценки по соответствующей формуле:

И так далее расчеты по соответствующим формулам и данным приведены в таблице 5.2.

Таблица 5.2

Х₀	28	13	19	41	10	44	38	29
	31	13	11	41	10	17	38	25
0				0⁽⁷⁾	0⁽¹³⁾		1⁽⁸⁾
Оценка1	-3	0	8			27		4
	35	20	26	8	17	14	38	36
7	0⁽¹¹⁾	0⁽¹⁴⁾	0⁽¹²⁾		1⁽¹⁵⁾		0⁽⁷⁾	0⁽¹⁰⁾
Оценка2				40		37
8	12	37	38	49	38	22	10	13
				1⁽¹⁾
Оценка3	24	-16	-11		-20	30	36	24
29	28	21	48	43	44	29	26	12
			1⁽⁴⁾
Оценка4	29	21		27	-5	44	41	46
	37	22	39	46	26	20	44	49
20								1⁽²⁾
Оценка5	11	11	0	15	4	44	14
	22	49	19	2	20	30	45	16
36		1⁽³⁾
Оценка6	42		36	75	26	50	29	49
	45	27	5	21	30	21	34	23
17	1⁽⁶⁾
Оценка7		3	31	37	-3	40	21	23
	43	33	20	29	3	46	33	21
2						1⁽⁵⁾
Оценка8	-6	-11	8	-19	16		7	17

Cреди вычисленных оценок имеются отрицательные, это означает, что выбранный вариант назначения не является оптимальным. Наименьшая из отрицательных оценок Строим цикл пересчета: (3,5), (2,5), (1,7), (1,4), (3,5) замыкающийся на разрешающей клетке. Вычислим величину корректировки . Базисный нуль 0_3,5 перемещается в клетку (1,7), переменная х_1,7 включается в базис, а переменная х_3,5 выходит из базиса. Получим новую комбинацию расстановки единиц и нулей (Табл. 5.3). Суммарная эффективность равна:

условных единиц эффективности

Таблица 5.3

Х₀	28	13	19	41	10	44	38	29
	31	13	11	41	10	17	38	25
0				1⁽⁷⁾	0⁽¹³⁾		0⁽⁸⁾
Оценка1	-3	0	8			27		4
	35	20	26	8	17	14	38	36
7	0⁽¹¹⁾	0⁽¹⁴⁾	0⁽¹²⁾		0⁽¹⁵⁾		1⁽⁷⁾	0⁽¹⁰⁾
Оценка2				40		37
28	12	37	38	49	38	22	10	13
					1⁽⁷⁾
Оценка3	44	4	9	20		50	56	44
29	28	21	48	43	44	29	26	12
			1⁽⁴⁾
Оценка4	29	21		27	-5	44	41	46
	37	22	39	46	26	20	44	49
20								1⁽²⁾
Оценка5	11	11	0	15	4	44	14
	22	49	19	2	20	30	45	16
36		1⁽³⁾
Оценка6	42		36	75	26	50	29	49
	45	27	5	21	30	21	34	23
17	1⁽⁶⁾
Оценка7		3	31	37	-3	40	21	23
	43	33	20	29	3	46	33	21
2						1⁽⁵⁾
Оценка8	-6	-11	8	-19	16		7	17

Заново вычисляем потенциалы и оценки.

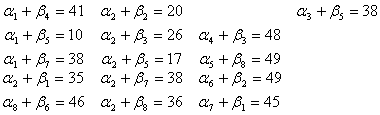
Отсюда вычислим потенциалы:

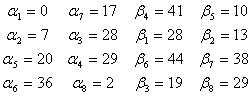
Для небазисных переменных вычислим оценки в таблице 5.3.

Среди вычисленных оценок имеются отрицательные, это означает, что выбранный вариант назначения не является оптимальным. Наименьшая из отрицательных оценок Строим цикл пересчета: (8,4), (2,4), (2,2), (8,2),(8,4) замыкающийся на разрешающей клетке. Вычислим величину корректировки . Базисная переменная х_2,2=0 перемещается в клетку (8,4), переменная х_8,4 включается в базис, а переменная х_2,2 выходит из базиса. (Табл. 5.4).

Таблица 5.4

Х₁	28	13	19	41	10	44	38	29
	31	13	11	41	10	17	38	25
0				1⁽⁷⁾	0⁽¹³⁾		0⁽⁸⁾
Оценка1	-3	0	8			27		4
	35	20	26	8	17	14	38	36
7	0⁽¹¹⁾		0⁽¹²⁾		0⁽¹⁵⁾		1⁽⁷⁾	0⁽¹⁰⁾
Оценка2				40		37
28	12	37	38	49	38	22	10	13
					1⁽⁷⁾
Оценка3	44	4	9	20		50	56	44
29	28	21	48	43	44	29	26	12
			1⁽⁴⁾
Оценка4	29	21		27	-5	44	41	46
	37	22	39	46	26	20	44	49
20								1⁽²⁾
Оценка5	11	11	0	15	4	44	14
	22	49	19	2	20	30	45	16
36		1⁽³⁾
Оценка6	42		36	75	26	50	29	49
	45	27	5	21	30	21	34	23
17	1⁽⁶⁾
Оценка7		3	31	37	-3	40	21	23
	43	33	20	29	3	46	33	21
2				0⁽¹⁴⁾		1⁽⁵⁾
Оценка8	-6	-11	8	-19	16		7	17

Суммарная эффективность не изменилась и равна:

условных единиц эффективности

Заново вычисляем потенциалы и оценки. Расчеты оценок приведены в таблице 5.5.

Среди вычисленных оценок имеются отрицательные, это означает, что выбранный вариант назначения не является оптимальным. Наименьшая из отрицательных оценок Строим цикл пересчета: (2,4), (2,5), (5,5), (5,2),(2,2) замыкающийся на разрешающей клетке. Вычислим величину корректировки . Базисная переменная х_5,2=0 перемещается в клетку (2,4), переменная х_2,4 включается в базис, а переменная х_5,2 выходит из базиса. (Табл. 5.5).

Таблица 5.5

Х₂	28	13	19	41	10	44	38	29
	31	13	11	41	10	17	38	25
0				1⁽⁷⁾	0⁽¹³⁾		0⁽⁸⁾
Оценка1	-3	0	8			27		4
	35	20	26	8	17	14	38	36
7	0⁽¹¹⁾		0⁽¹²⁾		0⁽¹⁵⁾		1⁽⁷⁾	0⁽¹⁰⁾
Оценка2				40		37
28	12	37	38	49	38	22	10	13
					1⁽⁷⁾
Оценка3	44	4	9	20		50	56	44
29	28	21	48	43	44	29	26	12
			1⁽⁴⁾
Оценка4	29	21		27	-5	44	41	46
	37	22	39	46	26	20	44	49
20								1⁽²⁾
Оценка5	11	11	0	15	4	44	14
	22	49	19	2	20	30	45	16
36		1⁽³⁾
Оценка6	42		36	75	26	50	29	49
	45	27	5	21	30	21	34	23
17	1⁽⁶⁾
Оценка7		3	31	37	-3	40	21	23
	43	33	20	29	3	46	33	21
21				0⁽¹⁴⁾		1⁽⁵⁾
Оценка8	6	11	20		29		26	29

Заново вычисляем потенциалы и оценки. Расчеты оценок приведены в таблице 5.5.

Отрицательных оценок нет. Назначение Х₂ оптимально, обозначим его через Х₂^*.

Суммарная эффективность, отвечающая полученному варианту назначения равна:

условных единиц эффективности

Назначение Х₂ оптимально. Итак, оптимальный вариант назначения имеет вид:

х_1,4=1 (первая невеста выберет четвертого жениха),

х_2,7=1 (вторая невеста выберет седьмого жениха),

х_3,5=1 (третья невеста выбрала пятого жениха),

х_4,3=1 (четвертая невеста выбрала третьего жениха),

х_5,8=1 (пятая невеста выберет восьмого жениха),

х_6,2=1 (шестая невеста выберет второго жениха),

х_7,1=1 (седьмая невеста выберет первого жениха),

х_8,6=1 (восьмая невеста выберет шестого жениха).

При этом варианте назначений получим максимальную эффективность единиц эффективности.

Метод Фогеля Читать далее: Венгерский метод

Раздел: Экономико-математическое моделирование
Количество знаков с пробелами: 38492
Количество таблиц: 36
Количество изображений: 26

Скачать

... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...

Скачать

... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...

Скачать

... продукции. Кроме того, т.к. объем ресурсов для оборудования дается в часах, а производительность оборудования в м¤/час, то необходимо перейти к соизмеримости. Таким образом, задача сводится к нахождению оптимального плана производства продукции каждого вида с целью получения максимальной прибыли. ЗЛП будет выглядеть так: Целевая функция: min Z = 0.51x1+0.57x2+0.13x3+0.33x4+0.38x5+0.72x6+0.23x7+0. ...

Скачать

... важной составной частью как денежного рынка, так и рынка капиталов, которые в совокупности составляют финансовый рынок. Цель функционирования рынка ценных бумаг -как и всех финансовых рынков - состоит в том, чтобы обеспечивать наличие механизма для привлечения инвестиций в экономику путем установления необходимых контактов между теми, кто нуждается в средствах, и теми, кто хотел бы инвестировать ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями