Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости
Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса
Проанализируем решение задачи, используя условия дополняющей нежесткости (вторую теорему двойственности)
Метод Фогеля
Метод потенциалов
Венгерский метод
Навигация
Метод Фогеля
Экономико-математический практикум
38492
знака
36
таблиц
26
изображений
3. Метод Фогеля
В табл. 3.4 показаны последовательность определения базисных переменных, наборы разностей 
в строках справа от таблицы, а 
в столбцах снизу под таблицей.
План Х0
Таблица 3.4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||||||
| 34 | 30 | 39 | 29 | 18 | 11 | 11 | 11 | 11 | 11 | 11 | - | - | ||
| 34(6) | 48(5) |
|
|
| 82 | |||||||||
|
| ||||||||||||||
| 40 | 35 | 45 | 41 | 10 |
| 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | |
| 14(7) |
| 22(8) |
|
| 36 | |||||||||
|
| ||||||||||||||
| 36 | 38 | 41 | 50 | 8 |
| 28 | 2 | - | - | - | - | - | - | |
| 29(2) |
|
|
| 50(1) | 79 | |||||||||
|
| ||||||||||||||
| 14 | 10 | 13 | 10 | 12 |
| 2 | 2 | 2 | 2 | - | - | - | - | |
| 12(4) |
| 68(3) |
| 80 | ||||||||||
| 77 | 60 | 22 | 68 | 50 | ||||||||||
| Этап 1 | 20 | 20 | 26 | 19 | 2 | |||||||||
| Этап 2 | 20 | 20 | 26 | 19 | - | |||||||||
| Этап 3 | 20 | 20 | 26 | 19 | - | |||||||||
| Этап 4 | 20 | 20 | 26 | 12 | - | |||||||||
| Этап 5 | 20 | - | 26 | - | - | |||||||||
| Этап 6 | 20 | - | 26 | - | - | |||||||||
| Этап 7 | 16 | - | 26 | - | - | |||||||||
| Этап 8 | - | - | 26 | - | - |
Суммарные транспортные расходы, соответствующие данному плану перевозок равны
.
Сравним расчеты, проделанные тремя методами. Транспортные расходы, рассчитанные:
1) методом северо-западного угла составили 8452 у.е.,
2) методом минимального элемента соответственно 6342 у.е.,
3) пересчитанные по методу потенциалов – 6118 у.е.,
4) методом Фогеля соответственно – 6390 у.е.
Наименьшие транспортные расходы составили расходы, рассчитанные по методу потенциалов.
Задача № 4
Сетевая задача
Ниже приведено 10 вариантов транспортной задачи в сетевой постановке. Каждая задача изображена в виде неориентированного связного графа. На ребрах проставлены значения тарифов 
, на вершинах (в кружках) — значения запасов-потребностей 
. Построить пробный допустимый план, проверить его на оптимальность. В случае необходимости довести до оптимального плана методом потенциалов.
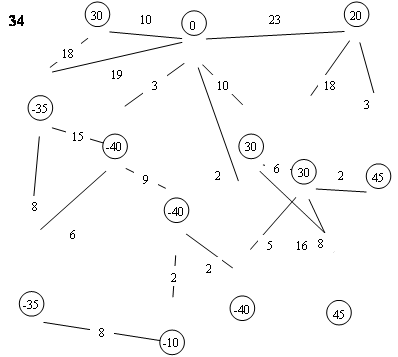
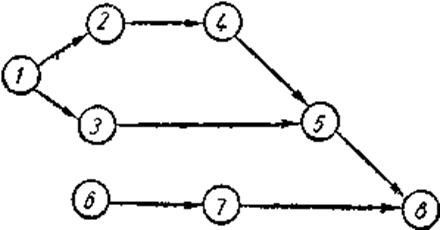
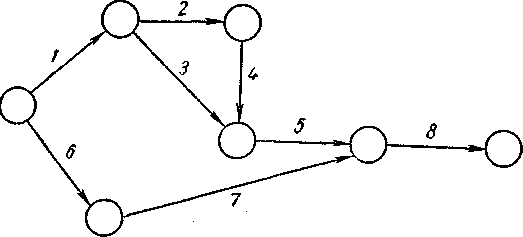
Решение. Построим пробный опорный план (рис.1).
 | |||||
 | |||||
 | |||||
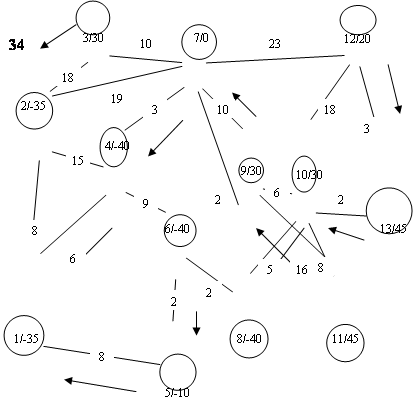Рис. 1. Пробный план перевозок по сети.
В качестве начальной выберем вершину 12, которая является поставщиком с запасами в 20 единиц продукции. Из этой вершины отправим транзитом через 13 с запасами 45 ед. и 10 вершину с запасами 30 единиц в 8 вершину и удовлетворяем её потребности в 40 единиц. Оставшиеся 55 единиц отправим в 6 вершину с потребностями 40 единиц, оставшиеся 15 единиц отправляем в 5 вершину с потребностями 10 единиц, оставшиеся 5 единиц направим в 1 вершину, потребности которой составляют 35 единиц.
Из 11 вершины с запасами 45 единиц направим транзитом через 9 вершину , всего запасов стало 75 единиц, направим их транзитом через 7 вершину в 4 вершину, потребности которой составляют 40 единиц, оставшиеся 35 единиц направим во 2 вершину и удовлетворим ее потребности.
Из 3 вершины с запасами 30 единиц направим транзитом через 7 вершину в 1 вершину, потребности которой удовлетворим.
В результате проведенных операций все запасы вывезены, потребности всех потребителей удовлетворены.
В результате проведенных операций все запасы вывезены, потребности всех потребителей удовлетворены. Число базисных ребер здесь равно 11, число вершин 13.
Итак, полученный план является опорным, так как удовлетворяет всем требованиям опорного плана. Значение функции, которое соответствует построенному плану равно
.
Проверку плана на оптимальность осуществим с помощью метода потенциалов.
Одной из вершин (например, 1) зададим произвольное значение потенциала α1=0. Запишем его около вершины 1.
Затем, двигаясь по базисным ребрам, вычисляем потенциалы остальных вершин.
; 
;
;
;
;
;
; 
;
После вычисления потенциалов находим оценки для небазисных ребер: (1,2), (2,4),(2,7), (3,7),(7,12), (7,8), (10,12),(4,6). Они определяются по формуле и равны соответственно:
;
;
;
;.
Есть три положительные оценки, значит построенный опорный план не оптимальный.
Наибольшая оценка 
. Ребро (7,8), объявляем разрешающим, направляем разрешающую стрелку (пока пустую) от вершины с меньшим потенциалом к вершине с большим потенциалом, т.е. от 7–й вершины к 8–й (на рис. 2 разрешающая стрелка намечена пунктиром). В результате получаем цикл пересчета, замыкающийся на ребре (7,8). Цикл пересчета на рис.2 намечен сплошной линией.
Рис.3. пересчет перевозок по потенциалам
Во второй строке выписываем ребра, принадлежащие циклу пересчета. В первой строке, над ребрами с помощью стрелок укажем направление перевозок, а в третьей строке – объем перевозимого груза. В четвертой строке полученной конструкции запишем 
, если направление перевозки совпадает с разрешающей стрелкой и 
, в противном случае.
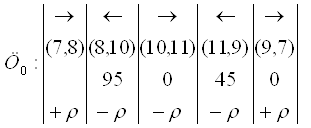
Изменяем распределение поставок. Определяем 
величину корректировки плана. Поскольку перевозки х8,10,х11,9 направлены против разрешающей стрелки, величина 
полагается меньшей из них 
Включаем в базис ребро (7,8), а объем перевозки полагаем равным величине корректировки 
Ребро (7,9) исключаем из базиса.
После пересчета получим значение функции:
Задача № 5
Задача о назначениях
Ниже приведены таблицы, в клетках которых проставлены элементы матрицы эффективностей 
задачи о разборчивой невесте. Решить задачу методом потенциалов и венгерским методом.
| 44 | ||||||||||
| 31 | 13 | 11 | 41 | 10 | 17 | 38 | 25 | |||
| 35 | 20 | 26 | 8 | 17 | 14 | 38 | 36 | |||
| 12 | 37 | 38 | 49 | 38 | 22 | 10 | 13 | |||
| 28 | 21 | 48 | 43 | 44 | 29 | 26 | 12 | |||
| 37 | 22 | 39 | 46 | 26 | 20 | 44 | 49 | |||
| 22 | 49 | 19 | 2 | 20 | 30 | 45 | 16 | |||
| 45 | 27 | 5 | 21 | 30 | 21 | 34 | 23 | |||
| 43 | 33 | 20 | 29 | 3 | 46 | 33 | 21 | |||
Решение.
Похожие работы
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
... продукции. Кроме того, т.к. объем ресурсов для оборудования дается в часах, а производительность оборудования в м¤/час, то необходимо перейти к соизмеримости. Таким образом, задача сводится к нахождению оптимального плана производства продукции каждого вида с целью получения максимальной прибыли. ЗЛП будет выглядеть так: Целевая функция: min Z = 0.51x1+0.57x2+0.13x3+0.33x4+0.38x5+0.72x6+0.23x7+0. ...
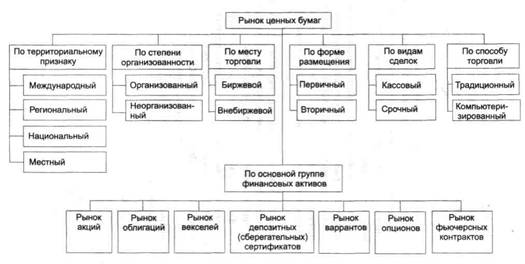
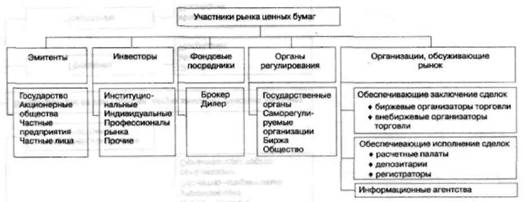
... важной составной частью как денежного рынка, так и рынка капиталов, которые в совокупности составляют финансовый рынок. Цель функционирования рынка ценных бумаг -как и всех финансовых рынков - состоит в том, чтобы обеспечивать наличие механизма для привлечения инвестиций в экономику путем установления необходимых контактов между теми, кто нуждается в средствах, и теми, кто хотел бы инвестировать ...
0 комментариев