Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости
Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса
Проанализируем решение задачи, используя условия дополняющей нежесткости (вторую теорему двойственности)
Метод Фогеля
Метод потенциалов
Венгерский метод
Навигация
Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса
Экономико-математический практикум
38492
знака
36
таблиц
26
изображений
2. Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса
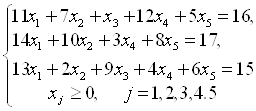
Составим расширенную задачу. В левые части уравнений системы ограничений вводим неотрицательные искусственные переменные с коэффициентом +1. Удобно справа от уравнений записать вводимые искусственные переменные. В первое уравнение вводим переменную х6, во второе — переменную х7, в третье – х8. Данная задача — задача на нахождение минимума. Получаем
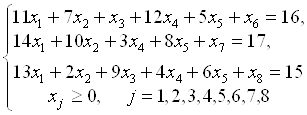
Данная расширенная задача имеет начальное опорное решение 
с базисом 
. Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении:
Записываем исходные и расчетные данные в симплексную таблицу (табл.2.2).
Таблица 2.2
| 1 | -5 | 6 | 8 | -2 | М | M | M | ||||
| Б | Сб | А0 | А1 | А2 | А3 | А4 | А5 | А6 | A7 | A8 | |
|
| А6 | М | 16 | 11 | 7 | 1 | 12 | 5 | 1 | 0 | 0 |
|
| A7 | M | 17 | 14 | 10 | 0 | 3 | 8 | 0 | 1 | 0 |
| ← | А8 | М | 15 | 13 | 2 | 9 | 4 | 6 | 0 | 0 | 1 |
|
|
| 0 | -1 | 5 | -6 | -8 | 2 | 0 | 0 | 0 | |
|
|
| 48 | 28 | 19 | 10 | 19 | 19 | 0 | 0 | 0 | |
Начальное опорное решение не является оптимальным, так как в задаче на минимум имеются положительные оценки. Выбираем номер вектора Аk, вводимого в базис опорного решения, и вектора Аl, выводимого из базиса. В столбце «А3» (см. табл. 2.1) за разрешающий элемент выбираем коэффициент 9 в третьей строке и выполняем преобразование Жордана.
Вектор А3 выводимый из базиса, исключаем из рассмотрения (вычеркиваем). Получаем первое опорное решение 
с базисом 
(табл. 2.3). Целевая функция 
=31,33М -10. Это решение не является оптимальным, так как имеются положительные оценки.
Таблица 2.3
| 1 | -5 | 6 | 8 | -2 | М | M | M | ||||
| Б | Сб | А0 | А1 | А2 | А3 | А4 | А5 | А6 | A7 | A8 | |
|
| А6 | М | 14,33 | 9,56 | 6,78 | 0,00 | 11,56 | 4,33 | 1,00 | 0,00 | -0,11 |
|
| A7 | M | 17,00 | 14,00 | 10,00 | 0,00 | 3,00 | 8,00 | 0,00 | 1,00 | 0,00 |
| ← | А3 | 6 | 1,67 | 1,44 | 0,22 | 1,00 | 0,44 | 0,67 | 0,00 | 0,00 | 0,11 |
|
|
| 10,00 | -7,67 | -6,33 | 0,00 | 5,33 | -6,00 | 0,00 | 0,00 | -0,67 | |
|
| 31,33 | 13,56 | 16,78 | 0,00 | 14,56 | 12,33 | 0,00 | 0,00 | -1,11 | ||
Вводим вектор А4 в базис, получаем второе опорное решение (таблица 2.4) 
с базисом 
. Целевая функция 
= 3,38+13,28M. Далее в таблице 2.4 приведены расчеты с третьей по пятую итерации.
Таблица 2.4
|
|
| 4 | 2 | -1 | 5 | 1 | М | M | M | ||
| Б | Сб | А0 | А1 | А2 | А3 | А4 | А5 | А6 | A7 | A8 | |
| a4 | 8 | 1,24 | 0,83 | 0,59 | 0,00 | 1,00 | 0,38 | 0,09 | 0,00 | -0,01 | |
| a7 | M | 13,28 | 11,52 | 8,24 | 0,00 | 0,00 | 6,88 | -0,26 | 1,00 | 0,03 | |
| a3 | 6 | 1,12 | 1,08 | -0,04 | 1,00 | 0,00 | 0,50 | -0,04 | 0,00 | 0,12 | |
|
| 3,38 | -12,08 | -9,46 | 0,00 | 0,00 | -8,00 | -0,46 | 0,00 | -0,62 | ||
| 13,28 | 1,52 | 8,24 | 0,00 | 0,00 | 6,88 | -1,26 | 0,00 | -0,97 | |||
| a4 | 8 | 0,52 | 0,20 | 0,14 | 0,00 | 1,00 | 0,00 | 0,10 | -0,05 | -0,01 | |
| a5 | -2 | 1,93 | 1,68 | 1,20 | 0,00 | 0,00 | 1,00 | -0,04 | 0,15 | 0,00 | |
| a3 | 6 | 0,15 | 0,24 | -0,64 | 1,00 | 0,00 | 0,00 | -0,02 | -0,07 | 0,11 | |
| 18,84 | 1,33 | 0,13 | 0,00 | 0,00 | 0,00 | -0,76 | 1,16 | -0,58 | |||
| 0,00 | -10,00 | 0,00 | 0,00 | 0,00 | 0,00 | -1,00 | -1,00 | -1,00 | |||
| a1 | 1 | 2,60 | 1,00 | 0,69 | 0,00 | 5,04 | 0,00 | 0,51 | -0,27 | -0,06 | |
| a5 | -2 | -2,42 | 0,00 | 0,04 | 0,00 | -8,44 | 1,00 | -0,89 | 0,61 | 0,10 | |
| a3 | 6 | -0,47 | 0,00 | -0,80 | 1,00 | -1,20 | 0,00 | -0,14 | -0,01 | 0,13 | |
| 4,19 | 0,00 | -0,79 | 0,00 | -6,68 | 0,00 | -1,44 | 1,53 | -0,51 | |||
| 25,99 | 0,00 | 6,90 | 0,00 | 50,35 | 0,00 | 4,07 | -3,75 | -1,56 | |||
Целевая функция после пятой итерации равна 
= 4,19. Положительных оценок нет, план оптимален. Ответ: min Z(X*) =4,2.
3.Построим двойственную задачу
Используя вторую симметричную пару двойственных задач, составим задачу, двойственную к исходной:
Вводим неотрицательные дополнительные переменные у4, у5, у6 у7, у8 для приведения задачи к каноническому виду:
Находим начальное опорное решение Y1 = (0,0,0,1,-5,6,8,-2) с базисом Б1 = (А4, А5, А6, А7, А8). Решение задачи симплексным методом приведено в табл. 2.5. (расчеты табл.2.2. и табл.2.4.)
Таблица 2.5
| 1 | -5 | 6 | 8 | -2 | М | M | M | ||||||
| Б | Сб | А0 | А1 | А2 | А3 | А4 | А5 | А6 | A7 | A8 | |||
| ← | А6 | М | 16 | 11 | 7 | 1 | 12 | 5 | 1 | 0 | 0 | ||
|
| A7 | M | 17 | 14 | 10 | 0 | 3 | 8 | 0 | 1 | 0 | ||
|
| А8 | М | 15 | 13 | 2 | 9 | 4 | 6 | 0 | 0 | 1 | ||
|
|
| 0 | -1 | 5 | -6 | -8 | 2 | 0 | 0 | 0 | |||
|
|
| 48 | 28 | 19 | 10 | 19 | 19 | 0 | 0 | 0 | |||
|
| a1 | 1 | 2,60 | 1,00 | 0,69 | 0,00 | 5,04 | 0,00 | 0,51 | -0,27 | -0,06 | ||
|
| a5 | -2 | -2,42 | 0,00 | 0,04 | 0,00 | -8,44 | 1,00 | -0,89 | 0,61 | 0,10 | ||
|
| a3 | 6 | -0,47 | 0,00 | -0,80 | 1,00 | -1,20 | 0,00 | -0,14 | -0,01 | 0,13 | ||
| 4,19 | 0,00 | -0,79 | 0,00 | -6,68 | 0,00 | -1,44 | 1,53 | -0,51 | ||||
|
| 25,99 | 0,00 | 6,90 | 0,00 | 50,35 | 0,00 | 4,07 | -3,75 | -1,56 | ||||
Приведем оптимальное решение прямой задачи
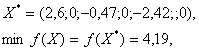
Окончательный базис, соответствующий оптимальному решению прямой задачи, состоит из векторов А2А3А4 поэтому базисная матрица имеет вид
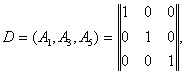
Решение прямой задачи начиналось с единичного базиса А6,А7,А8 . Поэтому в окончательной таблице указанные столбцы преобразуются в матрицу 
, обратную к базисной матрице 
, следовательно,
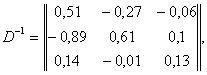
Оптимальный план двойственной найдем из соотношения
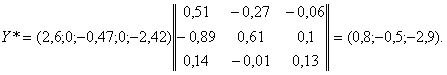
Откуда 
При этом плане максимальное значение функции двойственной задачи составляет величину равную
Максимальное значение целевой функции двойственной задачи совпадает с минимальным значением целевой функции прямой задачи.
Похожие работы
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
... того чтобы получить оптимальное решение нужно перейти на лист «Расчет» через основное меню, нажав кнопку «Расчеты». На листе «Расчет» представлена математическая модель оптимизации распределения трудовых ресурсов (рис 3.3) описанная в разделе 3.2. Данная модель использует надстройку «Поиск решений» MS Excel Рис 3.3. Для запуска надстройки «Поиск решений» MS Excel, необходимо в главном меню ...
... продукции. Кроме того, т.к. объем ресурсов для оборудования дается в часах, а производительность оборудования в м¤/час, то необходимо перейти к соизмеримости. Таким образом, задача сводится к нахождению оптимального плана производства продукции каждого вида с целью получения максимальной прибыли. ЗЛП будет выглядеть так: Целевая функция: min Z = 0.51x1+0.57x2+0.13x3+0.33x4+0.38x5+0.72x6+0.23x7+0. ...
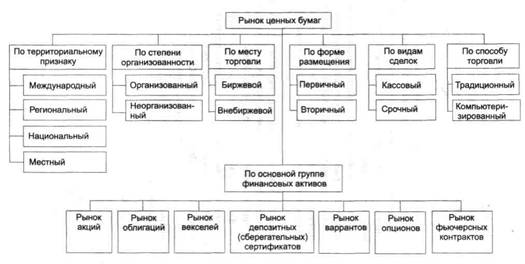
... важной составной частью как денежного рынка, так и рынка капиталов, которые в совокупности составляют финансовый рынок. Цель функционирования рынка ценных бумаг -как и всех финансовых рынков - состоит в том, чтобы обеспечивать наличие механизма для привлечения инвестиций в экономику путем установления необходимых контактов между теми, кто нуждается в средствах, и теми, кто хотел бы инвестировать ...
0 комментариев